Models#
Qibo provides models for both the circuit based and the adiabatic quantum
computation paradigms. Circuit based models include Circuit models which
allow defining arbitrary circuits and Quantum Fourier Transform (QFT) such as the
Quantum Fourier Transform (qibo.models.QFT) and the
Variational Quantum Eigensolver (qibo.models.VQE).
Adiabatic quantum computation is simulated using the Time evolution
of state vectors.
In order to perform calculations and apply gates to a state vector a backend
has to be used. The backends are defined in qibo/backends.
Circuit and gate objects are backend independent and can be executed with
any of the available backends.
Qibo uses big-endian byte order, which means that the most significant qubit is the one with index 0, while the least significant qubit is the one with the highest index.
Circuit models#
Circuit#
- class qibo.models.circuit.Circuit(nqubits: int | list | None = None, accelerators=None, density_matrix: bool = False, wire_names: list | None = None)[source]#
Circuit object which holds a list of gates.
This circuit is symbolic and cannot perform calculations. A specific backend has to be used for performing calculations.
Circuits can be created with a specific number of qubits and wire names.
Either
nqubitsorwire_namesmust be provided.If only
nqubitsis provided, wire names will default to[0, 1, ..., nqubits - 1].If only
wire_namesis provided,nqubitswill be set to the length ofwire_names.nqubitsandwire_namesmust be consistent with each other.
Example:
from qibo import Circuit # Every circuit initialization below is valid circuit = Circuit(5) # Default wire names are [0, 1, 2, 3, 4] circuit = Circuit(["A", "B", "C", "D", "E"]) circuit = Circuit(5, wire_names=["A", "B", "C", "D", "E"]) circuit = Circuit(wire_names=["A", "B", "C", "D", "E"])
- Parameters:
nqubits (int | list, optional) – Number of qubits in the circuit or a list of wire names.
wire_names (list, optional) – List of wire names
init_kwargs (dict) –
a dictionary with the following keys
nqubits
accelerators
density_matrix
wire_names.
queue (_Queue) – List that holds the queue of gates of a circuit.
parametrized_gates (_ParametrizedGates) – List of parametric gates.
trainable_gates (_ParametrizedGates) – List of trainable gates.
measurements (list) – List of non-collapsible measurements.
_final_state – Final result after full simulation of the circuit.
compiled (CompiledExecutor) – Circuit executor. Defaults to
None.repeated_execution (bool) – If True, the circuit would be re-executed when sampling. Defaults to
False.density_matrix (bool, optional) – If True, the circuit would evolve density matrices. If
False, defaults to statevector simulation. Defaults toFalse.accelerators (dict, optional) – Dictionary that maps device names to the number of times each device will be used. Defaults to
None.ndevices (int) – Total number of devices. Defaults to
None.nglobal (int) – Base two logarithm of the number of devices. Defaults to
None.nlocal (int) – Total number of available qubits in each device. Defaults to
None.queues (DistributedQueues) – Gate queues for each accelerator device. Defaults to
None.
- on_qubits(*qubits)[source]#
Generator of gates contained in the circuit acting on specified qubits.
Useful for adding a circuit as a subroutine in a larger circuit.
- Parameters:
qubits (int) – Qubit ids that the gates should act.
Example
from qibo import Circuit, gates # create small circuit on 4 qubits small_circuit = Circuit(4) small_circuit.add(gates.RX(i, theta=0.1) for i in range(4)) small_circuit.add((gates.CNOT(0, 1), gates.CNOT(2, 3))) # create large circuit on 8 qubits large_circuit = Circuit(8) large_circuit.add(gates.RY(i, theta=0.1) for i in range(8)) # add the small circuit to the even qubits of the large one large_circuit.add(small_circuit.on_qubits(*range(0, 8, 2)))
- light_cone(*qubits)[source]#
Reduces circuit to the qubits relevant for an observable.
Useful for calculating expectation values of local observables without requiring simulation of large circuits. Uses the light cone construction described in issue #571.
- Parameters:
qubits (int) – Qubit ids that the observable has support on.
- Returns:
- Circuit that contains only
the qubits that are required for calculating expectation involving the given observable qubits.
- qubit_map (dict): Dictionary mapping the qubit ids of the original
circuit to the ids in the new one.
- Return type:
circuit (
qibo.models.Circuit)
- copy(deep: bool = False)[source]#
Creates a copy of the current
circuitas a newCircuitmodel.- Parameters:
deep (bool) – If
Truecopies of the gate objects will be created for the new circuit. IfFalse, the same gate objects ofcircuitwill be used.- Returns:
The copied circuit object.
- invert()[source]#
Creates a new
Circuitthat is the inverse of the original.Inversion is obtained by taking the dagger of all gates in reverse order. If the original circuit contains parametrized gates, dagger will change their parameters. This action is not persistent, so if the parameters are updated afterwards, for example using
qibo.models.circuit.Circuit.set_parameters(), the action of dagger will be overwritten. If the original circuit contains measurement gates, these are included in the inverted circuit.- Returns:
Circuit corresponding to the inverse of the original
circuit.- Return type:
qibo.models.Circuit
- decompose(*free: int)[source]#
Decomposes circuit’s gates to gates supported by OpenQASM.
- Parameters:
free – Ids of free (work) qubits to use for gate decomposition.
- Returns:
Circuit that contains only gates that are supported by OpenQASM and has the same effect as the original circuit.
- with_pauli_noise(noise_map: Tuple[int, int, int] | Dict[int, Tuple[int, int, int]])[source]#
Creates a copy of the circuit with Pauli noise gates after each gate.
If the original circuit uses state vectors then noise simulation will be done using sampling and repeated circuit execution. In order to use density matrices the original circuit should be created setting the flag
density_matrix=True. For more information we refer to the How to perform noisy simulation? example.- Parameters:
noise_map (dict) – list of tuples \((P_{k}, p_{k})\), where \(P_{k}\) is a
strrepresenting the \(k\)-th \(n\)-qubit Pauli operator, and \(p_{k}\) is the associated probability.- Returns:
Circuit object that contains all the gates of the original circuit and additional noise channels on all qubits after every gate.
Example
from qibo import Circuit, gates # use density matrices for noise simulation circuit = Circuit(2, density_matrix=True) circuit.add([gates.H(0), gates.H(1), gates.CNOT(0, 1)]) noise_map = { 0: list(zip(["X", "Z"], [0.1, 0.2])), 1: list(zip(["Y", "Z"], [0.2, 0.1])) } noisy_circuit = circuit.with_pauli_noise(noise_map) # ``noisy_circuit`` will be equivalent to the following circuit circuit_2 = Circuit(2, density_matrix=True) circuit_2.add(gates.H(0)) circuit_2.add(gates.PauliNoiseChannel(0, [("X", 0.1), ("Z", 0.2)])) circuit_2.add(gates.H(1)) circuit_2.add(gates.PauliNoiseChannel(1, [("Y", 0.2), ("Z", 0.1)])) circuit_2.add(gates.CNOT(0, 1)) circuit_2.add(gates.PauliNoiseChannel(0, [("X", 0.1), ("Z", 0.2)])) circuit_2.add(gates.PauliNoiseChannel(1, [("Y", 0.2), ("Z", 0.1)]))
- add(gate)[source]#
Add a gate to a given queue.
- Parameters:
gate (
qibo.gates.Gate) – the gate object to add. See Gates for a list of available gates. gate can also be an iterable or generator of gates. In this case all gates in the iterable will be added in the circuit.- Returns:
If the circuit contains measurement gates with
collapse=Trueasympy.Symbolthat parametrizes the corresponding outcome.
- property measurement_tuples#
used for testing only
- gates_of_type(gate: str | type) List[Tuple[int, Gate]][source]#
Finds all gate objects of specific type or name.
This method can be affected by how
qibo.gates.Gate.controlled_by()behaves with certain gates. To see howqibo.gates.Gate.controlled_by()affects gates, we refer to the documentation ofqibo.gates.Gate.controlled_by().
- set_parameters(parameters)[source]#
Updates the parameters of the circuit’s parametrized gates.
For more information on how to use this method we refer to the How to use parametrized gates? example.
- Parameters:
parameters – Container holding the new parameter values. It can have one of the following types: List with length equal to the number of parametrized gates and each of its elements compatible with the corresponding gate. Dictionary with keys that are references to the parametrized gates and values that correspond to the new parameters for each gate. Flat list with length equal to the total number of free parameters in the circuit. A backend supported tensor (for example
np.ndarrayortf.Tensor) may also be given instead of a flat list.
Example
from qibo import Circuit, gates # create a circuit with all parameters set to 0. circuit = Circuit(3) circuit.add(gates.RX(0, theta=0)) circuit.add(gates.RY(1, theta=0)) circuit.add(gates.CZ(1, 2)) circuit.add(gates.fSim(0, 2, theta=0, phi=0)) circuit.add(gates.H(2)) # set new values to the circuit's parameters using list params = [0.123, 0.456, (0.789, 0.321)] circuit.set_parameters(params) # or using dictionary params = { circuit.queue[0]: 0.123, circuit.queue[1]: 0.456, circuit.queue[3]: (0.789, 0.321) } circuit.set_parameters(params) # or using flat list (or an equivalent `np.array`/`tf.Tensor`/`torch.Tensor`) params = [0.123, 0.456, 0.789, 0.321] circuit.set_parameters(params)
- get_parameters(output_format: str = 'list', include_not_trainable: bool = False) List | Dict[source]#
Returns the parameters of all parametrized gates in the circuit.
Inverse method of
qibo.models.circuit.Circuit.set_parameters().- Parameters:
output_format (str) – Format to return the variational parameters. Available formats are
"list","dict"and"flatlist". Seeqibo.models.circuit.Circuit.set_parameters()for more details on each format. Default is"list".include_not_trainable (bool) – If
Trueit includes the parameters of non-trainable parametrized gates in the returned list or dictionary. Default isFalse.
- associate_gates_with_parameters()[source]#
Associates to each parameter its gate.
- Returns:
A nparams-long flatlist whose i-th element is the gate parameterized by the i-th parameter.
- summary() str[source]#
Generates a summary of the circuit.
The summary contains the circuit depths, total number of qubits and the all gates sorted in decreasing number of appearance.
Example
from qibo import Circuit, gates circuit = Circuit(3) circuit.add(gates.H(0)) circuit.add(gates.H(1)) circuit.add(gates.CNOT(0, 2)) circuit.add(gates.CNOT(1, 2)) circuit.add(gates.H(2)) circuit.add(gates.TOFFOLI(0, 1, 2)) print(circuit.summary()) # Prints ''' Circuit depth = 5 Total number of gates = 6 Number of qubits = 3 Most common gates: h: 3 cx: 2 ccx: 1 '''
- fuse(max_qubits=2)[source]#
Creates an equivalent circuit by fusing gates for increased simulation performance.
- Parameters:
max_qubits (int) – Maximum number of qubits in the fused gates.
- Returns:
A
qibo.core.circuit.Circuitobject containingqibo.gates.FusedGategates, each of which corresponds to a group of some original gates. For more details on the fusion algorithm we refer to the Circuit fusion section.
Example
from qibo import Circuit, gates circuit = Circuit(2) circuit.add([gates.H(0), gates.H(1)]) circuit.add(gates.CNOT(0, 1)) circuit.add([gates.Y(0), gates.Y(1)]) # create circuit with fused gates fused_circuit = circuit.fuse() # now ``fused_circuit`` contains a single ``FusedGate`` that is # equivalent to applying the five original gates
- unitary(backend=None)[source]#
Creates the unitary matrix corresponding to all circuit gates.
This is a \(2^{n} \times 2^{n}`\) matrix obtained by multiplying all circuit gates, where \(n\) is
nqubits.
- property final_state#
Returns the final state after full simulation of the circuit.
If the circuit is executed more than once, only the last final state is returned.
- execute(initial_state=None, nshots: int = 1000, **kwargs)[source]#
Executes the circuit. Exact implementation depends on the backend.
- Parameters:
initial_state (ndarray or
qibo.models.circuit.Circuit) – Initial configuration. It can be specified by the setting the state vector using an array or a circuit. IfNone, the initial state is|000..00>.nshots (int, optional) – Number of shots. Defaults ot \(1000\).
- Returns:
Either a
qibo.result.QuantumState,qibo.result.MeasurementOutcomesorqibo.result.CircuitResultdepending on the circuit’s configuration.
- to_qasm(extended_compatibility: bool = False)[source]#
Convert circuit to a QASM string.
- Parameters:
extended_compatibility (bool) – if
True, unrolls more exotic gates in their decomposition by defining them as custom gates, this increases the compatibility with other frameworks, such as qiskit. Defaults toFalse.- Returns:
(str) the generated QASM.
Note
This method does not support multi-controlled gates and gates with
torch.Tensoras parameters.
- classmethod from_qasm(qasm_code, **circuit_kwargs)[source]#
Constructs a circuit from QASM code.
- Parameters:
qasm_code (str) – String with the QASM script.
- Returns:
A
qibo.models.circuit.Circuitthat contains the gates specified by the given QASM script.
Example
from qibo import Circuit, gates qasm_code = '''OPENQASM 2.0; include "qelib1.inc"; qreg q[2]; h q[0]; h q[1]; cx q[0],q[1];''' circuit = Circuit.from_qasm(qasm_code) # is equivalent to creating the following circuit circuit_2 = Circuit(2) circuit_2.add(gates.H(0)) circuit_2.add(gates.H(1)) circuit_2.add(gates.CNOT(0, 1))
- to_qir()[source]#
Convert circuit to QIR circuit.
Uses qbraid (https://github.com/qBraid/qBraid) to transpile the circuit into pyqir circuits.
- to_cudaq()[source]#
Convert circuit to CUDA-Q (quake) code.
Uses qbraid (https://github.com/qBraid/qBraid) to transpile the circuit into cudaq circuits.
- classmethod from_cudaq(cudaq_circuit_code)[source]#
Construct a circuit from CUDA-Q (quake) code.
Uses qbraid (https://github.com/qBraid/qBraid) to transpile the cudaq circuit into a qibo.models.circuit.Circuit.
- Parameters:
cudaq_circuit_code (PyKernel) – kernel containing the cudaq circuit code.
- Returns:
qibo.models.circuit.Circuitrepresenting the given circuit.
- diagram(line_wrap: int = 70, legend: bool = False) str[source]#
Build the string representation of the circuit diagram.
Circuit addition#
qibo.models.circuit.Circuit objects support addition. For example
circuit_1 = QFT(4)
circuit_2 = Circuit(4)
circuit_2.add(gates.RZ(0, 0.1234))
circuit_2.add(gates.RZ(1, 0.1234))
circuit_2.add(gates.RZ(2, 0.1234))
circuit_2.add(gates.RZ(3, 0.1234))
circuit = circuit_1 + circuit_2
will create a circuit that performs the Quantum Fourier Transform on four qubits followed by Rotation-Z gates.
Circuit fusion#
The gates contained in a circuit can be fused up to two-qubits using the
qibo.models.circuit.Circuit.fuse() method. This returns a new circuit
for which the total number of gates is less than the gates in the original
circuit as groups of gates have been fused to a single
qibo.gates.special.FusedGate gate. Simulating the new circuit
is equivalent to simulating the original one but in most cases more efficient
since less gates need to be applied to the state vector.
The fusion algorithm works as follows: First all gates in the circuit are
transformed to unmarked qibo.gates.special.FusedGate. The gates
are then processed in the order they were added in the circuit. For each gate
we identify the neighbors forth and back in time and attempt to fuse them to
the gate. Two gates can be fused if their total number of target qubits is
smaller than the fusion maximum qubits (specified by the user) and there are
no other gates between acting on the same target qubits. Gates that are fused
to others are marked. The new circuit queue contains the gates that remain
unmarked after the above operations finish.
Gates are processed in the original order given by user. There are no
additional simplifications performed such as commuting gates acting on the same
qubit or canceling gates even when such simplifications are mathematically possible.
The user can specify the maximum number of qubits in a fused gate using
the max_qubits flag in qibo.models.circuit.Circuit.fuse().
For example the following:
from qibo import Circuit, gates
circuit = Circuit(2)
circuit.add([gates.H(0), gates.H(1)])
circuit.add(gates.CZ(0, 1))
circuit.add([gates.X(0), gates.Y(1)])
fused_circuit = circuit.fuse()
will create a new circuit with a single qibo.gates.special.FusedGate
acting on (0, 1), while the following:
from qibo import Circuit, gates
circuit = Circuit(3)
circuit.add([gates.H(0), gates.H(1), gates.H(2)])
circuit.add(gates.CZ(0, 1))
circuit.add([gates.X(0), gates.Y(1), gates.Z(2)])
circuit.add(gates.CNOT(1, 2))
circuit.add([gates.H(0), gates.H(1), gates.H(2)])
fused_circuit = circuit.fuse()
will give a circuit with two fused gates, the first of which will act on
(0, 1) corresponding to
[H(0), H(1), CZ(0, 1), X(0), H(0)]
and the second will act to (1, 2) corresponding to
[Y(1), Z(2), CNOT(1, 2), H(1), H(2)]
Quantum Fourier Transform (QFT)#
- class qibo.models.qft.QFT(nqubits: int, with_swaps: bool = True, accelerators=None, **kwargs)[source]#
Creates a circuit that implements the Quantum Fourier Transform.
- Parameters:
nqubits (int) – number of qubits in the circuit.
with_swaps (bool, optional) – If
True, usesqibo.gates.SWAPgates at the end of the circuit so that the qubit order in the final state is the same as the initial state. Defauts toTrue.accelerators (dict, optional) – Accelerator device dictionary in order to use a distributed circuit. If
None, a simple (non-distributed) circuit will be used.kwargs (dict, optional) – Additional arguments used to initialize
qibo.models.Circuit. For details, see the documentation ofqibo.models.circuit.Circuit.
- Returns:
implementation of the Quantum Fourier Transform.
- Return type:
qibo.models.Circuit
Example
import numpy as np from qibo.models import QFT nqubits = 6 circuit = QFT(nqubits) # Random normalized initial state vector init_state = np.random.random(2 ** nqubits) + 1j * np.random.random(2 ** nqubits) init_state = init_state / np.sqrt((np.abs(init_state)**2).sum()) # Execute the circuit final_state = circuit(init_state)
Variational Quantum Eigensolver (VQE)#
- class qibo.models.variational.VQE(circuit, hamiltonian)[source]#
This class implements the variational quantum eigensolver algorithm.
- Parameters:
circuit (
qibo.models.circuit.Circuit) – Circuit that implements the variaional ansatz.hamiltonian (
qibo.hamiltonians.Hamiltonian) – Hamiltonian object.
Example
import numpy as np from qibo import Circuit, gates from qibo.hamiltonians import XXZ from qibo.models import VQE # create circuit ansatz for two qubits circuit = Circuit(2) circuit.add(gates.RY(0, theta=0)) # create XXZ Hamiltonian for two qubits hamiltonian = XXZ(2) # create VQE model for the circuit and Hamiltonian vqe = VQE(circuit, hamiltonian) # optimize using random initial variational parameters initial_parameters = np.random.uniform(0, 2, 1) vqe.minimize(initial_parameters)
- minimize(initial_state, method='Powell', loss_func=None, jac=None, hess=None, hessp=None, bounds=None, constraints=(), tol=None, callback=None, options=None, compile=False, processes=None)[source]#
Search for parameters which minimizes the hamiltonian expectation.
- Parameters:
initial_state (array) – a initial guess for the parameters of the variational circuit.
method (str) – the desired minimization method. See
qibo.optimizers.optimize()for available optimization methods.loss (callable) – loss function, the default one is
qibo.models.utils.vqe_loss().jac (dict) – Method for computing the gradient vector for scipy optimizers.
hess (dict) – Method for computing the hessian matrix for scipy optimizers.
hessp (callable) – Hessian of objective function times an arbitrary vector for scipy optimizers.
bounds (sequence or Bounds) – Bounds on variables for scipy optimizers.
constraints (dict) – Constraints definition for scipy optimizers.
tol (float) – Tolerance of termination for scipy optimizers.
callback (callable) – Called after each iteration for scipy optimizers.
options (dict) – a dictionary with options for the different optimizers.
compile (bool) – whether the TensorFlow graph should be compiled.
processes (int) – number of processes when using the paralle BFGS method.
- Returns:
The final expectation value. The corresponding best parameters. The optimization result object. For scipy methods it returns the
OptimizeResult, for'cma'theCMAEvolutionStrategy.result, and for'sgd'the options used during the optimization.
Adiabatically Assisted Variational Quantum Eigensolver (AAVQE)#
- class qibo.models.variational.AAVQE(circuit, easy_hamiltonian, problem_hamiltonian, s, nsteps=10, t_max=1, bounds_tolerance=1e-07, time_tolerance=1e-07)[source]#
This class implements the Adiabatically Assisted Variational Quantum Eigensolver algorithm. See https://arxiv.org/abs/1806.02287.
- Parameters:
circuit (
qibo.models.circuit.Circuit) – variational ansatz.easy_hamiltonian (
qibo.hamiltonians.Hamiltonian) – initial Hamiltonian object.problem_hamiltonian (
qibo.hamiltonians.Hamiltonian) – problem Hamiltonian object.s (callable) – scheduling function of time that defines the adiabatic evolution. It must verify boundary conditions: s(0) = 0 and s(1) = 1.
nsteps (float) – number of steps of the adiabatic evolution.
t_max (float) – total time evolution.
bounds_tolerance (float) – tolerance for checking s(0) = 0 and s(1) = 1.
time_tolerance (float) – tolerance for checking if time is greater than t_max.
Example
import numpy as np from qibo import Circuit, gates from qibo.hamiltonians import X, XXZ from qibo.models import AAVQE # create circuit ansatz for two qubits circuit = Circuit(2) circuit.add(gates.RY(0, theta=0)) circuit.add(gates.RY(1, theta=0)) # define the easy and the problem Hamiltonians. easy_hamiltonian = X(2) problem_hamiltonian = XXZ(2) # define a scheduling function with only one parameter # and boundary conditions s(0) = 0, s(1) = 1 s = lambda t: t # create AAVQE model aavqe = AAVQE( circuit, easy_hamiltonian, problem_hamiltonian, s, nsteps=10, t_max=1 ) # optimize using random initial variational parameters np.random.seed(0) initial_parameters = np.random.uniform(0, 2*np.pi, 2) ground_energy, params = aavqe.minimize(initial_parameters)
- minimize(params, method='BFGS', jac=None, hess=None, hessp=None, bounds=None, constraints=(), tol=None, options=None, compile=False, processes=None)[source]#
Performs minimization to find the ground state of the problem Hamiltonian.
- Parameters:
params (np.ndarray or list) – initial guess for the parameters of the variational circuit.
method (str) – optimizer to employ.
jac (dict) – Method for computing the gradient vector for scipy optimizers.
hess (dict) – Method for computing the hessian matrix for scipy optimizers.
hessp (callable) – Hessian of objective function times an arbitrary vector for scipy optimizers.
bounds (sequence or Bounds) – Bounds on variables for scipy optimizers.
constraints (dict) – Constraints definition for scipy optimizers.
tol (float) – Tolerance of termination for scipy optimizers.
options (dict) – a dictionary with options for the different optimizers.
compile (bool) – whether the TensorFlow graph should be compiled.
processes (int) – number of processes when using the parallel BFGS method.
Quantum Approximate Optimization Algorithm (QAOA)#
- class qibo.models.variational.QAOA(hamiltonian, mixer=None, solver='exp', callbacks=[], accelerators=None)[source]#
Quantum Approximate Optimization Algorithm (QAOA) model.
The QAOA is introduced in arXiv:1411.4028.
- Parameters:
hamiltonian (
qibo.hamiltonians.Hamiltonian) – problem Hamiltonian whose ground state is sought.mixer (
qibo.hamiltonians.Hamiltonian) – mixer Hamiltonian. Must be of the same type and act on the same number of qubits ashamiltonian. IfNone,qibo.hamiltonians.Xis used.solver (str) – solver used to apply the exponential operators. Default solver is ‘exp’ (
qibo.solvers.Exponential).callbacks (list) – List of callbacks to calculate during evolution.
accelerators (dict) – Dictionary of devices to use for distributed execution. This option is available only when
hamiltonianis aqibo.hamiltonians.SymbolicHamiltonian.
Example
import numpy as np from qibo import models, hamiltonians # create XXZ Hamiltonian for four qubits hamiltonian = hamiltonians.XXZ(4) # create QAOA model for this Hamiltonian qaoa = models.QAOA(hamiltonian) # optimize using random initial variational parameters # and default options and initial state initial_parameters = 0.01 * np.random.random(4) best_energy, final_parameters, extra = qaoa.minimize(initial_parameters, method="BFGS")
- set_parameters(p)[source]#
Sets the variational parameters.
- Parameters:
p (np.ndarray) – 1D-array holding the new values for the variational parameters. Length should be an even number.
- execute(initial_state=None)[source]#
Applies the QAOA exponential operators to a state.
- Parameters:
initial_state (np.ndarray) – Initial state vector.
- Returns:
State vector after applying the QAOA exponential gates.
- minimize(initial_p, initial_state=None, method='Powell', loss_func=None, loss_func_param={}, jac=None, hess=None, hessp=None, bounds=None, constraints=(), tol=None, callback=None, options=None, compile=False, processes=None)[source]#
Optimizes the variational parameters of the QAOA. A few loss functions are provided for QAOA optimizations such as expected value (default), CVar which is introduced in Quantum 4, 256, and Gibbs loss function which is introduced in PRR 2, 023074 (2020).
- Parameters:
initial_p (np.ndarray) – initial guess for the parameters.
initial_state (np.ndarray) – initial state vector of the QAOA.
method (str) – the desired minimization method. See
qibo.optimizers.optimize()for available optimization methods.loss_func (function) – the desired loss function. If it is None, the expectation is used.
loss_func_param (dict) – a dictionary to pass in the loss function parameters.
jac (dict) – Method for computing the gradient vector for scipy optimizers.
hess (dict) – Method for computing the hessian matrix for scipy optimizers.
hessp (callable) – Hessian of objective function times an arbitrary vector for scipy optimizers.
bounds (sequence or Bounds) – Bounds on variables for scipy optimizers.
constraints (dict) – Constraints definition for scipy optimizers.
tol (float) – Tolerance of termination for scipy optimizers.
callback (callable) – Called after each iteration for scipy optimizers.
options (dict) – a dictionary with options for the different optimizers.
compile (bool) – whether the TensorFlow graph should be compiled.
processes (int) – number of processes when using the paralle BFGS method.
- Returns:
The final energy (expectation value of the
hamiltonian). The corresponding best parameters. The optimization result object. For scipy methods it returns theOptimizeResult, for'cma'theCMAEvolutionStrategy.result, and for'sgd'the options used during the optimization.
Example
from qibo import hamiltonians from qibo.models.utils import cvar, gibbs h = hamiltonians.XXZ(3) qaoa = models.QAOA(h) initial_p = [0.314, 0.22, 0.05, 0.59] best, params, _ = qaoa.minimize(initial_p) best, params, _ = qaoa.minimize(initial_p, loss_func=cvar, loss_func_param={'alpha':0.1}) best, params, _ = qaoa.minimize(initial_p, loss_func=gibbs, loss_func_param={'eta':0.1})
Feedback-based Algorithm for Quantum Optimization (FALQON)#
- class qibo.models.variational.FALQON(hamiltonian, mixer=None, solver='exp', callbacks=[], accelerators=None)[source]#
Feedback-based ALgorithm for Quantum OptimizatioN (FALQON) model.
The FALQON is introduced in arXiv:2103.08619. It inherits the QAOA class.
- Parameters:
hamiltonian (
qibo.hamiltonians.Hamiltonian) – problem Hamiltonian whose ground state is sought.mixer (
qibo.hamiltonians.Hamiltonian) – mixer Hamiltonian. IfNone,qibo.hamiltonians.Xis used.solver (str) – solver used to apply the exponential operators. Default solver is ‘exp’ (
qibo.solvers.Exponential).callbacks (list) – List of callbacks to calculate during evolution.
accelerators (dict) – Dictionary of devices to use for distributed execution. This option is available only when
hamiltonianis aqibo.hamiltonians.SymbolicHamiltonian.
Example
import numpy as np from qibo import models, hamiltonians # create XXZ Hamiltonian for four qubits hamiltonian = hamiltonians.XXZ(4) # create FALQON model for this Hamiltonian falqon = models.FALQON(hamiltonian) # optimize using random initial variational parameters # and default options and initial state delta_t = 0.01 max_layers = 3 best_energy, final_parameters, extra = falqon.minimize(delta_t, max_layers)
- minimize(delta_t, max_layers, initial_state=None, tol=None, callback=None)[source]#
Optimizes the variational parameters of the FALQON.
- Parameters:
delta_t (float) – initial guess for the time step. A too large delta_t will make the algorithm fail.
max_layers (int) – maximum number of layers allowed for the FALQON.
initial_state (np.ndarray) – initial state vector of the FALQON.
tol (float) – Tolerance of energy change. If not specified, no check is done.
callback (callable) – Called after each iteration for scipy optimizers.
options (dict) – a dictionary with options for the different optimizers.
- Returns:
The final energy (expectation value of the
hamiltonian). The corresponding best parameters. extra: variable with historical data for the energy and callbacks.
Grover’s Algorithm#
- class qibo.models.grover.Grover(oracle, superposition_circuit=None, initial_state_circuit=None, superposition_qubits=None, superposition_size=None, number_solutions=None, target_amplitude=None, check=None, check_args=(), iterative=False)[source]#
Model that performs Grover’s algorithm.
For Grover’s original search algorithm: arXiv:quant-ph/9605043 For the iterative version with unknown solutions:arXiv:quant-ph/9605034 For the Grover algorithm with any superposition:arXiv:quant-ph/9712011
- Parameters:
oracle (
qibo.core.circuit.Circuit) – quantum circuit that flips the sign using a Grover ancilla initialized with -X-H-. Grover ancilla expected to be last qubit of oracle circuit.superposition_circuit (
qibo.core.circuit.Circuit) – quantum circuit that takes an initial state to a superposition. Expected to use the first set of qubits to store the relevant superposition.initial_state_circuit (
qibo.core.circuit.Circuit) – quantum circuit that initializes the state. If empty defaults to|000..00>superposition_qubits (int) – number of qubits that store the relevant superposition. Leave empty if superposition does not use ancillas.
superposition_size (int) – how many states are in a superposition. Leave empty if its an equal superposition of quantum states.
number_solutions (int) – number of expected solutions. Needed for normal Grover. Leave empty for iterative version.
target_amplitude (float) – absolute value of the amplitude of the target state. Only for advanced use and known systems.
check (function) – function that returns True if the solution has been found. Required of iterative approach. First argument should be the bitstring to check.
check_args (tuple) – arguments needed for the check function. The found bitstring not included.
iterative (bool) – force the use of the iterative Grover
Example
import numpy as np from qibo import Circuit, gates from qibo.models.grover import Grover # Create an oracle. Ex: Oracle that detects state |11111> oracle = Circuit(5 + 1) oracle.add(gates.X(5).controlled_by(*range(5))) # Create superoposition circuit. Ex: Full superposition over 5 qubits. superposition = Circuit(5) superposition.add([gates.H(i) for i in range(5)]) # Generate and execute Grover class grover = Grover(oracle, superposition_circuit=superposition, number_solutions=1) solution, iterations = grover()
- circuit(iterations)[source]#
Creates circuit that performs Grover’s algorithm with a set amount of iterations.
- Parameters:
iterations (int) – number of times to repeat the Grover step.
- Returns:
qibo.core.circuit.Circuitthat performs Grover’s algorithm.
- iterative_grover(lamda_value=1.2, backend=None)[source]#
Iterative approach of Grover for when the number of solutions is not known.
- Parameters:
lamda_value (real) – parameter that controls the evolution of the iterative method. Must be between 1 and 4/3.
backend (
qibo.backends.abstract.Backend) – Backend to use for circuit execution.
- Returns:
bitstring measured and checked as a valid solution. total_iterations (int): number of times the oracle has been called.
- Return type:
measured (str)
- execute(nshots=100, freq=False, logs=False, backend=None)[source]#
Execute Grover’s algorithm.
If the number of solutions is given, calculates iterations, otherwise it uses an iterative approach.
- Parameters:
nshots (int) – number of shots in order to get the frequencies.
freq (bool) – print the full frequencies after the exact Grover algorithm.
backend (
qibo.backends.abstract.Backend) – Backend to use for circuit execution.
- Returns:
bitstring (or list of bitstrings) measured as solution of the search. iterations (int): number of oracle calls done to reach a solution.
- Return type:
solution (str)
Travelling Salesman Problem#
- class qibo.models.tsp.TSP(distance_matrix, backend=None)[source]#
The travelling salesman problem (also called the travelling salesperson problem or TSP) asks the following question: “Given a list of cities and the distances between each pair of cities, what is the shortest possible route for a salesman to visit each city exactly once and return to the origin city?” It is an NP-hard problem in combinatorial optimization. It is also important in theoretical computer science and operations research.
This is a TSP class that enables us to implement TSP according to arxiv:1709.03489 by Hadfield (2017).
- Parameters:
distance_matrix – a numpy matrix encoding the distance matrix.
backend – Backend to use for calculations. If not given the global backend will be used.
Example
from qibo.models.tsp import TSP import numpy as np from collections import defaultdict from qibo import gates from qibo.models import QAOA from qibo.result import CircuitResult def convert_to_standard_Cauchy(config): m = int(np.sqrt(len(config))) cauchy = [-1] * m # Cauchy's notation for permutation, e.g. (1,2,0) or (2,0,1) for i in range(m): for j in range(m): if config[m * i + j] == '1': cauchy[j] = i # citi i is in slot j for i in range(m): if cauchy[i] == 0: cauchy = cauchy[i:] + cauchy[:i] return tuple(cauchy) # now, the cauchy notation for permutation begins with 0 def evaluate_dist(cauchy): ''' Given a permutation of 0 to n-1, we compute the distance of the tour ''' m = len(cauchy) return sum(distance_matrix[cauchy[i]][cauchy[(i+1)%m]] for i in range(m)) def qaoa_function_of_layer(layer, distance_matrix): ''' This is a function to study the impact of the number of layers on QAOA, it takes in the number of layers and compute the distance of the mode of the histogram obtained from QAOA ''' small_tsp = TSP(distance_matrix) obj_hamil, mixer = small_tsp.hamiltonians() qaoa = QAOA(obj_hamil, mixer=mixer) best_energy, final_parameters, extra = qaoa.minimize(initial_p=[0.1] * layer, initial_state=initial_state, method='BFGS') qaoa.set_parameters(final_parameters) quantum_state = qaoa.execute(initial_state) circuit = Circuit(9) circuit.add(gates.M(*range(9))) result = CircuitResult(quantum_state, circuit.measurements, small_tsp.backend, nshots=1000) freq_counter = result.frequencies() # let's combine freq_counter here, first convert each key and sum up the frequency cauchy_dict = defaultdict(int) for freq_key in freq_counter: standard_cauchy_key = convert_to_standard_Cauchy(freq_key) cauchy_dict[standard_cauchy_key] += freq_counter[freq_key] max_key = max(cauchy_dict, key=cauchy_dict.get) return evaluate_dist(max_key) np.random.seed(42) num_cities = 3 distance_matrix = np.array([[0, 0.9, 0.8], [0.4, 0, 0.1],[0, 0.7, 0]]) distance_matrix = distance_matrix.round(1) small_tsp = TSP(distance_matrix) initial_parameters = np.random.uniform(0, 1, 2) initial_state = small_tsp.prepare_initial_state([i for i in range(num_cities)]) qaoa_function_of_layer(2, distance_matrix)
Iterative Quantum Amplitude Estimation (IQAE)#
- class qibo.models.iqae.IQAE(circuit_a, circuit_q, alpha=0.05, epsilon=0.005, n_shots=1024, method='chernoff')[source]#
Model that performs the Iterative Quantum Amplitude Estimation algorithm.
The implemented class in this code utilizes the Iterative Quantum Amplitude Estimation (IQAE) algorithm, which was proposed in arxiv:1912.05559. The algorithm provides an estimated output that, with a probability
alpha, differs from the target value byepsilon. Bothalphaandepsiloncan be specified.Unlike Brassard’s original QAE algorithm arxiv:quant-ph/0005055, this implementation does not rely on Quantum Phase Estimation but instead is based solely on Grover’s algorithm. The IQAE algorithm employs a series of carefully selected Grover iterations to determine an estimate for the target amplitude.
- Parameters:
circuit_a (
qibo.models.circuit.Circuit) – quantum circuit that specifies the QAE problem.circuit_q (
qibo.models.circuit.Circuit) – quantum circuit of the Grover/Amplification operator.alpha (float) – confidence level, the target probability is 1 -
alpha, has values between 0 and 1.epsilon (float) – target precision for estimation target a, has values between 0 and 0.5.
method (str) – statistical method used to estimate the confidence intervals in each iteration, can be either chernoff (default) for the Chernoff intervals or beta for the Clopper-Pearson intervals.
n_shots (int) – number of shots.
- Raises:
ValueError – If
epsilonis not in (0, 0.5].ValueError – If
alphais not in (0, 1).ValueError – If
methodis not supported.ValueError – If the number of qubits in
circuit_ais greater than incircuit_q.
Example
from qibo import Circuit, gates from qibo.models.iqae import IQAE # Defining circuit A to integrate sin(x)^2 from [0,1] a_circuit = Circuit(2) a_circuit.add(gates.H(0)) a_circuit.add(gates.RY(q = 1, theta = 1 / 2)) a_circuit.add(gates.CU3(0, 1, 1, 0, 0)) # Defining circuit Q = -A S_0 A^-1 S_X q_circuit = Circuit(2) # S_X q_circuit.add(gates.Z(q = 1)) # A^-1 q_circuit = q_circuit + a_circuit.invert() # S_0 q_circuit.add(gates.X(0)) q_circuit.add(gates.X(1)) q_circuit.add(gates.CZ(0, 1)) # A q_circuit = q_circuit + a_circuit # Executing IQAE and obtaining the result iae = IQAE(a_circuit, q_circuit) results = iae.execute() integral_value = results.estimation integral_error = results.epsilon_estimated
- construct_qae_circuit(k)[source]#
Generates quantum circuit for QAE.
- Parameters:
k (int) – number of times the amplification operator
circuit_qis applied.- Returns:
The quantum circuit of the QAE algorithm.
- clopper_pearson(count, n, alpha)[source]#
Calculates the confidence interval for the quantity to estimate a.
- calc_L_range_CP(n_shots, upper_bound_t)[source]#
Calculate the confidence interval for the Clopper-Pearson method.
- calc_L_range_CH(n_shots, upper_bound_t)[source]#
Calculate the confidence interval for the Chernoff method.
- find_next_k(uppercase_k_i, up_i, theta_l, theta_u, r=2)[source]#
Find the largest integer
uppercase_ksuch that the intervaluppercase_k* [theta_l,theta_u] lies completely in [0, pi] or [pi, 2 pi].- Parameters:
uppercase_k_i (int) – the current
uppercase_ksuchuppercase_k= 4k+ 2, wherekis the power of the operatorcircuit_q.up_i (bool) – boolean flag of whether theta_interval lies in the upper half-circle [0, pi] or in the lower one [pi, 2 pi].
theta_l (float) – the current lower limit of the confidence interval for the angle theta.
theta_u (float) – the current upper limit of the confidence interval for the angle theta.
r (int) – lower bound for
uppercase_k.
- Returns:
The next power K_i, and boolean flag for the extrapolated interval.
- execute(backend=None)[source]#
Execute IQAE algorithm.
- Parameters:
backend – the qibo backend.
- Returns:
A
qibo.models.iqae.IterativeAmplitudeEstimationResultresults object.
Time evolution#
State evolution#
- class qibo.models.evolution.StateEvolution(hamiltonian, dt, solver='exp', callbacks=[], accelerators=None)[source]#
Unitary time evolution of a state vector under a Hamiltonian.
- Parameters:
hamiltonian (
qibo.hamiltonians.abstract.AbstractHamiltonian) – Hamiltonian to evolve under.dt (float) – Time step to use for the numerical integration of Schrondiger’s equation.
solver (str) – Solver to use for integrating Schrodinger’s equation. Available solvers are ‘exp’ which uses the exact unitary evolution operator and ‘rk4’ or ‘rk45’ which use Runge-Kutta methods to integrate the Schordinger’s time-dependent equation in time. When the ‘exp’ solver is used to evolve a
qibo.hamiltonians.hamiltonians.SymbolicHamiltonianthen the Trotter decomposition of the evolution operator will be calculated and used automatically. If the ‘exp’ is used on a denseqibo.core.hamiltonians.hamiltonians.Hamiltonianthe full Hamiltonian matrix will be exponentiated to obtain the exact evolution operator. Runge-Kutta solvers use simple matrix multiplications of the Hamiltonian to the state and no exponentiation is involved.callbacks (list) – List of callbacks to calculate during evolution.
accelerators (dict) – Dictionary of devices to use for distributed execution. This option is available only when the Trotter decomposition is used for the time evolution.
Example
import numpy as np from qibo import models, hamiltonians # create critical (h=1.0) TFIM Hamiltonian for three qubits hamiltonian = hamiltonians.TFIM(3, h=1.0) # initialize evolution model with step dt=1e-2 evolve = models.StateEvolution(hamiltonian, dt=1e-2) # initialize state to |+++> initial_state = np.ones(8) / np.sqrt(8) # execute evolution for total time T=2 final_state2 = evolve(final_time=2, initial_state=initial_state)
Adiabatic evolution#
- class qibo.models.evolution.AdiabaticEvolution(h0, h1, s, dt, solver='exp', callbacks=[], accelerators=None)[source]#
Adiabatic evolution of a state vector under the following Hamiltonian:
\[H(t) = (1 - s(t)) H_0 + s(t) H_1\]- Parameters:
h0 (
qibo.hamiltonians.abstract.AbstractHamiltonian) – Easy Hamiltonian.h1 (
qibo.hamiltonians.abstract.AbstractHamiltonian) – Problem Hamiltonian. These Hamiltonians should be time-independent.s (callable) – Function of time that defines the scheduling of the adiabatic evolution. Can be either a function of time s(t) or a function with two arguments s(t, p) where p corresponds to a vector of parameters to be optimized.
dt (float) – Time step to use for the numerical integration of Schrondiger’s equation.
solver (str) – Solver to use for integrating Schrodinger’s equation. Available solvers are ‘exp’ which uses the exact unitary evolution operator and ‘rk4’ or ‘rk45’ which use Runge-Kutta methods to integrate the Schordinger’s time-dependent equation in time. When the ‘exp’ solver is used to evolve a
qibo.hamiltonians.hamiltonians.SymbolicHamiltonianthen the Trotter decomposition of the evolution operator will be calculated and used automatically. If the ‘exp’ is used on a denseqibo.hamiltonians.hamiltonians.Hamiltonianthe full Hamiltonian matrix will be exponentiated to obtain the exact evolution operator. Runge-Kutta solvers use simple matrix multiplications of the Hamiltonian to the state and no exponentiation is involved.callbacks (list) – List of callbacks to calculate during evolution.
accelerators (dict) – Dictionary of devices to use for distributed execution. This option is available only when the Trotter decomposition is used for the time evolution.
- property schedule#
Returns scheduling as a function of time.
- minimize(initial_parameters, method='BFGS', options=None, messages=False)[source]#
Optimize the free parameters of the scheduling function.
- Parameters:
initial_parameters (np.ndarray) – Initial guess for the variational parameters that are optimized. The last element of the given array should correspond to the guess for the total evolution time T.
method (str) – The desired minimization method. One of
"cma"(genetic optimizer),"sgd"(gradient descent) or any of the methods supported by scipy.optimize.minimize.options (dict) – a dictionary with options for the different optimizers.
messages (bool) – If
Truethe loss evolution is shown during optimization.
Data Encoders#
We provide a family of algorithms that encode classical data into quantum circuits.
Computational Basis Encoder#
Given a bitstring \(b\) of length \(n\), this encoder generates a layer of Pauli-\(X\) gates that creates the quantum state \(|\,b\,\rangle\).
For instance, the following two circuit generations are equivalent:
b = "101"
circuit_1 = comp_basis_encoder(b)
circuit_2 = Circuit(3)
circuit_2.add(gates.X(0))
circuit_2.add(gates.X(2))
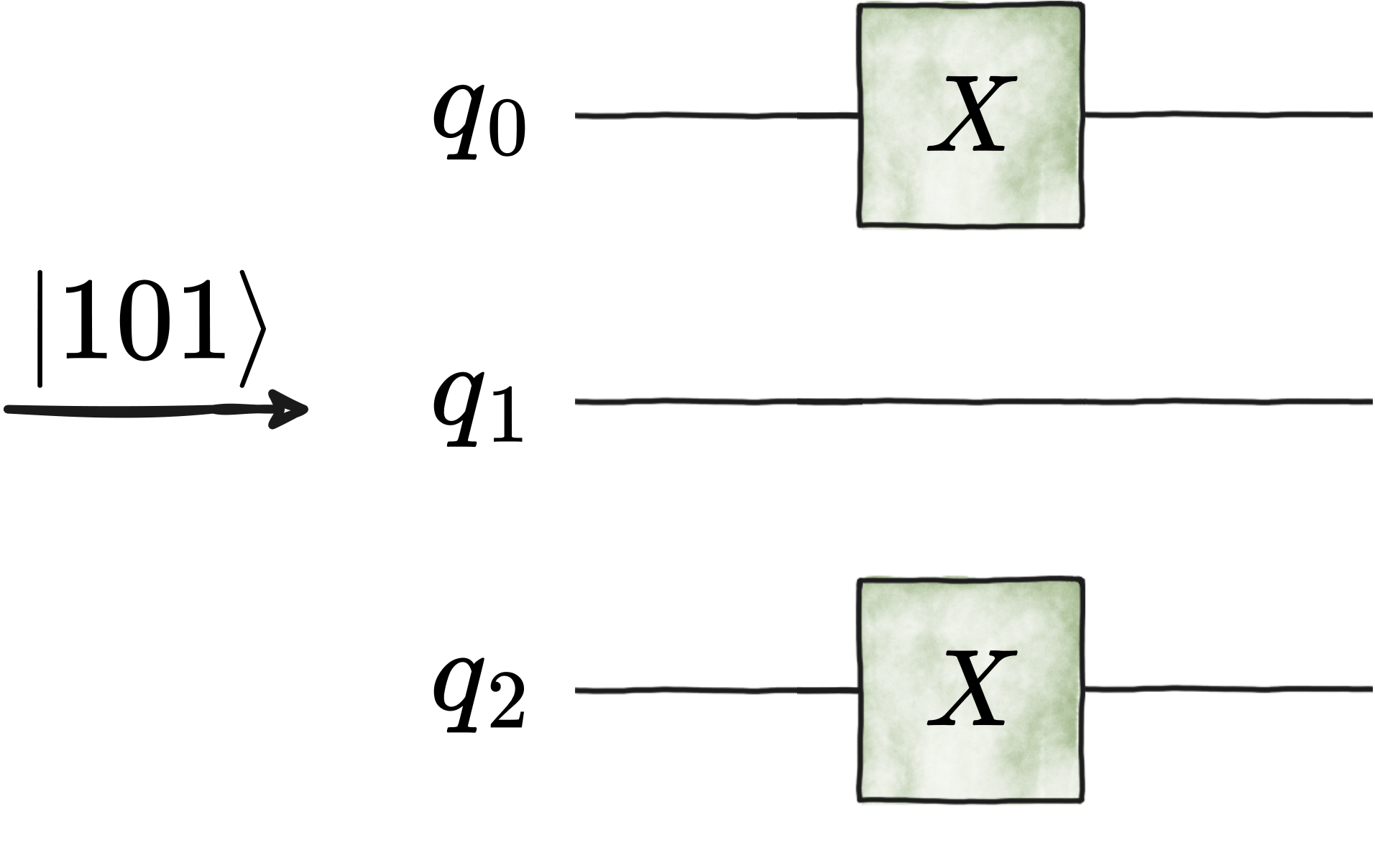
- qibo.models.encodings.comp_basis_encoder(basis_element: int | str | list | tuple, nqubits: int | None = None, **kwargs)[source]#
Create circuit that performs encoding of bitstrings into computational basis states.
- Parameters:
basis_element (int or str or list or tuple) – bitstring to be encoded. If
int,nqubitsmust be specified. Ifstr, must be composed of only \(0`s and :math:`1`s. If ``list`\) ortuple, must be composed of \(0`s and :math:`1`s as ``int`\) orstr.nqubits (int, optional) – total number of qubits in the circuit. If
basis_elementisint,nqubitsmust be specified. IfnqubitsisNone,nqubitsdefaults to length ofbasis_element. Defaults toNone.kwargs (dict, optional) – Additional arguments used to initialize a Circuit object. For details, see the documentation of
qibo.models.circuit.Circuit.
- Returns:
Circuit encoding computational basis element.
- Return type:
Phase Encoder#
Encodes data of length \(n\) into the phases of \(n\) qubits.
For instance, the following two circuit generations are equivalent:
nqubits = 3
phases = np.random.rand(nqubits)
circuit_1 = phase_encoder(phases, rotation="RX")
circuit_2 = Circuit(3)
circuit_2.add(gates.RX(qubit, phases[qubit]) for qubit in range(nqubits))
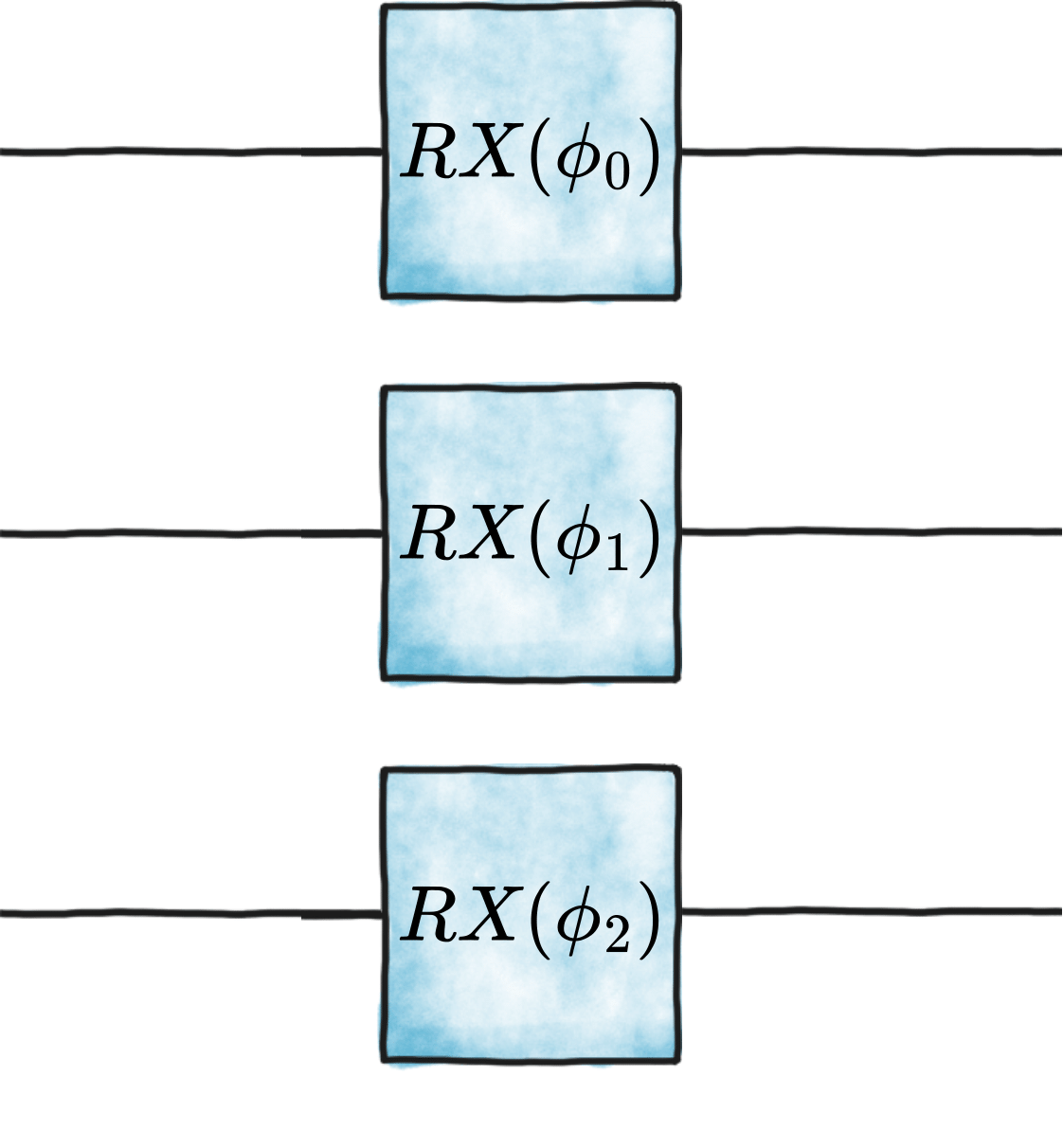
- qibo.models.encodings.phase_encoder(data, rotation: str = 'RY', backend=None, **kwargs)[source]#
Create circuit that performs the phase encoding of
data.- Parameters:
data (ndarray or list) – \(1\)-dimensional array of phases to be loaded.
rotation (str, optional) – If
"RX", usesqibo.gates.gates.RXas rotation. If"RY", usesqibo.gates.gates.RYas rotation. If"RZ", usesqibo.gates.gates.RZas rotation. Defaults to"RY".backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.kwargs (dict, optional) – Additional arguments used to initialize a Circuit object. For details, see the documentation of
qibo.models.circuit.Circuit.
- Returns:
Circuit that loads
datain phase encoding.- Return type:
Sparse encoder#
- qibo.models.encodings.sparse_encoder(data, method: str = 'li', nqubits: int = None, backend=None, **kwargs)[source]#
Create circuit that encodes \(1\)-dimensional data in a subset of amplitudes of the computational basis.
Consider a sparse-access model, where for a data vector \(\mathbf{x} \in \mathbb{C}^{d}\), with \(d = 2^{n}\) and \(s\) non-zero amplitudes, one has access to the data vector \(\mathbf{y}\) of the form
\[\mathbf{y} = \left\{ (b_{1}, x_{1}), \, \dots, \, (b_{s}, x_{s}) \right\} \, ,\]where \(\{x_{j}\}_{j\in[s]}\) is the non-zero components of \(\mathbf{x}\) and \(\{b_{j}\}_{j\in[s]}\) is the set of addresses associated with these values. Then, this function generates a quantum circuit \(s\text{-}\mathrm{Load}\) that encodes \(\mathbf{x}\) in the amplitudes of an \(n\)-qubit quantum state as
\[s\text{-}\mathrm{Load}(\mathbf{y}) \, \ket{0}^{\otimes \, n} = \sum_{j\in[s]} \, \frac{x_{j}}{\|\mathbf{x}\|_{2}} \, \ket{b_{j}} \, ,\]where \(\|\cdot\|_{2}\) is the Euclidean norm.
The resulting circuit parametrizes
datain hyperspherical coordinates in the \((2^{n} - 1)\)-unit sphere.- Parameters:
data (ndarray or list or zip) – sequence of tuples of the form \((b_{j}, x_{j})\). The addresses \(b_{j}\) can be either integers or in bitstring format of size \(n\).
method (str, optional) – method to be used, either
liorfarias. They refer to methods in references [1] and [2], respectively. Defaults tolinqubits (int, optional) – total number of qubits in the system. To be used when \(b_j\) are integers. If \(b_j\) are strings and
nqubitsisNone, defaults to the length of the strings \(b_{j}\). Defaults toNone.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.kwargs (dict, optional) – Additional arguments used to initialize a Circuit object. For details, see the documentation of
qibo.models.circuit.Circuit.
- Returns:
Circuit that loads sparse \(\mathbf{x}\).
- Return type:
References
1. L. Li, and J. Luo, Nearly Optimal Circuit Size for Sparse Quantum State Preparation arXiv:2406.16142 (2024).
2. R. M. S. Farias, T. O. Maciel, G. Camilo, R. Lin, S. Ramos-Calderer, and L. Aolita, Quantum encoder for fixed-Hamming-weight subspaces, Phys. Rev. Applied 23, 044014 (2025).
Binary encoder#
- qibo.models.encodings.binary_encoder(data, parametrization: str = 'hyperspherical', nqubits: int = None, codewords=None, keep_antictrls: bool = False, backend=None, **kwargs)[source]#
Create circuit that encodes \(1\)-dimensional data in all amplitudes of the computational basis.
Given data vector \(\mathbf{x} \in \mathbb{C}^{d}\), with \(d = 2^{n}\), this function generates a quantum circuit \(\mathrm{Load}\) that encodes \(\mathbf{x}\) in the amplitudes of an \(n\)-qubit quantum state as
\[\mathrm{Load}(\mathbf{x}) \, \ket{0}^{\otimes \, n} = \sum_{j=0}^{d-1} \, \frac{x_{j}}{\|\mathbf{x}\|_{F}} \, \ket{b_{j}} \, ,\]where \(b_{j} \in \{0, \, 1\}^{\otimes \, n}\) is the \(n\)-bit representation of the integer \(j\), \(\|\cdot\|_{F}\) is the Frobenius norm.
Resulting circuit parametrizes
datain eitherhypersphericalorhopfcoordinates in the \((2^{n} - 1)\)-unit sphere.- Parameters:
data (ndarray) – \(1\)-dimensional array or length \(d = 2^{n}\) to be loaded in the amplitudes of a \(n\)-qubit quantum state.
parametrization (str) – choice of circuit parametrization. either
hypersphericalorhopfcoordinates in the \((2^{n} - 1)\)-unit sphere.nqubits (int, optional) – total number of qubits in the system. To be used when \(b_j\) are integers. If \(b_j\) are strings and
nqubitsisNone, defaults to the length of the strings \(b_{j}\). Defaults toNone.codewords (int, optional) – list of codewords. When parametrization is
hyperspherical, the list is used to encode the data in the given order. IfNone, the codewords are set by the erhlich algorithm.keep_antictrls (bool, optional) – If
Trueand parametrization ishyperspherical, we don’t simplify the anti-controls when placing the RBS gates. For details, see [1].backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.kwargs (dict, optional) – Additional arguments used to initialize a Circuit object. For details, see the documentation of
qibo.models.circuit.Circuit.
- Returns:
Circuit that loads
datain binary encoding.- Return type:
References
1. R. M. S. Farias, T. O. Maciel, G. Camilo, R. Lin, S. Ramos-Calderer, and L. Aolita, Quantum encoder for fixed-Hamming-weight subspaces Phys. Rev. Applied 23, 044014 (2025).
3. H. S. Cohl, Fourier, Gegenbauer and Jacobi expansions for a power-law fundamental solution of the polyharmonic equation and polyspherical addition theorems, Symmetry, Integrability and Geometry: Methods and Applications 10.3842/sigma.2013.042 (2013).
Unary Encoder#
Given a classical data array \(\mathbf{x} \in \mathbb{R}^{d}\) such that
this function generate the circuit that prepares the following quantum state \(\ket{\psi} \in \mathcal{H}\):
with \(\mathcal{H} \cong \mathbb{C}^{d}\) being a \(d\)-qubit Hilbert space, and \(\|\cdot\|_{\textup{HS}}\) being the Hilbert-Schmidt norm.
Here, \(\ket{k}\) is a unary representation of the number \(k\). For instance, for \(d = 3\), the final state would be
There are multiple circuit architechtures that lead to unary encoding of classical data. For example, to encode a \(8\)-dimensional data, one could use the so-called tree architechture below:
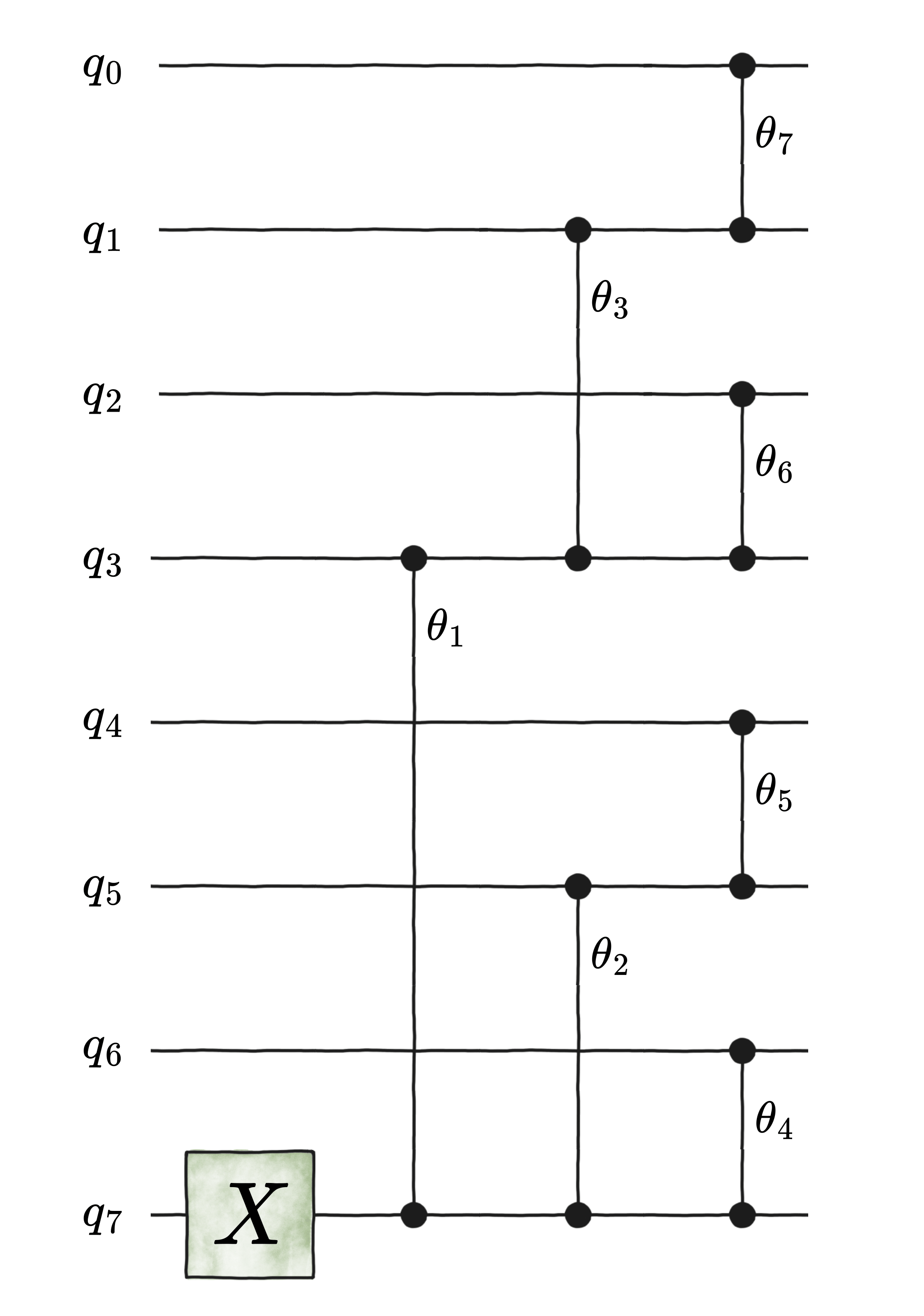
where the first gate is the qibo.gates.X
and the parametrized gates are the qibo.gates.RBS.
To know how the angles \(\{\theta_{k}\}_{[k]}\) are calculated for this architecture,
please refer to S. Johri et al., Nearest Centroid Classification on a Trapped Ion Quantum Computer,
arXiv:2012.04145v2 [quant-ph].
On the other hand, the same encoding could be performed using the so-called diagonal (also known as ladder) architecture below:
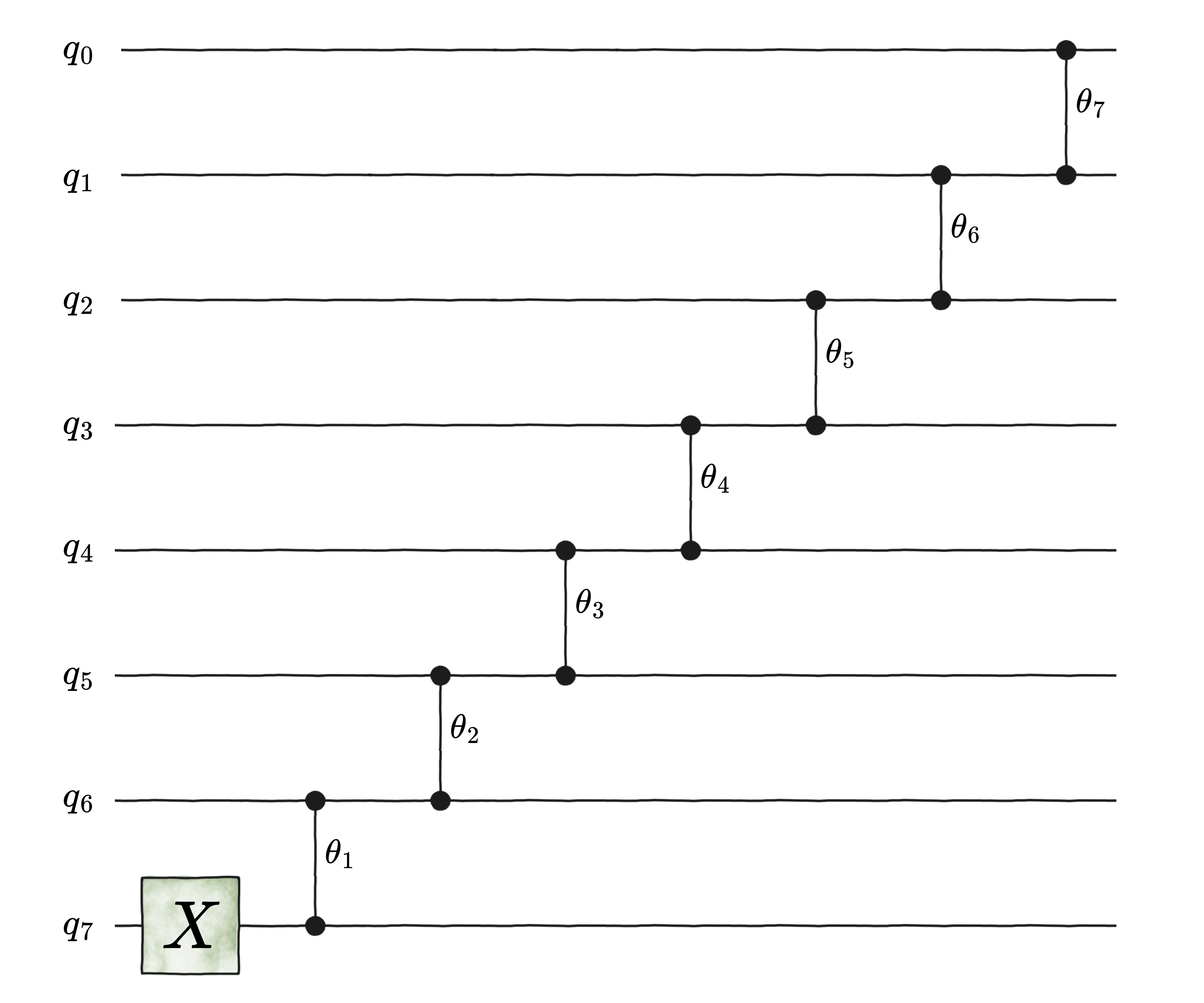
This architecture leads to a choice of angles based on spherical coordinates in a d-dimensional hypersphere.
- qibo.models.encodings.unary_encoder(data, architecture: str = 'tree', backend=None, **kwargs)[source]#
Create circuit that performs the (deterministic) unary encoding of
data.- Parameters:
data (ndarray) – \(1\)-dimensional array of data to be loaded.
architecture (str, optional) – circuit architecture used for the unary loader. If
diagonal, uses a ladder-like structure. Iftree, uses a binary-tree-based structure. Defaults totree.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.kwargs (dict, optional) – Additional arguments used to initialize a Circuit object. For details, see the documentation of
qibo.models.circuit.Circuit.
- Returns:
Circuit that loads
datain unary representation.- Return type:
Unary Encoder for Random Gaussian States#
Performs the same unary encoder as qibo.models.encodings.unary_encoder
using the tree architecture , with the difference being that now each entry
of the \(d\)-dimensional array is sampled from a Gaussian distribution
\(\mathcal{N}(0, 1)\).
- qibo.models.encodings.unary_encoder_random_gaussian(nqubits: int, architecture: str = 'tree', seed=None, backend=None, **kwargs)[source]#
Create a circuit that performs the unary encoding of a random Gaussian state.
At depth \(h\) of the tree architecture, the angles \(\theta_{k} \in [0, 2\pi]\) of the the gates \(RBS(\theta_{k})\) are sampled from the following probability density function:
\[p_{h}(\theta) = \frac{1}{2} \, \frac{\Gamma(2^{h-1})}{\Gamma^{2}(2^{h-2})} \, \left|\sin(\theta) \, \cos(\theta)\right|^{2^{h-1} - 1} \, ,\]where \(\Gamma(\cdot)\) is the Gamma function.
- Parameters:
nqubits (int) – number of qubits.
architecture (str, optional) – circuit architecture used for the unary loader. If
tree, uses a binary-tree-based structure. Defaults totree.seed (int or
numpy.random.Generator, optional) – Either a generator of random numbers or a fixed seed to initialize a generator. IfNone, initializes a generator with a random seed. Defaults toNone.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.kwargs (dict, optional) – Additional arguments used to initialize a Circuit object. For details, see the documentation of
qibo.models.circuit.Circuit.
- Returns:
Circuit that loads a random Gaussian array in unary representation.
- Return type:
References
1. A. Bouland, A. Dandapani, and A. Prakash, A quantum spectral method for simulating stochastic processes, with applications to Monte Carlo. arXiv:2303.06719v1 [quant-ph]
Fixed Hamming-weight Encoder#
- qibo.models.encodings.hamming_weight_encoder(data, nqubits: int, weight: int, full_hwp: bool = False, optimize_controls: bool = True, phase_correction: bool = True, initial_string=None, backend=None, **kwargs)[source]#
Create circuit that encodes
datain the Hamming-weight-\(k\) basis ofnqubits.Let \(\mathbf{x}\) be a \(1\)-dimensional array of size \(d = \binom{n}{k}\) and \(B_{k} \equiv \{ \ket{b_{j}} : b_{j} \in \{0, 1\}^{\otimes n} \,\, \text{and} \,\, |b_{j}| = k \}\) be a set of \(d\) computational basis states of \(n\) qubits that are represented by bitstrings of Hamming weight \(k\). Then, an amplitude encoder in the basis \(B_{k}\) is an \(n\)-qubit parameterized quantum circuit \(\operatorname{Load}_{B_{k}}\) such that
\[\operatorname{Load}(\mathbf{x}) \, \ket{0}^{\otimes n} = \frac{1}{\|\mathbf{x}\|} \, \sum_{j = 1}^{d} \, x_{j} \, \ket{b_{j}}\]- Parameters:
data (ndarray) – \(1\)-dimensional array of data to be loaded.
nqubits (int) – number of qubits.
weight (int) – Hamming weight that defines the subspace in which
datawill be encoded.full_hwp (bool, optional) – if
False, includes Pauli-\(X\) gates that prepare the first bitstring of Hamming weightk = weight. IfTrue, circuit is full Hamming weight preserving. Defaults to`False.optimize_controls (bool, optional) – if
True, removes unnecessary controlled operations. Defaults toTrue.phase_correction (bool, optional) – To be used when
datais complex-valued. IfTrue, adds a controlled-$mathrm{RZ}$ gate to the end of the circuit, adding a final phase correction. IfFalse, gate is not added. Defaults toTrue.initial_string (ndarray, optional) – Array containing the desired initial bitstring of Hamming
weight$k$. IfNone, defaults to $ket{1^{k}0^{n-k}}$. Defaults toNone.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.kwargs (dict, optional) – Additional arguments used to initialize a Circuit object. For details, see the documentation of
qibo.models.circuit.Circuit.
- Returns:
Circuit that loads
datain Hamming-weight-\(k\) representation.- Return type:
References
1. R. M. S. Farias, T. O. Maciel, G. Camilo, R. Lin, S. Ramos-Calderer, and L. Aolita, Quantum encoder for fixed-Hamming-weight subspaces Phys. Rev. Applied 23, 044014 (2025).
Entangling layer#
Generates a layer of nearest-neighbour two-qubit gates, assuming 1-dimensional connectivity.
With the exception of qibo.gates.gates.GeneralizedfSim,
any of the two-qubit gates implemented in qibo can be selected to customize the entangling layer.
If the chosen gate is parametrized, all phases are set to \(0.0\).
Note that these phases can be updated a posterior by using
qibo.models.Circuit.set_parameters().
The possible choices of layer architecture are the following, in alphabetical order:
diagonal, even_layer, next_nearest, pyramid, odd_layer, shifted, v, and x.
For instance, we show below an example of four of those architectures for nqubits = 6 and entangling_gate = "CNOT".
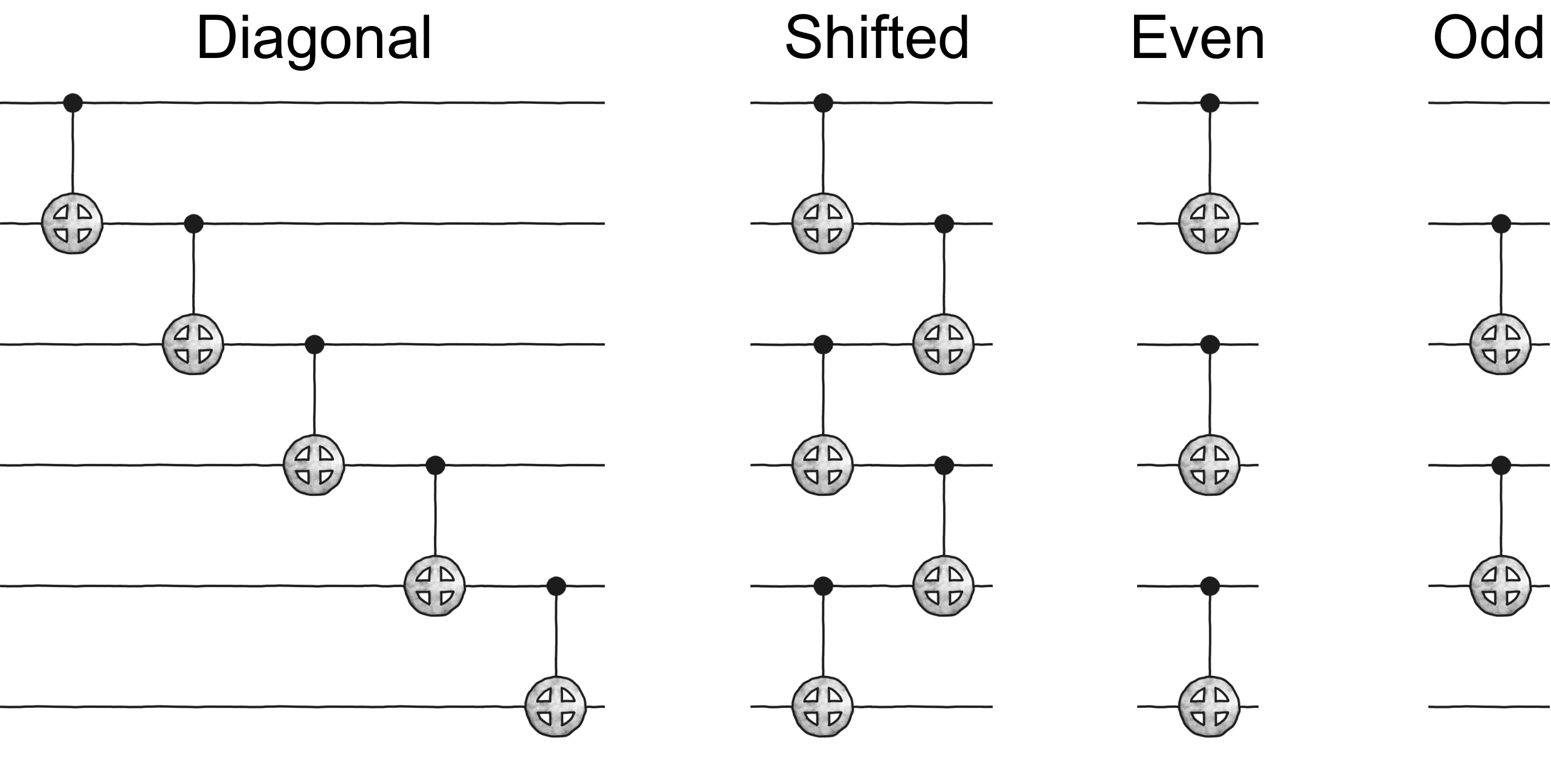
If closed_boundary is set to True, then an extra gate is added connecting the last and the first qubit,
with the last qubit as the control qubit and the first qubit as a target qubit.
- qibo.models.encodings.entangling_layer(nqubits: int, architecture: str = 'diagonal', entangling_gate: str | Gate = 'CNOT', closed_boundary: bool = False, **kwargs)[source]#
Create a layer of two-qubit entangling gates.
If the chosen gate is a parametrized gate, all phases are set to \(0.0\).
- Parameters:
nqubits (int) – Total number of qubits in the circuit.
architecture (str, optional) – Architecture of the entangling layer. In alphabetical order, options are
"diagonal","even_layer","next_nearest","odd_layer","pyramid","shifted","v", and"x". The"x"architecture is only defined for an even number of qubits. Defaults to"diagonal".entangling_gate (str or
qibo.gates.Gate, optional) – Two-qubit gate to be used in the entangling layer. Ifentangling_gateis a parametrized gate, all phases are initialized as \(0.0\). Defaults to"CNOT".closed_boundary (bool, optional) – If
Trueandarchitecture not in ["pyramid", "v", "x"], adds a closed-boundary condition to the entangling layer. Defaults toFalse.kwargs (dict, optional) – Additional arguments used to initialize a Circuit object. For details, see the documentation of
qibo.models.circuit.Circuit.
- Returns:
Circuit containing layer of two-qubit gates.
- Return type:
Greenberger-Horne-Zeilinger (GHZ) state#
- qibo.models.encodings.ghz_state(nqubits: int, **kwargs)[source]#
Generate an \(n\)-qubit Greenberger-Horne-Zeilinger (GHZ) state that takes the form
\[\ket{\text{GHZ}} = \frac{\ket{0}^{\otimes n} + \ket{1}^{\otimes n}}{\sqrt{2}}\]where \(n\) is the number of qubits.
- Parameters:
nqubits (int) – number of qubits \(n >= 2\).
kwargs (dict, optional) – additional arguments used to initialize a Circuit object. For details, see the documentation of
qibo.models.circuit.Circuit.
- Returns:
Circuit that prepares the GHZ state.
- Return type:
Dicke state#
- qibo.models.encodings.dicke_state(nqubits: int, weight: int, all_to_all: bool = False, **kwargs)[source]#
Create a circuit that prepares the Dicke state \(\ket{D_{k}^{n}}\).
The Dicke state \(\ket{D_{k}^{n}}\) is the equal superposition of all \(n\)-qubit computational basis states with fixed-Hamming-weight \(k\). The circuit prepares the state deterministically with \(O(k \, n)\) gates and \(O(n)\) depth, or \(O(k \log\frac{n}{k})\) depth under the assumption of
all-to-allconnectivity.- Parameters:
nqubits (int) – number of qubits \(n\).
weight (int) – Hamming weight \(k\) of the Dicke state.
all_to_all (bool, optional) – If
False, uses implementation from Ref. [1]. IfTrue, uses shorter-depth implementation from Ref. [2]. Defaults toFalse.kwargs (dict, optional) – additional arguments used to initialize a Circuit object. For details, see the documentation of
qibo.models.circuit.Circuit.
- Returns:
Circuit that prepares \(\ket{D_{k}^{n}}\).
- Return type:
References
1. Andreas Bärtschi and Stephan Eidenbenz, Deterministic preparation of Dicke states, 22nd International Symposium on Fundamentals of Computation Theory, FCT’19, 126-139 (2019).
2. Andreas Bärtschi and Stephan Eidenbenz, Short-Depth Circuits for Dicke State Preparation, IEEE International Conference on Quantum Computing & Engineering (QCE), 87–96 (2022).
Graph state#
- qibo.models.encodings.graph_state(matrix, backend=None, **kwargs)[source]#
Create circuit encoding an undirected graph state given its adjacency matrix.
Given a graph \(G = (V, E)\) with \(V\) being the set of vertices and \(E\) being the set of edges, an $n$-qubit graph state is defined as
\[\ket{G} = \prod_{(j, k) \in E} \, CZ_{j, k} \, \ket{+}^{\otimes V} \, ,\]where \(CZ_{a,b}\) is the
qibo.gates.CZgate acting on qubits \(j\) and \(k\), and \(\ket{+} = H \, \ket{0}$, with :class:`qibo.gates.H\) being the Hadamard gate.- Parameters:
matrix (ndarray or list) – Adjacency matrix of the graph.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.kwargs (dict, optional) – Additional arguments used to initialize a Circuit object. For details, see the documentation of
qibo.models.circuit.Circuit.
- Returns:
Circuit of the graph state with the given adjacency matrix.
- Return type:
Permutation synthesis#
- qibo.models.encodings.permutation_synthesis(sigma: List[int] | tuple[int, ...], m: int = 2, backend=None, **kwargs)[source]#
Return circuit that implements a given permutation.
Given permutation
sigmaon \(\{0, \, 1, \, \dots, \, d-1\}\) and a power‑of‑two budgetm, this function factorssigmainto the fewest layers \(\sigma_{1}, \, \sigma_{2}, \, \cdots, \, \sigma_{t}\) such that:each layer has at most \(m\) disjoint transpositions;
each layer moves a power‑of‑two number of indices.
The function returns a circuit synthesis of
sigma.- Parameters:
- Returns:
Circuit that implements the permutation
sigma.- Return type:
References
1. L. Li, and J. Luo, Nearly Optimal Circuit Size for Sparse Quantum State Preparation arXiv:2406.16142 (2024).
Error Mitigation#
Qibo allows for mitigating noise in circuits via error mitigation methods. Unlike error correction, error mitigation does not aim to correct qubit errors, but rather it provides the means to estimate the noise-free expected value of an observable measured at the end of a noisy circuit.
Readout Mitigation#
A common kind of error happening in quantum circuits is readout error, i.e. the error in the measurement of the qubits at the end of the computation. In Qibo there are currently two methods implemented for mitigating readout errors, and both can be used as standalone functions or in combination with the other general mitigation methods by setting the paramter readout.
Response Matrix#
Given \(n\) qubits, all the possible \(2^n\) states are constructed via the application of the corresponding sequence of \(X\) gates \(X_0\otimes I_1\otimes\cdot\cdot\cdot\otimes X_{n-1}\). In the presence of readout errors, we will measure for each state \(i\) some noisy frequencies \(F_i^{noisy}\) different from the ideal ones \(F_i^{ideal}=\delta_{i,j}\).
The effect of the error is modeled by the response matrix composed of the noisy frequencies as columns \(M=\big(F_0^{noisy},...,F_{n-1}^{noisy}\big)\). We have indeed that:
and, therefore, the calibration matrix obtained as \(M_{\text{cal}}=M^{-1}\) can be used to recover the noise-free frequencies.
The calibration matrix \(M_{\text{cal}}\) lacks stochasticity, resulting in a ‘negative probability’ issue. The distributions that arise after applying \(M_{\text{cal}}\) are quasiprobabilities; the individual elements can be negative surpass 1, provided they sum to 1. It is posible to use Iterative Bayesian Unfolding (IBU) to preserve non-negativity. See Nachman et al for more details.
- qibo.models.error_mitigation.get_response_matrix(nqubits, qubit_map=None, noise_model=None, nshots: int = 10000, backend=None)[source]#
Computes the response matrix for readout mitigation.
- Parameters:
nqubits (int) – Total number of qubits.
qubit_map (list, optional) – the qubit map. If None, a list of range of circuit’s qubits is used. Defaults to
None.noise_model (
qibo.noise.NoiseModel, optional) – noise model used for simulating noisy computation. This matrix can be used to mitigate the effect of qibo.noise.ReadoutError.nshots (int, optional) – number of shots. Defaults to \(10000\).
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
- the computed (nqubits, nqubits) response matrix for
readout mitigation.
- Return type:
numpy.ndarray
- qibo.models.error_mitigation.iterative_bayesian_unfolding(probabilities, response_matrix, iterations=10)[source]#
Iterative Bayesian Unfolding (IBU) method for readout mitigation.
- Parameters:
probabilities (numpy.ndarray) – the input probabilities to be unfolded.
response_matrix (numpy.ndarray) – the response matrix.
iterations (int, optional) – the number of iterations to perform. Defaults to 10.
- Returns:
the unfolded probabilities.
- Return type:
numpy.ndarray
- Reference:
B. Nachman, M. Urbanek et al, Unfolding Quantum Computer Readout Noise. arXiv:1910.01969 [quant-ph].
S. Srinivasan, B. Pokharel et al, Scalable Measurement Error Mitigation via Iterative Bayesian Unfolding. arXiv:2210.12284 [quant-ph].
- qibo.models.error_mitigation.apply_resp_mat_readout_mitigation(state, response_matrix, iterations=None)[source]#
Applies readout error mitigation to the given state using the provided response matrix.
- Parameters:
state (
qibo.measurements.CircuitResult) – the input state to be updated. This state should contain the frequencies that need to be mitigated.response_matrix (numpy.ndarray) – the response matrix for readout mitigation.
iterations (int, optional) – the number of iterations to use for the Iterative Bayesian Unfolding method. If
Nonethe ‘inverse’ method is used. Defaults toNone.
- Returns:
the input state with the updated (mitigated) frequencies.
- Return type:
qibo.measurements.CircuitResult
- qibo.models.error_mitigation.apply_randomized_readout_mitigation(circuit, noise_model=None, nshots: int = 10000, ncircuits: int = 10, qubit_map=None, seed=None, backend=None)[source]#
Readout mitigation method that transforms the bias in an expectation value into a measurable multiplicative factor.
This factor can be eliminated at the expense of increased sampling complexity for the observable.
- Parameters:
circuit (
qibo.models.Circuit) – input circuit.noise_model (
qibo.noise.NoiseModel, optional) – noise model used for simulating noisy computation. Defaults toNone.nshots (int, optional) – number of shots. Defaults to \(10000\).
ncircuits (int, optional) – number of randomized circuits. Each of them uses
int(nshots / ncircuits)shots. Defaults to 10.qubit_map (list, optional) – the qubit map. If
None, a list of range of circuit’s qubits is used. Defaults toNone.seed (int or
numpy.random.Generator, optional) – Either a generator of random numbers or a fixed seed to initialize a generator. IfNone, initializes a generator with a random seed. Default:None.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
- the state of the input circuit with
mitigated frequencies.
- Return type:
qibo.measurements.CircuitResult
References
1. Ewout van den Berg, Zlatko K. Minev et al, Model-free readout-error mitigation for quantum expectation values. arXiv:2012.09738 [quant-ph].
- qibo.models.error_mitigation.get_expectation_val_with_readout_mitigation(circuit, observable, noise_model=None, nshots: int = 10000, readout=None, qubit_map=None, seed=None, backend=None)[source]#
CDR Applies readout error mitigation to the given circuit and observable.
- Parameters:
circuit (
qibo.models.Circuit) – input circuit.observable (
qibo.hamiltonians.Hamiltonian/:class:`qibo.hamiltonians.SymbolicHamiltonian) – The observable to be measured.noise_model (qibo.models.noise.Noise, optional) – the noise model to be applied. Defaults to
None.nshots (int, optional) – the number of shots for the circuit execution. Defaults to \(10000\).
readout (dict, optional) –
a dictionary that may contain the following keys:
ncircuits: int, specifies the number of random circuits to use for the randomized method of readout error mitigation.
response_matrix: numpy.ndarray, used for applying a pre-computed response matrix for readout error mitigation.
ibu_iters: int, specifies the number of iterations for the iterative Bayesian unfolding method of readout error mitigation. If provided, the corresponding readout error mitigation method is used. Defaults to {}.
qubit_map (list, optional) – the qubit map. If None, a list of range of circuit’s qubits is used. Defaults to
None.seed (int or
numpy.random.Generator, optional) – Either a generator of random numbers or a fixed seed to initialize a generator. IfNone, initializes a generator with a random seed. Default:None.backend (qibo.backends.abstract.Backend, optional) – the backend to be used in the execution. If None, it uses the global backend. Defaults to
None.
- Returns:
the mitigated expectation value of the observable.
- Return type:
Randomized readout mitigation#
This approach converts the effect of any noise map \(A\) into a single multiplication factor for each Pauli observable, that is, diagonalizes the measurement channel. The multiplication factor \(\lambda\) can be directly measured even without the quantum circuit. Dividing the measured value \(\langle O\rangle_{noisy}\) by these factor results in the mitigated Pauli expectation value \(\langle O\rangle_{ideal}\),
This process can be implemented with the aforementioned
qibo.models.error_mitigation.apply_randomized_readout_mitigation().
Zero Noise Extrapolation (ZNE)#
Given a noisy circuit \(C\) and an observable \(A\), Zero Noise Extrapolation (ZNE) consists in running \(n+1\) versions of the circuit with different noise levels \(\{c_j\}_{j=0..n}\) and, for each of them, measuring the expected value of the observable \(E_j=\langle A\rangle_j\).
Then, an estimate for the expected value of the observable in the noise-free condition is obtained as:
with \(\gamma_j\) satisfying:
This implementation of ZNE relies on the insertion of gate pairs (that resolve to the identity in the noise-free case) to realize the different noise levels \(\{c_j\}\), see He et al for more details. Hence, the canonical levels are mapped to the number of inserted pairs as \(c_j\rightarrow 2 c_j + 1\).
- qibo.models.error_mitigation.ZNE(circuit, observable, noise_levels, noise_model=None, nshots=10000, solve_for_gammas=False, global_unitary_folding=True, insertion_gate='CNOT', readout=None, qubit_map=None, seed=None, backend=None)[source]#
Runs the Zero Noise Extrapolation method for error mitigation.
The different noise levels are realized by the insertion of pairs of either
CNOTorRX(pi/2)gates that resolve to the identiy in the noise-free case.- Parameters:
circuit (
qibo.models.Circuit) – input circuit.observable (
qibo.hamiltonians.Hamiltonian/:class:`qibo.hamiltonians.SymbolicHamiltonian) – Observable to measure.noise_levels (numpy.ndarray) – Sequence of noise levels.
noise_model (
qibo.noise.NoiseModel, optional) – Noise model applied to simulate noisy computation.nshots (int, optional) – Number of shots. Defaults to \(10000\). If None, the circuit is simulated without sampling: with statevector simulation if noise_model is not None and with density matrix simulation otherwise. Readout mitigation is not available with exact simulation.
solve_for_gammas (bool, optional) – If
True, explicitly solve the equations to obtain thegammacoefficients. Default isFalse.global_unitary_folding (bool, optional) – If
True, noise is increased by global unitary folding. IfFalse, local unitary folding is used. Defaults toTrue.insertion_gate (str, optional) – gate to be folded in the local unitary folding. If
RX, the gate used is :math:RX(\pi / 2). Otherwise, it is theCNOTgate.readout (dict, optional) –
a dictionary that may contain the following keys:
ncircuits: int, specifies the number of random circuits to use for the randomized method of readout error mitigation.
response_matrix: numpy.ndarray, used for applying a pre-computed response matrix for readout error mitigation.
ibu_iters: int, specifies the number of iterations for the iterative Bayesian unfolding method of readout error mitigation. If provided, the corresponding readout error mitigation method is used. Defaults to {}.
qubit_map (list, optional) – the qubit map. If None, a list of range of circuit’s qubits is used. Defaults to
None.seed (int or
numpy.random.Generator, optional) – Either a generator of random numbers or a fixed seed to initialize a generator. IfNone, initializes a generator with a random seed. Default:None.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Estimate of the expected value of
observablein the noise free condition.- Return type:
numpy.ndarray
- Reference:
K. Temme, S. Bravyi et al, Error mitigation for short-depth quantum circuits. arXiv:1612.02058 [quant-ph].
- qibo.models.error_mitigation.get_gammas(noise_levels, analytical: bool = True)[source]#
Standalone function to compute the ZNE coefficients given the noise levels.
- Parameters:
noise_levels (numpy.ndarray) – array containing the different noise levels. Note that in the CNOT insertion paradigm this corresponds to the number of CNOT pairs to be inserted. The canonical ZNE noise levels are obtained as
2 * c + 1.analytical (bool, optional) – if
True, computes the coeffients by solving the linear system. IfFalse, use the analytical solution valid for the CNOT insertion method. Default isTrue.
- Returns:
the computed coefficients.
- Return type:
numpy.ndarray
- qibo.models.error_mitigation.get_noisy_circuit(circuit, num_insertions: int, global_unitary_folding=True, insertion_gate=None)[source]#
Standalone function to generate the noisy circuit with the inverse gate pairs insertions.
- Parameters:
circuit (
qibo.models.circuit.Circuit) – circuit to modify.num_insertions (int) – number of insertion gate pairs / global unitary folds to add.
global_unitary_folding (bool) – If
True, noise is increased by global unitary folding. IfFalse, local unitary folding is used. Defaults toTrue.insertion_gate (str, optional) – gate to be folded in the local unitary folding. If
RX, the gate used is :math:RX(\pi / 2). Otherwise, it is theCNOTgate.
- Returns:
circuit with the inserted gate pairs or with global folding.
- Return type:
qibo.models.Circuit
Clifford Data Regression (CDR)#
In the Clifford Data Regression (CDR) method, a set of \(n\) circuits \(S_n=\{C_i\}_{i=1,..,n}\) is generated starting from the original circuit \(C_0\) by replacing some of the non-Clifford gates with Clifford ones. Given an observable \(A\), all the circuits of \(S_n\) are both simulated to obtain the correspondent expected values of \(A\) in noise-free condition \(\{a_i^{exact}\}_{i=1,..,n}\), and run in noisy conditions to obtain the noisy expected values \(\{a_i^{noisy}\}_{i=1,..,n}\).
Finally a model \(f\) is trained to minimize the mean squared error:
and learn the mapping \(a^{noisy}\rightarrow a^{exact}\). The mitigated expected value of \(A\) at the end of \(C_0\) is then obtained simply with \(f(a_0^{noisy})\).
In this implementation the initial circuit is expected to be decomposed in the three Clifford gates \(RX(\frac{\pi}{2})\), \(CNOT\), \(X\) and in \(RZ(\theta)\) (which is Clifford only for \(\theta=\frac{n\pi}{2}\)). By default the set of Clifford gates used for substitution is \(\{RZ(0),RZ(\frac{\pi}{2}),RZ(\pi),RZ(\frac{3}{2}\pi)\}\). See Sopena et al for more details.
- qibo.models.error_mitigation.CDR(circuit, observable, noise_model, nshots: int = 10000, model=<function <lambda>>, n_training_samples: int = 100, full_output: bool = False, readout=None, qubit_map=None, seed=None, backend=None)[source]#
Runs the Clifford Data Regression error mitigation method.
- Parameters:
circuit (
qibo.models.Circuit) – input circuit decomposed in the primitive gatesX,CNOT,RX(pi/2),RZ(theta).observable (
qibo.hamiltonians.Hamiltonian/:class:`qibo.hamiltonians.SymbolicHamiltonian) – observable to be measured.noise_model (
qibo.noise.NoiseModel) – noise model used for simulating noisy computation.nshots (int, optional) – Number of shots. Defaults to \(10000\). If None, the circuit is simulated without sampling: with statevector simulation if noise_model is not None and with density matrix simulation otherwise. Readout mitigation is not available with exact simulation.
model (callable, optional) – model used for fitting. This should be a callable function object
f(x, *params), taking as input the predictor variable and the parameters. Default is a simple linear modelf(x,a,b) := a*x + b.n_training_samples (int, optional) – number of training circuits to sample. Defaults to 100.
full_output (bool, optional) – if
True, this function returns additional information:val,optimal_params,train_val. Defaults toFalse.readout (dict, optional) –
a dictionary that may contain the following keys:
ncircuits: int, specifies the number of random circuits to use for the randomized method of readout error mitigation.
response_matrix: numpy.ndarray, used for applying a pre-computed response matrix for readout error mitigation.
ibu_iters: int, specifies the number of iterations for the iterative Bayesian unfolding method of readout error mitigation. If provided, the corresponding readout error mitigation method is used. Defaults to {}.
qubit_map (list, optional) – the qubit map. If None, a list of range of circuit’s qubits is used. Defaults to
None.seed (int or
numpy.random.Generator, optional) – Either a generator of random numbers or a fixed seed to initialize a generator. IfNone, initializes a generator with a random seed. Default:None.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Mitigated expectation value of observable. val (float): Noisy expectation value of observable. optimal_params (list): Optimal values for params. train_val (dict): Contains the noise-free and noisy expectation values obtained with the training circuits.
- Return type:
mit_val (float)
- Reference:
P. Czarnik, A. Arrasmith et al, Error mitigation with Clifford quantum-circuit data. arXiv:2005.10189 [quant-ph].
- qibo.models.error_mitigation.sample_training_circuit_cdr(circuit, replacement_gates: list = None, sigma: float = 0.5, seed=None, backend=None)[source]#
Samples a training circuit for CDR by susbtituting some of the non-Clifford gates.
- Parameters:
circuit (
qibo.models.Circuit) – circuit to sample from, decomposed inRX(pi/2),X,CNOTandRZgates.replacement_gates (list, optional) – candidates for the substitution of the non-Clifford gates. The
listshould be composed bytuplesof the form (gates.XYZ,kwargs). For example, phase gates are used by default:list((RZ, {'theta':0}), (RZ, {'theta':pi/2}), (RZ, {'theta':pi}), (RZ, {'theta':3*pi/2})).sigma (float, optional) – standard devation of the Gaussian distribution used for sampling.
seed (int or
numpy.random.Generator, optional) – Either a generator of random numbers or a fixed seed to initialize a generator. IfNone, initializes a generator with a random seed. Default:None.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
The sampled circuit.
- Return type:
qibo.models.Circuit
Variable Noise CDR (vnCDR)#
Variable Noise CDR (vnCDR) is an extension of the CDR method described above that factors in different noise levels as in ZNE. In detail, the set of circuits \(S_n=\{\mathbf{C}_i\}_{i=1,..,n}\) is still generated as in CDR, but for each \(\mathbf{C}_i\) we have \(k\) different versions of it with increased noise \(\mathbf{C}_i=C_i^0,C_i^1,...,C_i^{k-1}\).
Therefore, in this case we have a \(k\)-dimensional predictor variable \(\mathbf{a}_i^{noisy}=\big(a_i^0, a_i^1,..,a_i^{k-1}\big)^{noisy}\) for the same noise-free targets \(a_i^{exact}\), and we want to learn the mapping:
via minimizing the same mean squared error:
In particular, the default choice is to take \(f(\mathbf{x}):=\Gamma\cdot \mathbf{x}\;\), with \(\Gamma=\text{diag}(\gamma_0,\gamma_1,...,\gamma_{k-1})\;\), that corresponds to the ZNE calculation for the estimate of the expected value.
Here, as in the implementation of the CDR above, the circuit is supposed to be decomposed in the set of primitive gates \({RX(\frac{\pi}{2}),CNOT,X,RZ(\theta)}\). See Sopena et al for all the details.
- qibo.models.error_mitigation.vnCDR(circuit, observable, noise_levels, noise_model, nshots: int = 10000, model=None, n_training_samples: int = 100, insertion_gate: str = 'CNOT', full_output: bool = False, readout=None, qubit_map=None, seed=None, backend=None)[source]#
Runs the variable-noise Clifford Data Regression error mitigation method.
- Parameters:
circuit (
qibo.models.Circuit) – input circuit decomposed in the primitive gatesX,CNOT,RX(pi/2),RZ(theta).observable (
qibo.hamiltonians.Hamiltonian/:class:`qibo.hamiltonians.SymbolicHamiltonian) – observable to be measured.noise_levels (numpy.ndarray) – sequence of noise levels.
noise_model (
qibo.noise.NoiseModel) – noise model used for simulating noisy computation.nshots (int, optional) – Number of shots. Defaults to \(10000\). If None, the circuit is simulated without sampling: with statevector simulation if noise_model is not None and with density matrix simulation otherwise. Readout mitigation is not available with exact simulation.
model (callable, optional) – model used for fitting. This should be a callable function object
f(x, *params), taking as input the predictor variable and the parameters. Default is a simple linear modelf(x,a,b) := a*x + b.n_training_samples (int, optional) – number of training circuits to sample.
insertion_gate (str, optional) – gate to be used in the insertion. If
"RX", the gate used is :math:RX(\pi / 2). Default is"CNOT".full_output (bool, optional) – if
True, this function returns additional information:val,optimal_params,train_val. Defaults toFalse.readout (dict, optional) –
a dictionary that may contain the following keys:
ncircuits: int, specifies the number of random circuits to use for the randomized method of readout error mitigation.
response_matrix: numpy.ndarray, used for applying a pre-computed response matrix for readout error mitigation.
ibu_iters: int, specifies the number of iterations for the iterative Bayesian unfolding method of readout error mitigation. If provided, the corresponding readout error mitigation method is used. Defaults to {}.
qubit_map (list, optional) – the qubit map. If None, a list of range of circuit’s qubits is used. Defaults to
None.seed (int or
numpy.random.Generator, optional) – Either a generator of random numbers or a fixed seed to initialize a generator. IfNone, initializes a generator with a random seed. Default:None.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Mitigated expectation value of observable. val (list): Expectation value of observable with increased noise levels. optimal_params (list): Optimal values for params. train_val (dict): Contains the noise-free and noisy expectation values obtained with the training circuits.
- Return type:
mit_val (float)
- Reference:
A. Lowe, MH. Gordon et al, Unified approach to data-driven quantum error mitigation. arXiv:2011.01157 [quant-ph].
Importance Clifford Sampling (ICS)#
In the Importance Clifford Sampling (ICS) method, a set of \(n\) circuits \(S_n=\{C_i\}_{i=1,..,n}\) that stabilizes a given Pauli observable is generated starting from the original circuit \(C_0\) by replacing all the non-Clifford gates with Clifford ones. Given an observable \(A\), all the circuits of \(S_n\) are both simulated to obtain the correspondent expected values of \(A\) in noise-free condition \(\{a_i^{exact}\}_{i=1,..,n}\), and run in noisy conditions to obtain the noisy expected values \(\{a_i^{noisy}\}_{i=1,..,n}\).
Finally, a theoretically inspired model \(f\) is learned using the training data.
The mitigated expected value of \(A\) at the end of \(C_0\) is then obtained simply with \(f(a_0^{noisy})\).
In this implementation the initial circuit is expected to be decomposed in the three Clifford gates \(RX(\frac{\pi}{2})\), \(CNOT\), \(X\) and in \(RZ(\theta)\) (which is Clifford only for \(\theta=\frac{n\pi}{2}\)). By default the set of Clifford gates used for substitution is \(\{RZ(0),RZ(\frac{\pi}{2}),RZ(\pi),RZ(\frac{3}{2}\pi)\}\). See Sopena et al for more details.
- qibo.models.error_mitigation.ICS(circuit, observable, readout=None, qubit_map=None, noise_model=None, nshots=10000, n_training_samples=10, full_output=False, seed=None, backend=None)[source]#
Computes the Important Clifford Sampling method.
- Parameters:
circuit (
qibo.models.Circuit) – input circuit.observable (
qibo.hamiltonians.Hamiltonian/:class:`qibo.hamiltonians.SymbolicHamiltonian) – the observable to be measured.readout (dict, optional) –
a dictionary that may contain the following keys:
ncircuits: int, specifies the number of random circuits to use for the randomized method of readout error mitigation.
response_matrix: numpy.ndarray, used for applying a pre-computed response matrix for readout error mitigation.
ibu_iters: int, specifies the number of iterations for the iterative Bayesian unfolding method of readout error mitigation. If provided, the corresponding readout error mitigation method is used. Defaults to {}.
qubit_map (list, optional) – the qubit map. If
None, a list of range of circuit’s qubits is used. Defaults toNone.noise_model (qibo.models.noise.Noise, optional) – the noise model to be applied. Defaults to
None.nshots (int, optional) – Number of shots. Defaults to \(10000\). If None, the circuit is simulated without sampling: with statevector simulation if noise_model is not None and with density matrix simulation otherwise. Readout mitigation is not available with exact simulation.
n_training_samples (int, optional) – the number of training samples. Defaults to 10.
full_output (bool, optional) – if
True, this function returns additional information:val,optimal_params,train_val. Defaults toFalse.seed (int or
numpy.random.Generator, optional) – Either a generator of random numbers or a fixed seed to initialize a generator. IfNone, initializes a generator with a random seed. Default:None.backend (qibo.backends.abstract.Backend, optional) – the backend to be used in the execution. If None, it uses the global backend. Defaults to
None.
- Returns:
the mitigated expectated value. mitigated_expectation_std (float): the standard deviation of the mitigated expectated value. dep_param (float): the depolarizing parameter. dep_param_std (float): the standard deviation of the depolarizing parameter. lambda_list (list): the list of the depolarizing parameters. data (dict): the data dictionary containing the noise-free and noisy expectation values obtained with the training circuits.
- Return type:
mitigated_expectation (float)
- Reference:
Dayue Qin, Yanzhu Chen et al, Error statistics and scalability # pragma: no coverof quantum error mitigation formulas. arXiv:2112.06255 [quant-ph].
- qibo.models.error_mitigation.sample_clifford_training_circuit(circuit, seed=None, backend=None)[source]#
Samples a training circuit for CDR by susbtituting all the non-Clifford gates.
- Parameters:
circuit (
qibo.models.Circuit) – circuit to sample from.seed (int or
numpy.random.Generator, optional) – Either a generator of random numbers or a fixed seed to initialize a generator. IfNone, initializes a generator with a random seed. Default:None.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
the sampled circuit.
- Return type:
qibo.models.Circuit
Gates#
All supported gates can be accessed from the qibo.gates module.
Read below for a complete list of supported gates.
All gates support the controlled_by method that allows to control
the gate on an arbitrary number of qubits. For example
gates.X(0).controlled_by(1, 2)is equivalent togates.TOFFOLI(1, 2, 0),gates.RY(0, np.pi).controlled_by(1, 2, 3)applies the Y-rotation to qubit 0 when qubits 1, 2 and 3 are in the|111>state.gates.SWAP(0, 1).controlled_by(3, 4)swaps qubits 0 and 1 when qubits 3 and 4 are in the|11>state.
Abstract gate#
- class qibo.gates.abstract.Gate[source]#
The base class for gate implementation.
All base gates should inherit this class.
- draw_label#
Optional label for drawing the gate in a circuit with
qibo.models.Circuit.draw().- Type:
- is_controlled_by#
Trueif the gate was created using theqibo.gates.abstract.Gate.controlled_by()method, otherwiseFalse.- Type:
- property clifford#
Return boolean value representing if a Gate is Clifford or not.
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
- property raw: dict#
Serialize to dictionary.
The values used in the serialization should be compatible with a JSON dump (or any other one supporting a minimal set of scalar types). Though the specific implementation is up to the specific gate.
- static from_dict(raw: dict)[source]#
Load from serialization.
Essentially the counter-part of
raw().
- property qubits: Tuple[int, ...]#
Tuple with ids of all qubits (control and target) that the gate acts.
- property qasm_label: str | Tuple[str, str]#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
- property control_qubits: Tuple[int, ...]#
Tuple with ids of control qubits sorted in increasing order.
- property parameters#
Returns a tuple containing the current value of gate’s parameters.
- commutes(gate: Gate) bool[source]#
Checks if two gates commute.
- Parameters:
gate – Gate to check if it commutes with the current gate.
- Returns:
Trueif the gates commute,Falseotherwise.- Return type:
- on_qubits(qubit_map: dict) Gate[source]#
Creates the same gate targeting different qubits.
- Parameters:
qubit_map (int) – Dictionary mapping original qubit indices to new ones.
- Returns:
A
qibo.gates.Gateobject of the original gate type targeting the given qubits.
Example
from qibo import Circuit, gates circuit = Circuit(4) # Add some CNOT gates # equivalent to gates.CNOT(2, 3) circuit.add(gates.CNOT(2, 3).on_qubits({2: 2, 3: 3})) # equivalent to gates.CNOT(3, 0) circuit.add(gates.CNOT(2, 3).on_qubits({2: 3, 3: 0})) # equivalent to gates.CNOT(1, 3) circuit.add(gates.CNOT(2, 3).on_qubits({2: 1, 3: 3})) # equivalent to gates.CNOT(2, 1) circuit.add(gates.CNOT(2, 3).on_qubits({2: 2, 3: 1})) circuit.draw()
0: ───X───── 1: ───|─o─X─ 2: ─o─|─|─o─ 3: ─X─o─X───
- dagger() Gate[source]#
Returns the dagger (conjugate transpose) of the gate.
Note that dagger is not persistent for parametrized gates. For example, applying a dagger to an
qibo.gates.gates.RXgate will change the sign of its parameter at the time of application. However, if the parameter is updated after that, for example usingqibo.models.circuit.Circuit.set_parameters(), then the action of dagger will be lost.- Returns:
object representing the dagger of the original gate.
- Return type:
qibo.gates.Gate
- decompose(*free, use_toffolis: bool = True) List[Gate][source]#
Decomposes multi-control gates to gates supported by OpenQASM.
Decompositions are based on arXiv:9503016. If the gate is already controlled, it recursively decomposes the base gate and updates the control qubits accordingly.
- Parameters:
free – Ids of free qubits to use for the gate decomposition.
use_toffolis (bool, optional) – If
True, the decomposition contains onlyqibo.gates.TOFFOLIgates. IfFalse, a congruent representation is used forqibo.gates.TOFFOLIgates. Seeqibo.gates.TOFFOLIfor more details on this representation.
- Returns:
gates that have the same effect as applying the original gate.
- Return type:
- matrix(backend=None)[source]#
Returns the matrix representation of the gate.
If gate has controlled qubits inserted by
qibo.gates.Gate.controlled_by(), thenqibo.gates.Gate.matrix()returns the matrix of the original gate.from qibo import gates gate = gates.SWAP(3, 4).controlled_by(0, 1, 2) print(gate.matrix())
To return the full matrix that takes the control qubits into account, one should use
qibo.models.Circuit.unitary(), e.g.from qibo import Circuit, gates nqubits = 5 circuit = Circuit(nqubits) circuit.add(gates.SWAP(3, 4).controlled_by(0, 1, 2)) print(circuit.unitary())
- Parameters:
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.- Returns:
Matrix representation of gate.
- Return type:
ndarray
- generator_eigenvalue()[source]#
This function returns the eigenvalues of the gate’s generator.
- Returns:
eigenvalue of the generator.
- Return type:
Single qubit gates#
Hadamard (H)#
- class qibo.gates.H(q)[source]#
The Hadamard gate.
Corresponds to the following unitary matrix
\[\begin{split}\frac{1}{\sqrt{2}} \, \begin{pmatrix} 1 & 1 \\ 1 & -1 \\ \end{pmatrix}\end{split}\]- Parameters:
q (int) – the qubit id number.
- property clifford#
Return boolean value representing if a Gate is Clifford or not.
- property qasm_label#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
Pauli X (X)#
- class qibo.gates.X(q)[source]#
The Pauli-\(X\) gate.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} 0 & 1 \\ 1 & 0 \\ \end{pmatrix}\end{split}\]- Parameters:
q (int) – the qubit id number.
- property clifford#
Return boolean value representing if a Gate is Clifford or not.
- property qasm_label#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
- decompose(*free, use_toffolis: bool = True) List[Gate][source]#
Decomposes multi-control gates to gates supported by OpenQASM.
Decompositions are based on arXiv:9503016. If the gate is already controlled, it recursively decomposes the base gate and updates the control qubits accordingly.
- Parameters:
free – Ids of free qubits to use for the gate decomposition.
use_toffolis (bool, optional) – If
True, the decomposition contains onlyqibo.gates.TOFFOLIgates. IfFalse, a congruent representation is used forqibo.gates.TOFFOLIgates. Seeqibo.gates.TOFFOLIfor more details on this representation.
- Returns:
gates that have the same effect as applying the original gate.
- Return type:
Pauli Y (Y)#
- class qibo.gates.Y(q)[source]#
The Pauli-\(Y\) gate.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} 0 & -i \\ i & 0 \\ \end{pmatrix}\end{split}\]- Parameters:
q (int) – the qubit id number.
- property clifford#
Return boolean value representing if a Gate is Clifford or not.
- property qasm_label#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
Pauli Z (Z)#
- class qibo.gates.Z(q)[source]#
The Pauli-\(Z\) gate.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} 1 & 0 \\ 0 & -1 \\ \end{pmatrix}\end{split}\]- Parameters:
q (int) – the qubit id number.
- property clifford#
Return boolean value representing if a Gate is Clifford or not.
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
- property qasm_label#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
Square-root of Pauli X (SX)#
- class qibo.gates.SX(q)[source]#
The \(\sqrt{X}\) gate.
Corresponds to the following unitary matrix
\[\begin{split}\frac{1}{2} \, \begin{pmatrix} 1 + i & 1 - i \\ 1 - i & 1 + i \\ \end{pmatrix}\end{split}\]- Parameters:
q (int) – the qubit id number.
- property clifford#
Return boolean value representing if a Gate is Clifford or not.
- property qasm_label#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
S gate (S)#
- class qibo.gates.S(q)[source]#
The \(S\) gate.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} 1 & 0 \\ 0 & i \\ \end{pmatrix}\end{split}\]- Parameters:
q (int) – the qubit id number.
- property clifford#
Return boolean value representing if a Gate is Clifford or not.
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
- property qasm_label#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
T gate (T)#
- class qibo.gates.T(q)[source]#
The T gate.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} 1 & 0 \\ 0 & e^{i \pi / 4} \\ \end{pmatrix}\end{split}\]- Parameters:
q (int) – the qubit id number.
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
- property qasm_label#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
Identity (I)#
- class qibo.gates.I(*q)[source]#
The identity gate.
- Parameters:
*q (int) – the qubit id numbers.
- property clifford#
Return boolean value representing if a Gate is Clifford or not.
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
- property qasm_label#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
Align (A)#
Measurement (M)#
- class qibo.gates.M(*q, register_name: str | None = None, collapse: bool = False, basis: ~qibo.gates.abstract.Gate | str = <class 'qibo.gates.gates.Z'>, p0: ProbsType | None = None, p1: ProbsType | None = None)[source]#
The measure gate.
- Parameters:
*q (int) – id numbers of the qubits to measure. It is possible to measure multiple qubits using
gates.M(0, 1, 2, ...). If the qubits to measure are held in an iterable (eg. list) the*operator can be used, for examplegates.M(*[0, 1, 4])orgates.M(*range(5)).register_name (str, optional) – Optional name of the register to distinguish it from other registers when used in circuits.
collapse (bool) – Collapse the state vector after the measurement is performed. Can be used only for single shot measurements. If
Truethe collapsed state vector is returned. IfFalsethe measurement result is returned.basis (
qibo.gates.Gateor str or list, optional) – Basis to measure. Can be either: - a qibo gate - the string representing the gate - a callable that accepts a qubit, for example:lambda q: gates.RX(q, 0.2)- a list of the above, if a different basis will be used for each measurement qubit. Defaults is toqibo.gates.Z.p0 (dict, optional) – bitflip probability map. Can be: A dictionary that maps each measured qubit to the probability that it is flipped, a list or tuple that has the same length as the tuple of measured qubits or a single float number. If a single float is given the same probability will be used for all qubits.
p1 (dict, optional) – bitflip probability map for asymmetric bitflips. Same as
p0but controls the 1->0 bitflip probability. Ifp1isNonethenp0will be used both for 0->1 and 1->0 bitflips.
- property raw: dict#
Serialize to dictionary.
The values used in the serialization should be compatible with a JSON dump (or any other one supporting a minimal set of scalar types). Though the specific implementation is up to the specific gate.
- add(gate)[source]#
Adds target qubits to a measurement gate.
This method is only used for creating the global measurement gate used by the
qibo.models.Circuit. The user is not supposed to use this method and aValueErroris raised if he does so.- Parameters:
gate – Measurement gate to add its qubits in the current gate.
- classmethod load(payload)[source]#
Constructs a measurement gate starting from a json serialized one.
- on_qubits(qubit_map: dict) Gate[source]#
Creates the same measurement gate targeting different qubits and preserving the measurement result register.
- Parameters:
qubit_map (dict) – dictionary mapping original qubit indices to new ones.
- Returns:
object of the original gate type targeting the given qubits.
- Return type:
qibo.gates.Gate.M
Example
from qibo import Circuit, gates measurement = gates.M(0, 1) circuit = Circuit(3) circuit.add(measurement.on_qubits({0: 0, 1: 2})) assert circuit.queue[0].result is measurement.result circuit.draw()
0: ─M─ 1: ─|─ 2: ─M─
Rotation X-axis (RX)#
- class qibo.gates.RX(q, theta, trainable=True)[source]#
Rotation around the X-axis of the Bloch sphere.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} \cos \frac{\theta }{2} & -i\sin \frac{\theta }{2} \\ -i\sin \frac{\theta }{2} & \cos \frac{\theta }{2} \\ \end{pmatrix}\end{split}\]- Parameters:
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
- property qasm_label#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
Rotation Y-axis (RY)#
- class qibo.gates.RY(q, theta, trainable=True)[source]#
Rotation around the Y-axis of the Bloch sphere.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} \cos \frac{\theta }{2} & -\sin \frac{\theta }{2} \\ \sin \frac{\theta }{2} & \cos \frac{\theta }{2} \\ \end{pmatrix}\end{split}\]- Parameters:
q (int) – the qubit id number.
theta (float) – the rotation angle.
trainable (bool) – whether gate parameters can be updated using
qibo.models.circuit.Circuit.set_parameters(). Defaults toTrue.
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
- property qasm_label#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
Rotation Z-axis (RZ)#
- class qibo.gates.RZ(q, theta, trainable=True)[source]#
Rotation around the Z-axis of the Bloch sphere.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} e^{-i \theta / 2} & 0 \\ 0 & e^{i \theta / 2} \\ \end{pmatrix}\end{split}\]- Parameters:
q (int) – the qubit id number.
theta (float) – the rotation angle.
trainable (bool) – whether gate parameters can be updated using
qibo.models.circuit.Circuit.set_parameters(). Defaults toTrue.
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
- property qasm_label#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
First general unitary (U1)#
- class qibo.gates.U1(q, theta, trainable=True)[source]#
First general unitary gate.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} 1 & 0 \\ 0 & e^{i \theta} \\ \end{pmatrix}\end{split}\]- Parameters:
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
- property qasm_label#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
Second general unitary (U2)#
- class qibo.gates.U2(q, phi, lam, trainable=True)[source]#
Second general unitary gate.
Corresponds to the following unitary matrix
\[\begin{split}\frac{1}{\sqrt{2}} \begin{pmatrix} e^{-i(\phi + \lambda )/2} & -e^{-i(\phi - \lambda )/2} \\ e^{i(\phi - \lambda )/2} & e^{i (\phi + \lambda )/2} \\ \end{pmatrix}\end{split}\]- Parameters:
q (int) – the qubit id number.
phi (float) – first rotation angle.
lamb (float) – second rotation angle.
trainable (bool) – whether gate parameters can be updated using
qibo.models.circuit.Circuit.set_parameters(). Defaults toTrue.
- property qasm_label#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
Third general unitary (U3)#
- class qibo.gates.U3(q, theta, phi, lam, trainable=True)[source]#
Third general unitary gate.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} e^{-i(\phi + \lambda )/2}\cos\left (\frac{\theta }{2}\right ) & -e^{-i(\phi - \lambda )/2}\sin\left (\frac{\theta }{2}\right ) \\ e^{i(\phi - \lambda )/2}\sin\left (\frac{\theta }{2}\right ) & e^{i (\phi + \lambda )/2}\cos\left (\frac{\theta }{2}\right ) \\ \end{pmatrix}\end{split}\]- Parameters:
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
- property qasm_label#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
Two qubit gates#
Controlled-NOT (CNOT)#
- class qibo.gates.CNOT(q0, q1)[source]#
The Controlled-NOT gate.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ \end{pmatrix}\end{split}\]- property clifford#
Return boolean value representing if a Gate is Clifford or not.
- property qasm_label#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
Controlled-Y (CY)#
- class qibo.gates.CY(q0, q1)[source]#
The Controlled-\(Y\) gate.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & -i \\ 0 & 0 & i & 0 \\ \end{pmatrix}\end{split}\]- property clifford#
Return boolean value representing if a Gate is Clifford or not.
- property qasm_label#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
Controlled-phase (CZ)#
- class qibo.gates.CZ(q0, q1)[source]#
The Controlled-Phase gate.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & -1 \\ \end{pmatrix}\end{split}\]- property clifford#
Return boolean value representing if a Gate is Clifford or not.
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
- property qasm_label#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
Controlled-Square Root of X (CSX)#
- class qibo.gates.CSX(q0, q1)[source]#
The Controlled-\(\sqrt{X}\) gate.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & e^{i\pi/4} & e^{-i\pi/4} \\ 0 & 0 & e^{-i\pi/4} & e^{i\pi/4} \\ \end{pmatrix}\end{split}\]- property qasm_label#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
Controlled-rotation X-axis (CRX)#
- class qibo.gates.CRX(q0, q1, theta, trainable=True)[source]#
Controlled rotation around the X-axis for the Bloch sphere.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & \cos \frac{\theta }{2} & -i\sin \frac{\theta }{2} \\ 0 & 0 & -i\sin \frac{\theta }{2} & \cos \frac{\theta }{2} \\ \end{pmatrix}\end{split}\]- Parameters:
q0 (int) – the control qubit id number.
q1 (int) – the target qubit id number.
theta (float) – the rotation angle.
trainable (bool) – whether gate parameters can be updated using
qibo.models.circuit.Circuit.set_parameters(). Defaults toTrue.
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
- property qasm_label#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
Controlled-rotation Y-axis (CRY)#
- class qibo.gates.CRY(q0, q1, theta, trainable=True)[source]#
Controlled rotation around the Y-axis for the Bloch sphere.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & \cos \frac{\theta }{2} & -\sin \frac{\theta }{2} \\ 0 & 0 & \sin \frac{\theta }{2} & \cos \frac{\theta }{2} \\ \end{pmatrix}\end{split}\]Note that this differs from the
qibo.gates.RZgate.- Parameters:
q0 (int) – the control qubit id number.
q1 (int) – the target qubit id number.
theta (float) – the rotation angle.
trainable (bool) – whether gate parameters can be updated using
qibo.models.circuit.Circuit.set_parameters(). Defaults toTrue.
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
- property qasm_label#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
Controlled-rotation Z-axis (CRZ)#
- class qibo.gates.CRZ(q0, q1, theta, trainable=True)[source]#
Controlled rotation around the Z-axis for the Bloch sphere.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & e^{-i \theta / 2} & 0 \\ 0 & 0 & 0 & e^{i \theta / 2} \\ \end{pmatrix}\end{split}\]- Parameters:
q0 (int) – the control qubit id number.
q1 (int) – the target qubit id number.
theta (float) – the rotation angle.
trainable (bool) – whether gate parameters can be updated using
qibo.models.circuit.Circuit.set_parameters(). Defaults toTrue.
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
- property qasm_label#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
Controlled first general unitary (CU1)#
- class qibo.gates.CU1(q0, q1, theta, trainable=True)[source]#
Controlled first general unitary gate.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & e^{i \theta } \\ \end{pmatrix}\end{split}\]Note that this differs from the
qibo.gates.CRZgate.- Parameters:
q0 (int) – the control qubit id number.
q1 (int) – the target qubit id number.
theta (float) – the rotation angle.
trainable (bool) – whether gate parameters can be updated using
qibo.models.circuit.Circuit.set_parameters(). Defaults toTrue.
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
- property qasm_label#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
Controlled second general unitary (CU2)#
- class qibo.gates.CU2(q0, q1, phi, lam, trainable=True)[source]#
Controlled second general unitary gate.
Corresponds to the following unitary matrix
\[\begin{split}\frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & e^{-i(\phi + \lambda )/2} & -e^{-i(\phi - \lambda )/2} \\ 0 & 0 & e^{i(\phi - \lambda )/2} & e^{i (\phi + \lambda )/2} \\ \end{pmatrix}\end{split}\]
Controlled third general unitary (CU3)#
- class qibo.gates.CU3(q0, q1, theta, phi, lam, trainable=True)[source]#
Controlled third general unitary gate.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & e^{-i(\phi + \lambda )/2}\cos\left (\frac{\theta }{2}\right ) & -e^{-i(\phi - \lambda )/2}\sin\left (\frac{\theta }{2}\right ) \\ 0 & 0 & e^{i(\phi - \lambda )/2}\sin\left (\frac{\theta }{2}\right ) & e^{i (\phi + \lambda )/2}\cos\left (\frac{\theta }{2}\right ) \\ \end{pmatrix}\end{split}\]- Parameters:
q0 (int) – the control qubit id number.
q1 (int) – the target qubit id number.
theta (float) – first rotation angle.
phi (float) – second rotation angle.
lamb (float) – third rotation angle.
trainable (bool) – whether gate parameters can be updated using
qibo.models.circuit.Circuit.set_parameters(). Defaults toTrue.
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
- property qasm_label#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
Swap (SWAP)#
- class qibo.gates.SWAP(q0, q1)[source]#
The swap gate.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}\end{split}\]- Parameters:
- property clifford#
Return boolean value representing if a Gate is Clifford or not.
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
- property qasm_label#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
iSwap (iSWAP)#
- class qibo.gates.iSWAP(q0, q1)[source]#
The iSWAP gate.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & i & 0 \\ 0 & i & 0 & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}\end{split}\]- Parameters:
- property clifford#
Return boolean value representing if a Gate is Clifford or not.
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
- property qasm_label#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
Square root of iSwap (SiSWAP)#
- class qibo.gates.SiSWAP(q0, q1)[source]#
The \(\sqrt{\text{iSWAP}}\) gate.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1/\sqrt{2} & i/\sqrt{2} & 0 \\ 0 & i/\sqrt{2} & 1/\sqrt{2} & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}\end{split}\]- Parameters:
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
f-Swap (FSWAP)#
- class qibo.gates.FSWAP(q0, q1)[source]#
The fermionic swap gate.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & -1 \\ \end{pmatrix}\end{split}\]- Parameters:
- property clifford#
Return boolean value representing if a Gate is Clifford or not.
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
- property qasm_label#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
fSim#
- class qibo.gates.fSim(q0, q1, theta, phi, trainable=True)[source]#
The fSim gate defined in arXiv:2001.08343.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos \theta & -i\sin \theta & 0 \\ 0 & -i\sin \theta & \cos \theta & 0 \\ 0 & 0 & 0 & e^{-i \phi } \\ \end{pmatrix}\end{split}\]- Parameters:
q0 (int) – the first qubit to be swapped id number.
q1 (int) – the second qubit to be swapped id number.
theta (float) – Angle for the one-qubit rotation.
phi (float) – Angle for the
|11>phase.trainable (bool) – whether gate parameters can be updated using
qibo.models.circuit.Circuit.set_parameters(). Defaults toTrue.
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
Sycamore gate#
- class qibo.gates.SYC(q0, q1)[source]#
The Sycamore gate, defined in the Supplementary Information of Quantum supremacy using a programmable superconducting processor.
Corresponding to the following unitary matrix
\[\begin{split}\text{fSim}(\pi / 2, \, \pi / 6) = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & -i & 0 \\ 0 & -i & 0 & 0 \\ 0 & 0 & 0 & e^{-i \pi / 6} \\ \end{pmatrix} \, ,\end{split}\]where \(\text{fSim}\) is the
qibo.gates.fSimgate.- Parameters:
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
fSim with general rotation#
- class qibo.gates.GeneralizedfSim(q0, q1, unitary, phi, trainable=True)[source]#
The fSim gate with a general rotation.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & R_{00} & R_{01} & 0 \\ 0 & R_{10} & R_{11} & 0 \\ 0 & 0 & 0 & e^{-i \phi } \\ \end{pmatrix}\end{split}\]- Parameters:
q0 (int) – the first qubit to be swapped id number.
q1 (int) – the second qubit to be swapped id number.
unitary (np.ndarray) – Unitary that corresponds to the one-qubit rotation.
phi (float) – Angle for the
|11>phase.trainable (bool) – whether gate parameters can be updated using
qibo.models.circuit.Circuit.set_parameters(). Defaults toTrue.
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
- property parameters#
Returns a tuple containing the current value of gate’s parameters.
Parametric XX interaction (RXX)#
- class qibo.gates.RXX(q0, q1, theta, trainable=True)[source]#
Parametric 2-qubit XX interaction, or rotation about XX-axis.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} \cos \frac{\theta }{2} & 0 & 0 & -i\sin \frac{\theta }{2} \\ 0 & \cos \frac{\theta }{2} & -i\sin \frac{\theta }{2} & 0 \\ 0 & -i\sin \frac{\theta }{2} & \cos \frac{\theta }{2} & 0 \\ -i\sin \frac{\theta }{2} & 0 & 0 & \cos \frac{\theta }{2} \\ \end{pmatrix}\end{split}\]- Parameters:
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
- property qasm_label#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
Parametric YY interaction (RYY)#
- class qibo.gates.RYY(q0, q1, theta, trainable=True)[source]#
Parametric 2-qubit YY interaction, or rotation about YY-axis.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} \cos \frac{\theta }{2} & 0 & 0 & i\sin \frac{\theta }{2} \\ 0 & \cos \frac{\theta }{2} & -i\sin \frac{\theta }{2} & 0 \\ 0 & -i\sin \frac{\theta }{2} & \cos \frac{\theta }{2} & 0 \\ i\sin \frac{\theta }{2} & 0 & 0 & \cos \frac{\theta }{2} \\ \end{pmatrix}\end{split}\]- Parameters:
q0 (int) – the first entangled qubit id number.
q1 (int) – the second entangled qubit id number.
trainable (bool) – whether gate parameters can be updated using
qibo.models.circuit.Circuit.set_parameters(). Defaults toTrue.
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
- property qasm_label#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
Parametric ZZ interaction (RZZ)#
- class qibo.gates.RZZ(q0, q1, theta, trainable=True)[source]#
Parametric 2-qubit ZZ interaction, or rotation about ZZ-axis.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} e^{-i \theta / 2} & 0 & 0 & 0 \\ 0 & e^{i \theta / 2} & 0 & 0 \\ 0 & 0 & e^{i \theta / 2} & 0 \\ 0 & 0 & 0 & e^{-i \theta / 2} \\ \end{pmatrix}\end{split}\]- Parameters:
q0 (int) – the first entangled qubit id number.
q1 (int) – the second entangled qubit id number.
theta (float) – the rotation angle.
trainable (bool) – whether gate parameters can be updated using
qibo.models.circuit.Circuit.set_parameters(). Defaults toTrue.
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
- property qasm_label#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
Parametric ZX interaction (RZX)#
- class qibo.gates.RZX(q0, q1, theta, trainable=True)[source]#
Parametric 2-qubit ZX interaction, or rotation about ZX-axis.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} \text{RX}(\theta) & 0 \\ 0 & \text{RX}(-\theta) \\ \end{pmatrix} = \begin{pmatrix} \cos{\frac{\theta}{2}} & -i \sin{\frac{\theta}{2}} & 0 & 0 \\ -i \sin{\frac{\theta}{2}} & \cos{\frac{\theta}{2}} & 0 & 0 \\ 0 & 0 & \cos{\frac{\theta}{2}} & i \sin{\frac{\theta}{2}} \\ 0 & 0 & i \sin{\frac{\theta}{2}} & \cos{\frac{\theta}{2}} \\ \end{pmatrix} \, ,\end{split}\]where \(\text{RX}\) is the
qibo.gates.RXgate.- Parameters:
q0 (int) – the first entangled qubit id number.
q1 (int) – the second entangled qubit id number.
theta (float) – the rotation angle.
trainable (bool) – whether gate parameters can be updated using
qibo.models.circuit.Circuit.set_parameters(). Defaults toTrue.
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
Parametric XX-YY interaction (RXXYY)#
- class qibo.gates.RXXYY(q0, q1, theta, trainable=True)[source]#
Parametric 2-qubit \(XX + YY\) interaction, or rotation about \(XX + YY\)-axis.
Corresponds to the following unitary matrix
\[\begin{split}\exp\left(-i \frac{\theta}{4}(XX + YY)\right) = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos{\frac{\theta}{2}} & -i \sin{\frac{\theta}{2}} & 0 \\ 0 & -i \sin{\frac{\theta}{2}} & \cos{\frac{\theta}{2}} & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} \, ,\end{split}\]- Parameters:
q0 (int) – the first entangled qubit id number.
q1 (int) – the second entangled qubit id number.
theta (float) – the rotation angle.
trainable (bool) – whether gate parameters can be updated using
qibo.models.circuit.Circuit.set_parameters(). Defaults toTrue.
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
Givens gate#
- class qibo.gates.GIVENS(q0, q1, theta, trainable=True)[source]#
The Givens gate.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos(\theta) & -\sin(\theta) & 0 \\ 0 & \sin(\theta) & \cos(\theta) & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}\end{split}\]- Parameters:
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
Reconfigurable Beam Splitter gate (RBS)#
- class qibo.gates.RBS(q0, q1, theta, trainable=True)[source]#
The Reconfigurable Beam Splitter gate.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos(\theta) & \sin(\theta) & 0 \\ 0 & -\sin(\theta) & \cos(\theta) & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}\end{split}\]Note that, in our implementation, \(\text{RBS}(\theta) = \text{Givens}(-\theta)\), where \(\text{Givens}\) is the
qibo.gates.GIVENSgate. However, we point out that this definition is not unique.- Parameters:
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
Echo Cross-Resonance gate (ECR)#
- class qibo.gates.ECR(q0, q1)[source]#
THe Echo Cross-Resonance gate.
Corresponds ot the following matrix
\[\begin{split}\frac{1}{\sqrt{2}} \left( X \, I - Y \, X \right) = \frac{1}{\sqrt{2}} \, \begin{pmatrix} 0 & 0 & 1 & i \\ 0 & 0 & i & 1 \\ 1 & -i & 0 & 0 \\ -i & 1 & 0 & 0 \\ \end{pmatrix}\end{split}\]- property clifford#
Return boolean value representing if a Gate is Clifford or not.
Special gates#
Toffoli#
- class qibo.gates.TOFFOLI(q0, q1, q2)[source]#
The Toffoli gate.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ \end{pmatrix}\end{split}\]- Parameters:
- property qasm_label#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
- congruent(use_toffolis: bool = True) List[Gate][source]#
Congruent representation of
TOFFOLIgate.This is a helper method for the decomposition of multi-control
Xgates. The congruent representation is based on Sec. 6.2 of arXiv:9503016. The sequence of the gates produced here has the same effect asTOFFOLIwith the phase of the|101>state reversed.- Parameters:
use_toffolis – If
Truea singleTOFFOLIgate is returned. IfFalsethe congruent representation is returned.- Returns:
List with
RYandCNOTgates that have the same effect as applying the originalTOFFOLIgate.
CCZ#
- class qibo.gates.CCZ(q0, q1, q2)[source]#
The controlled-CZ gate.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 \\ \end{pmatrix}\end{split}\]- Parameters:
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
- property qasm_label#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
Deutsch#
- class qibo.gates.DEUTSCH(q0, q1, q2, theta, trainable=True)[source]#
The Deutsch gate.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & i \cos{\theta} & \sin{\theta} \\ 0 & 0 & 0 & 0 & 0 & 0 & \sin{\theta} & i \cos{\theta} \\ \end{pmatrix}\end{split}\]- Parameters:
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
Fan-out#
- class qibo.gates.FanOut(*q)[source]#
The \(\textrm{FanOut}\) gate.
Given a register containing \(k \geq 2\) qubits, this gate is equivalent to \(k - 1\)
qibo.gates.CNOTgates in which the control qubit for all CNOTs is the first qubit in the register while the each CNOT has each of the remaining qubits in the register as its target qubit.- Parameters:
*q (int) – Ids of the qubits which the gate acts on. The first id is considered to be the control qubit.
- property clifford#
Return boolean value representing if a Gate is Clifford or not.
Generalized Reconfigurable Beam Splitter (RBS)#
- class qibo.gates.GeneralizedRBS(qubits_in: Tuple[int] | List[int], qubits_out: Tuple[int] | List[int], theta: float, phi: float = 0.0, trainable: bool = True)[source]#
The generalized (complex) Reconfigurable Beam Splitter gate (\(\text{gRBS}\)).
Given a register called
qubits_incontaining \(m\) qubits and a register namedqubits_outcontaining \(m'\) qubits, the \(\text{gRBS}\) is a \((m + m')\)-qubit gate that has the following matrix representation:\[\begin{split}\begin{pmatrix} I & & & & \\ & e^{-i\phi}\cos\theta & & e^{-i\phi}\sin\theta & \\ & & I' & & \\ & -e^{i\phi}\sin\theta & & e^{i\phi}\cos\theta & \\ & & & & I\\ \end{pmatrix} \,\, ,\end{split}\]where \(I\) and \(I'\) are, respectively, identity matrices of size \(2^{m} - 1\) and \(2^{m}(2^{m'} - 2)\).
This unitary matrix is also known as a Givens rotation.
References
1. R. M. S. Farias, T. O. Maciel, G. Camilo, R. Lin, S. Ramos-Calderer, and L. Aolita, Quantum encoder for fixed-Hamming-weight subspaces, Phys. Rev. Applied 23, 044014 (2025)
- Parameters:
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
Arbitrary unitary#
- class qibo.gates.Unitary(unitary, *q, trainable=True, name: str = None, check_unitary: bool = True)[source]#
Arbitrary unitary gate.
- Parameters:
unitary – Unitary matrix as a tensor supported by the backend.
*q (int) – Qubit id numbers that the gate acts on.
trainable (bool) – whether gate parameters can be updated using
qibo.models.circuit.Circuit.set_parameters(). Defaults toTrue.name (str) – Optional name for the gate.
check_unitary (bool) – if
True, checks ifunitaryis an unitary operator. IfFalse, check is not performed andunitaryattribute defaults toFalse. Note that, even when the check is performed, there is no enforcement. This allows the user to create non-unitary gates. Default isTrue.
- property parameters#
Returns a tuple containing the current value of gate’s parameters.
- property clifford#
Return boolean value representing if a Gate is Clifford or not.
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
- on_qubits(qubit_map: dict)[source]#
Creates the same gate targeting different qubits.
- Parameters:
qubit_map (int) – Dictionary mapping original qubit indices to new ones.
- Returns:
A
qibo.gates.Gateobject of the original gate type targeting the given qubits.
Example
from qibo import Circuit, gates circuit = Circuit(4) # Add some CNOT gates # equivalent to gates.CNOT(2, 3) circuit.add(gates.CNOT(2, 3).on_qubits({2: 2, 3: 3})) # equivalent to gates.CNOT(3, 0) circuit.add(gates.CNOT(2, 3).on_qubits({2: 3, 3: 0})) # equivalent to gates.CNOT(1, 3) circuit.add(gates.CNOT(2, 3).on_qubits({2: 1, 3: 3})) # equivalent to gates.CNOT(2, 1) circuit.add(gates.CNOT(2, 3).on_qubits({2: 2, 3: 1})) circuit.draw()
0: ───X───── 1: ───|─o─X─ 2: ─o─|─|─o─ 3: ─X─o─X───
Callback gate#
- class qibo.gates.CallbackGate(callback: Callback)[source]#
Calculates a
qibo.callbacks.Callbackat a specific point in the circuit.This gate performs the callback calulation without affecting the state vector.
- Parameters:
callback (
qibo.callbacks.Callback) – Callback object to calculate.
Fusion gate#
- class qibo.gates.FusedGate(*q)[source]#
Collection of gates that will be fused and applied as single gate during simulation. This gate is constructed automatically by
qibo.models.circuit.Circuit.fuse()and should not be used by user.- matrix(backend=None)[source]#
Returns matrix representation of special gate.
- Parameters:
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.- Returns:
Matrix representation of special gate.
- Return type:
ndarray
IONQ Native gates#
GPI#
- class qibo.gates.GPI(q, phi, trainable=True)[source]#
The GPI gate.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} 0 & e^{- i \phi} \\ e^{i \phi} & 0 \\ \end{pmatrix}\end{split}\]- Parameters:
- property qasm_label#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
GPI2#
- class qibo.gates.GPI2(q, phi, trainable=True)[source]#
The GPI2 gate.
Corresponds to the following unitary matrix
\[\begin{split}\frac{1}{\sqrt{2}} \, \begin{pmatrix} 1 & -i e^{- i \phi} \\ -i e^{i \phi} & 1 \\ \end{pmatrix}\end{split}\]- Parameters:
- property qasm_label#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
- property clifford#
Return boolean value representing if a Gate is Clifford or not.
Mølmer–Sørensen (MS)#
- class qibo.gates.MS(q0, q1, phi0, phi1, theta: float = 1.5707963267948966, trainable=True)[source]#
The Mølmer–Sørensen (MS) gate is a two-qubit gate native to trapped ions.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} \cos(\theta / 2) & 0 & 0 & -i e^{-i( \phi_0 + \phi_1)} \sin(\theta / 2) \\ 0 & \cos(\theta / 2) & -i e^{-i( \phi_0 - \phi_1)} \sin(\theta / 2) & 0 \\ 0 & -i e^{i( \phi_0 - \phi_1)} \sin(\theta / 2) & \cos(\theta / 2) & 0 \\ -i e^{i( \phi_0 + \phi_1)} \sin(\theta / 2) & 0 & 0 & \cos(\theta / 2) \\ \end{pmatrix}\end{split}\]- Parameters:
q0 (int) – the first qubit to be swapped id number.
q1 (int) – the second qubit to be swapped id number.
phi0 (float) – first qubit’s phase.
phi1 (float) – second qubit’s phase
theta (float, optional) – arbitrary angle in the interval \(0 \leq \theta \leq \pi /2\). If \(\theta \rightarrow \pi / 2\), the fully-entangling MS gate is defined. Defaults to \(\pi / 2\).
trainable (bool) – whether gate parameters can be updated using
qibo.models.circuit.Circuit.set_parameters(). Defaults toTrue.
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
- property qasm_label#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
Quantinuum native gates#
U1q#
- class qibo.gates.U1q(q, theta, phi, trainable=True)[source]#
Native single-qubit gate in the Quantinuum platform.
Corresponds to the following unitary matrix:
\[\begin{split}\begin{pmatrix} \cos\left(\frac{\theta}{2}\right) & -i \, e^{-i \, \phi} \, \sin\left(\frac{\theta}{2}\right) \\ -i \, e^{i \, \phi} \, \sin\left(\frac{\theta}{2}\right) & \cos\left(\frac{\theta}{2}\right) \\ \end{pmatrix}\end{split}\]Note that \(U_{1q}(\theta, \phi) = U_{3}(\theta, \phi - \frac{\pi}{2}, \frac{\pi}{2} - \phi)\), where \(U_{3}\) is
qibo.gates.U3.- Parameters:
q (int) – the qubit id number.
theta (float) – first rotation angle.
phi (float) – second rotation angle.
trainable (bool) – whether gate parameters can be updated using
qibo.models.circuit.Circuit.set_parameters(). Defaults toTrue.
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
Note
The other Quantinuum single-qubit and two-qubit native gates are implemented in Qibo as:
Pauli-\(Z\) rotation:
qibo.gates.RZArbitrary \(ZZ\) rotation:
qibo.gates.RZZFully-entangling \(ZZ\)-interaction: \(R_{ZZ}(\pi/2)\)
IQM native gates#
Phase-\(RX\)#
- class qibo.gates.PRX(q, theta, phi, trainable=True)[source]#
Phase \(RX\) gate.
Corresponds to the following unitary matrix
\[\begin{split}\begin{pmatrix} \cos{(\theta / 2)} & -i e^{-i \phi} \sin{(\theta / 2)} \\ -i e^{i \phi} \sin{(\theta / 2)} & \cos{(\theta / 2)} \end{pmatrix}\end{split}\]- Parameters:
q (int) – the qubit id number.
theta (float) – the first angle corresponding to a rotation angle.
phi (float) – the second angle correspoding to a phase angle.
trainable (bool) – whether gate parameters can be updated using
qibo.models.circuit.Circuit.set_parameters(). Defaults toTrue.
- property hamming_weight#
Return boolean value representing if a Gate is Hamming-weight-preserving or not.
- property qasm_label#
String corresponding to OpenQASM operation of the gate. For more exotic gates, both the internal qibo name of the gate and the custom gate QASM definition are returned as a tuple for broader compatibility.
Note
The other IQM two-qubit native gate is implemented in Qibo as:
Controlled-\(Z\) rotation:
qibo.gates.CZ
Channels#
Channels are implemented in Qibo as additional gates and can be accessed from
the qibo.gates module. Channels can be used on density matrices to perform
noisy simulations. Channels that inherit qibo.gates.UnitaryChannel
can also be applied to state vectors using sampling and repeated execution.
For more information on the use of channels to simulate noise we refer to
How to perform noisy simulation?
The following channels are currently implemented:
Kraus channel#
- class qibo.gates.KrausChannel(qubits, operators)[source]#
General channel defined by arbitrary Kraus operators.
Implements the following transformation:
\[\mathcal{E}(\rho ) = \sum _k A_k \rho A_k^\dagger\]where A are arbitrary Kraus operators given by the user. Note that Kraus operators set should be trace preserving, however this is not checked. Simulation of this gate requires the use of density matrices. For more information on channels and Kraus operators please check J. Preskill’s notes.
- Parameters:
qubits (int or list or tuple) – Qubits that the Kraus operators act on. Type
intandtuplewill be considered as the same qubit ids for all operators. Alistshould contain tuples of qubits corresponding to each operator. Can be[]ifoperatorsare of typeqibo.gates.Gate, otherwise adds given gates on specified qubits.operators (list) – List of Kraus operators
Akas matrices of typendarray | tf.Tensoror gatesqibo.gates.Gate.
Example
import numpy as np from qibo import Circuit, gates # initialize circuit with 3 qubits circuit = Circuit(3, density_matrix=True) # define a sqrt(0.4) * X gate a_1 = np.sqrt(0.4) * np.array([[0, 1], [1, 0]]) # define a sqrt(0.6) * CNOT gate a_2 = np.sqrt(0.6) * np.array([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 0, 1], [0, 0, 1, 0]]) # define the channel rho -> 0.4 X{1} rho X{1} + 0.6 CNOT{0, 2} rho CNOT{0, 2} channel_1 = gates.KrausChannel([(1,), (0, 2)], [a_1, a_2]) # add channel to the circuit circuit.add(channel_1) # define the same channel using qibo.gates.Unitary a_1 = gates.Unitary(a_1, 1) a_2 = gates.Unitary(a_2, 0, 2) channel_2 = gates.KrausChannel([], [a_1, a_2]) # add channel to the circuit circuit.add(channel_2) # define the channel rho -> 0.4 X{0} rho X{0} + 0.6 CNOT{1, 2} rho CNOT{1, 2} channel_3 = gates.KrausChannel([(0,), (1, 2)], [a_1, a_2]) # add channel to the circuit circuit.add(channel_3)
- on_qubits(qubit_map: dict)[source]#
Creates the same gate targeting different qubits.
- Parameters:
qubit_map (int) – Dictionary mapping original qubit indices to new ones.
- Returns:
A
qibo.gates.Gateobject of the original gate type targeting the given qubits.
Example
from qibo import Circuit, gates circuit = Circuit(4) # Add some CNOT gates # equivalent to gates.CNOT(2, 3) circuit.add(gates.CNOT(2, 3).on_qubits({2: 2, 3: 3})) # equivalent to gates.CNOT(3, 0) circuit.add(gates.CNOT(2, 3).on_qubits({2: 3, 3: 0})) # equivalent to gates.CNOT(1, 3) circuit.add(gates.CNOT(2, 3).on_qubits({2: 1, 3: 3})) # equivalent to gates.CNOT(2, 1) circuit.add(gates.CNOT(2, 3).on_qubits({2: 2, 3: 1})) circuit.draw()
0: ───X───── 1: ───|─o─X─ 2: ─o─|─|─o─ 3: ─X─o─X───
Unitary channel#
- class qibo.gates.UnitaryChannel(qubits, operators)[source]#
Channel that is a probabilistic sum of unitary operations.
Implements the following transformation:
\[\mathcal{E}(\rho ) = \left (1 - \sum _k p_k \right )\rho + \sum _k p_k U_k \rho U_k^\dagger\]where U are arbitrary unitary operators and p are floats between 0 and 1. Note that unlike
qibo.gates.KrausChannelwhich requires density matrices, it is possible to simulate the unitary channel using state vectors and probabilistic sampling. For more information on this approach we refer to Using repeated execution.- Parameters:
qubits (int or list or tuple) – Qubits that the unitary operators act on. Types
intandtuplewill be considered as the same qubit(s) for all unitaries. Alistshould contain tuples of qubits corresponding to each operator. Can be[]ifoperatorsare of typeqibo.gates.Gate, otherwise adds given gates on specified qubits.operators (list) – List of operators as pairs
(pk, Uk)wherepkis float probability corresponding to a unitaryUkof typendarray/tf.Tensoror gatesqibo.gates.Gate.
- on_qubits(qubit_map: dict)[source]#
Creates the same gate targeting different qubits.
- Parameters:
qubit_map (int) – Dictionary mapping original qubit indices to new ones.
- Returns:
A
qibo.gates.Gateobject of the original gate type targeting the given qubits.
Example
from qibo import Circuit, gates circuit = Circuit(4) # Add some CNOT gates # equivalent to gates.CNOT(2, 3) circuit.add(gates.CNOT(2, 3).on_qubits({2: 2, 3: 3})) # equivalent to gates.CNOT(3, 0) circuit.add(gates.CNOT(2, 3).on_qubits({2: 3, 3: 0})) # equivalent to gates.CNOT(1, 3) circuit.add(gates.CNOT(2, 3).on_qubits({2: 1, 3: 3})) # equivalent to gates.CNOT(2, 1) circuit.add(gates.CNOT(2, 3).on_qubits({2: 2, 3: 1})) circuit.draw()
0: ───X───── 1: ───|─o─X─ 2: ─o─|─|─o─ 3: ─X─o─X───
Pauli noise channel#
- class qibo.gates.PauliNoiseChannel(qubits: Tuple[int, list, tuple], operators: list)[source]#
Multi-qubit noise channel that applies Pauli operators with given probabilities.
Implements the following transformation:
\[\mathcal{E}(\rho ) = \left (1 - \sum _{k} p_{k} \right ) \, \rho + \sum_{k} \, p_{k} \, P_{k} \, \rho \, P_{k}\]where \(P_{k}\) is the \(k\)-th Pauli
stringand \(p_{k}\) is the probability associated to \(P_{k}\).Example
from itertools import product import numpy as np from qibo.gates.channels import PauliNoiseChannel qubits = (0, 2) nqubits = len(qubits) # excluding the Identity operator paulis = list(product(["I", "X"], repeat=nqubits))[1:] # this next line is optional paulis = [''.join(pauli) for pauli in paulis] probabilities = np.random.rand(len(paulis) + 1) probabilities /= np.sum(probabilities) #Excluding probability of Identity operator probabilities = probabilities[1:] channel = PauliNoiseChannel( qubits, list(zip(paulis, probabilities)) )
This channel can be simulated using either density matrices or state vectors and sampling with repeated execution. See How to perform noisy simulation? for more information.
- Parameters:
- on_qubits(qubit_map: dict)[source]#
Creates the same gate targeting different qubits.
- Parameters:
qubit_map (int) – Dictionary mapping original qubit indices to new ones.
- Returns:
A
qibo.gates.Gateobject of the original gate type targeting the given qubits.
Example
from qibo import Circuit, gates circuit = Circuit(4) # Add some CNOT gates # equivalent to gates.CNOT(2, 3) circuit.add(gates.CNOT(2, 3).on_qubits({2: 2, 3: 3})) # equivalent to gates.CNOT(3, 0) circuit.add(gates.CNOT(2, 3).on_qubits({2: 3, 3: 0})) # equivalent to gates.CNOT(1, 3) circuit.add(gates.CNOT(2, 3).on_qubits({2: 1, 3: 3})) # equivalent to gates.CNOT(2, 1) circuit.add(gates.CNOT(2, 3).on_qubits({2: 2, 3: 1})) circuit.draw()
0: ───X───── 1: ───|─o─X─ 2: ─o─|─|─o─ 3: ─X─o─X───
Depolarizing channel#
- class qibo.gates.DepolarizingChannel(qubits, lam: float)[source]#
\(n\)-qubit Depolarizing quantum error channel,
\[\mathcal{E}(\rho ) = (1 - \lambda) \rho + \lambda \text{Tr}_q[\rho]\otimes \frac{I}{2^n}\]where \(\lambda\) is the depolarizing error parameter and \(0 \le \lambda \le 4^n / (4^n - 1)\).
If \(\lambda = 1\) this is a completely depolarizing channel \(E(\rho) = I / 2^n\)
If \(\lambda = 4^n / (4^n - 1)\) this is a uniform Pauli error channel: \(E(\rho) = \sum_j P_j \rho P_j / (4^n - 1)\) for all \(P_j \neq I\).
- Parameters:
- on_qubits(qubit_map: dict)[source]#
Creates the same gate targeting different qubits.
- Parameters:
qubit_map (int) – Dictionary mapping original qubit indices to new ones.
- Returns:
A
qibo.gates.Gateobject of the original gate type targeting the given qubits.
Example
from qibo import Circuit, gates circuit = Circuit(4) # Add some CNOT gates # equivalent to gates.CNOT(2, 3) circuit.add(gates.CNOT(2, 3).on_qubits({2: 2, 3: 3})) # equivalent to gates.CNOT(3, 0) circuit.add(gates.CNOT(2, 3).on_qubits({2: 3, 3: 0})) # equivalent to gates.CNOT(1, 3) circuit.add(gates.CNOT(2, 3).on_qubits({2: 1, 3: 3})) # equivalent to gates.CNOT(2, 1) circuit.add(gates.CNOT(2, 3).on_qubits({2: 2, 3: 1})) circuit.draw()
0: ───X───── 1: ───|─o─X─ 2: ─o─|─|─o─ 3: ─X─o─X───
Thermal relaxation channel#
- class qibo.gates.ThermalRelaxationChannel(qubit: int, parameters: list)[source]#
Single-qubit thermal relaxation error channel.
Implements the following transformation:
If \(T_1 \geq T_2\):
\[\mathcal{E} (\rho ) = (1 - p_z - p_0 - p_1) \rho + p_z \, Z\rho Z + \mathrm{Tr}_{q}[\rho] \otimes (p_0 | 0\rangle \langle 0| + p_1|1\rangle \langle 1|)\]while if \(T_1 < T_2\):
\[\mathcal{E}(\rho ) = \mathrm{Tr}_\mathcal{X} \left[\Lambda_{\mathcal{X}\mathcal{Y}} (\rho_\mathcal{X}^T \otimes I_{\mathcal{Y}}) \right]\]with
\[\begin{split}\Lambda = \begin{pmatrix} 1 - p_1 & 0 & 0 & e^{-t / T_2} \\ 0 & p_1 & 0 & 0 \\ 0 & 0 & p_0 & 0 \\ e^{-t / T_2} & 0 & 0 & 1 - p_0 \end{pmatrix}\end{split}\]where \(p_0 = (1 - e^{-t / T_1})(1 - \eta )\), \(p_1 = (1 - e^{-t / T_1})\eta\), and \(p_z = (e^{-t / T_1} - e^{-t / T_2})/2\). Here \(\eta\) is the
excited_populationand \(t\) is thetime, both controlled by the user. This gate is based on Qiskit’s thermal relaxation error channel.- Parameters:
qubit (int) – Qubit id that the noise channel acts on.
parameters (list) – list of 3 or 4 parameters (t_1, t_2, time, excited_population=0), where t_1 (float): T1 relaxation time. Should satisfy
t_1 > 0. t_2 (float): T2 dephasing time. Should satisfyt_1 > 0andt_2 < 2 * t_1. time (float): the gate time for relaxation error. excited_population (float): the population of the excited state at equilibrium. Default is 0.
- on_qubits(qubit_map: dict)[source]#
Creates the same gate targeting different qubits.
- Parameters:
qubit_map (int) – Dictionary mapping original qubit indices to new ones.
- Returns:
A
qibo.gates.Gateobject of the original gate type targeting the given qubits.
Example
from qibo import Circuit, gates circuit = Circuit(4) # Add some CNOT gates # equivalent to gates.CNOT(2, 3) circuit.add(gates.CNOT(2, 3).on_qubits({2: 2, 3: 3})) # equivalent to gates.CNOT(3, 0) circuit.add(gates.CNOT(2, 3).on_qubits({2: 3, 3: 0})) # equivalent to gates.CNOT(1, 3) circuit.add(gates.CNOT(2, 3).on_qubits({2: 1, 3: 3})) # equivalent to gates.CNOT(2, 1) circuit.add(gates.CNOT(2, 3).on_qubits({2: 2, 3: 1})) circuit.draw()
0: ───X───── 1: ───|─o─X─ 2: ─o─|─|─o─ 3: ─X─o─X───
Amplitude damping channel#
- class qibo.gates.AmplitudeDampingChannel(qubit, gamma: float)[source]#
Single-qubit amplitude damping channel in its Kraus representation, i.e.
\[\begin{split}K_{0} = \begin{pmatrix} 1 & 0 \\ 0 & \sqrt{1 - \gamma} \\ \end{pmatrix} \,\, , \,\, K_{1} = \begin{pmatrix} 0 & \sqrt{\gamma} \\ 0 & 0 \\ \end{pmatrix}\end{split}\]- Parameters:
- on_qubits(qubit_map: dict)[source]#
Creates the same gate targeting different qubits.
- Parameters:
qubit_map (int) – Dictionary mapping original qubit indices to new ones.
- Returns:
A
qibo.gates.Gateobject of the original gate type targeting the given qubits.
Example
from qibo import Circuit, gates circuit = Circuit(4) # Add some CNOT gates # equivalent to gates.CNOT(2, 3) circuit.add(gates.CNOT(2, 3).on_qubits({2: 2, 3: 3})) # equivalent to gates.CNOT(3, 0) circuit.add(gates.CNOT(2, 3).on_qubits({2: 3, 3: 0})) # equivalent to gates.CNOT(1, 3) circuit.add(gates.CNOT(2, 3).on_qubits({2: 1, 3: 3})) # equivalent to gates.CNOT(2, 1) circuit.add(gates.CNOT(2, 3).on_qubits({2: 2, 3: 1})) circuit.draw()
0: ───X───── 1: ───|─o─X─ 2: ─o─|─|─o─ 3: ─X─o─X───
Phase damping channel#
- class qibo.gates.PhaseDampingChannel(qubit, gamma: float)[source]#
Single-qubit phase damping channel in its Kraus representation, i.e.
\[\begin{split}K_{0} = \begin{pmatrix} 1 & 0 \\ 0 & \sqrt{1 - \gamma} \\ \end{pmatrix} \,\, , \,\, K_{1} = \begin{pmatrix} 0 & 0 \\ 0 & \sqrt{\gamma} \\ \end{pmatrix}\end{split}\]- Parameters:
- on_qubits(qubit_map)[source]#
Creates the same gate targeting different qubits.
- Parameters:
qubit_map (int) – Dictionary mapping original qubit indices to new ones.
- Returns:
A
qibo.gates.Gateobject of the original gate type targeting the given qubits.
Example
from qibo import Circuit, gates circuit = Circuit(4) # Add some CNOT gates # equivalent to gates.CNOT(2, 3) circuit.add(gates.CNOT(2, 3).on_qubits({2: 2, 3: 3})) # equivalent to gates.CNOT(3, 0) circuit.add(gates.CNOT(2, 3).on_qubits({2: 3, 3: 0})) # equivalent to gates.CNOT(1, 3) circuit.add(gates.CNOT(2, 3).on_qubits({2: 1, 3: 3})) # equivalent to gates.CNOT(2, 1) circuit.add(gates.CNOT(2, 3).on_qubits({2: 2, 3: 1})) circuit.draw()
0: ───X───── 1: ───|─o─X─ 2: ─o─|─|─o─ 3: ─X─o─X───
Readout error channel#
- class qibo.gates.ReadoutErrorChannel(qubits: Tuple[int, list, tuple], probabilities)[source]#
Readout error channel implemented as a quantum-to-classical channel.
- Parameters:
Example
For 1 qubit, the transition matrix \(P\) would be
\[\begin{split}P = \begin{pmatrix} p(0 \, | \, 0) & p(1 \, | \, 0) \\ p(0 \, | \, 1) & p(1 \, | \, 1) \end{pmatrix} \, .\end{split}\]- on_qubits(qubit_map: dict)[source]#
Creates the same gate targeting different qubits.
- Parameters:
qubit_map (int) – Dictionary mapping original qubit indices to new ones.
- Returns:
A
qibo.gates.Gateobject of the original gate type targeting the given qubits.
Example
from qibo import Circuit, gates circuit = Circuit(4) # Add some CNOT gates # equivalent to gates.CNOT(2, 3) circuit.add(gates.CNOT(2, 3).on_qubits({2: 2, 3: 3})) # equivalent to gates.CNOT(3, 0) circuit.add(gates.CNOT(2, 3).on_qubits({2: 3, 3: 0})) # equivalent to gates.CNOT(1, 3) circuit.add(gates.CNOT(2, 3).on_qubits({2: 1, 3: 3})) # equivalent to gates.CNOT(2, 1) circuit.add(gates.CNOT(2, 3).on_qubits({2: 2, 3: 1})) circuit.draw()
0: ───X───── 1: ───|─o─X─ 2: ─o─|─|─o─ 3: ─X─o─X───
Reset channel#
- class qibo.gates.ResetChannel(qubit, probabilities)[source]#
Single-qubit reset channel.
Implements the following transformation:
\[\mathcal{E}(\rho ) = (1 - p_{0} - p_{1}) \rho + \mathrm{Tr}_{q}[\rho] \otimes (p_{0} \, |0\rangle \langle 0| + p_{1} \, |1\rangle \langle 1|),\]- Parameters:
- on_qubits(qubit_map: dict)[source]#
Creates the same gate targeting different qubits.
- Parameters:
qubit_map (int) – Dictionary mapping original qubit indices to new ones.
- Returns:
A
qibo.gates.Gateobject of the original gate type targeting the given qubits.
Example
from qibo import Circuit, gates circuit = Circuit(4) # Add some CNOT gates # equivalent to gates.CNOT(2, 3) circuit.add(gates.CNOT(2, 3).on_qubits({2: 2, 3: 3})) # equivalent to gates.CNOT(3, 0) circuit.add(gates.CNOT(2, 3).on_qubits({2: 3, 3: 0})) # equivalent to gates.CNOT(1, 3) circuit.add(gates.CNOT(2, 3).on_qubits({2: 1, 3: 3})) # equivalent to gates.CNOT(2, 1) circuit.add(gates.CNOT(2, 3).on_qubits({2: 2, 3: 1})) circuit.draw()
0: ───X───── 1: ───|─o─X─ 2: ─o─|─|─o─ 3: ─X─o─X───
Noise#
In Qibo it is possible to create a custom noise model using the
class qibo.noise.NoiseModel. This enables the user to create
circuits where the noise is gate and qubit dependent.
For more information on the use of qibo.noise.NoiseModel see
How to perform noisy simulation?
- class qibo.noise.NoiseModel[source]#
Class for the implementation of a custom noise model.
Example:
from qibo import Circuit, gates from qibo.noise import NoiseModel, PauliError # Build specific noise model with 2 quantum errors: # - Pauli error on H only for qubit 1. # - Pauli error on CNOT for all the qubits. noise_model = NoiseModel() noise_model.add(PauliError([("X", 0.5)]), gates.H, 1) noise_model.add(PauliError([("Y", 0.5)]), gates.CNOT) # Generate noiseless circuit. circuit = Circuit(2) circuit.add([gates.H(0), gates.H(1), gates.CNOT(0, 1)]) # Apply noise to the circuit according to the noise model. noisy_circuit = noise_model.apply(circuit)
- add(error, gate: Gate | None = None, qubits: int | tuple | None = None, conditions=None)[source]#
Add a quantum error for a specific gate and qubit to the noise model.
- Parameters:
error – quantum error to associate with the gate. Possible choices are
qibo.noise.PauliError,qibo.noise.DepolarizingError,qibo.noise.ThermalRelaxationError,qibo.noise.AmplitudeDampingError,qibo.noise.PhaseDampingError,qibo.noise.ReadoutError,qibo.noise.ResetError,qibo.noise.UnitaryError,qibo.noise.KrausError, andqibo.noise.CustomError.gate (
qibo.gates.Gate, optional) – gate after which the noise will be added. IfNone, the noise will be added after each gate exceptqibo.gates.Channelandqibo.gates.M.qubits (int or tuple, optional) – qubits where the noise will be applied. If
None, the noise will be added after every instance of the gate. Defaults toNone.condition (callable, optional) – function that takes
qibo.gates.Gateobject as an input and returnsTrueif noise should be added to it.
Example:
import numpy as np from qibo import Circuit, gates from qibo.noise import NoiseModel, PauliError # Check if a gate is RX(pi/2). def is_sqrt_x(gate): return np.pi/2 in gate.parameters # Build a noise model with a Pauli error on RX(pi/2) gates. error = PauliError(list(zip(["X", "Y", "Z"], [0.01, 0.5, 0.1]))) noise = NoiseModel() noise.add(PauliError([("X", 0.5)]), gates.RX, conditions=is_sqrt_x) # Generate a noiseless circuit. circuit = Circuit(1) circuit.add(gates.RX(0, np.pi / 2)) circuit.add(gates.RX(0, 3 * np.pi / 2)) circuit.add(gates.X(0)) # Apply noise to the circuit. noisy_circuit = noise.apply(circuit)
- apply(circuit)[source]#
Generate a noisy quantum circuit according to the noise model built.
- Parameters:
circuit (
qibo.models.circuit.Circuit) – quantum circuit- Returns:
- initial circuit with noise gates
added according to the noise model.
- Return type:
Quantum errors#
The quantum errors available to build a noise model are the following:
- class qibo.noise.KrausError(ops)[source]#
Quantum error associated with the
qibo.gates.KrausChannel.- Parameters:
ops (list) – List of Kraus operators of type
np.ndarrayortf.Tensorand of the same shape.
- class qibo.noise.UnitaryError(probabilities, unitaries)[source]#
Quantum error associated with the
qibo.gates.UnitaryChannel.- Parameters:
- class qibo.noise.PauliError(operators)[source]#
Quantum error associated with the
qibo.gates.PauliNoiseChannel.- Parameters:
operators (list) – see
qibo.gates.PauliNoiseChannel
- class qibo.noise.DepolarizingError(lam)[source]#
Quantum error associated with the
qibo.gates.DepolarizingChannel.- Parameters:
options (float) – see
qibo.gates.DepolarizingChannel
- class qibo.noise.ThermalRelaxationError(t1, t2, time, excited_population=0)[source]#
Quantum error associated with the
qibo.gates.ThermalRelaxationChannel.- Parameters:
options (tuple) – see
qibo.gates.ThermalRelaxationChannel
- class qibo.noise.AmplitudeDampingError(gamma)[source]#
Quantum error associated with the
qibo.gates.AmplitudeDampingChannel.- Parameters:
options (float) – see
qibo.gates.AmplitudeDampingChannel
- class qibo.noise.PhaseDampingError(gamma)[source]#
Quantum error associated with the
qibo.gates.PhaseDampingChannel.- Parameters:
options (float) – see
qibo.gates.PhaseDampingChannel
- class qibo.noise.ReadoutError(probabilities)[source]#
Quantum error associated with :class:’qibo.gates;ReadoutErrorChannel’.
- Parameters:
options (array) – see :class:’qibo.gates.ReadoutErrorChannel’
- class qibo.noise.ResetError(p0, p1)[source]#
Quantum error associated with the qibo.gates.ResetChannel.
- Parameters:
options (tuple) – see
qibo.gates.ResetChannel
- class qibo.noise.CustomError(channel)[source]#
Quantum error associated with the
qibo.gates.Channel- Parameters:
channel (
qibo.gates.Channel) – any channel
Example:
import numpy as np from qibo.gates import KrausChannel from qibo.noise import CustomError # define |0><0| a1 = np.array([[1, 0], [0, 0]]) # define |0><1| a2 = np.array([[0, 1], [0, 0]]) # Create an Error associated with Kraus Channel # rho -> |0><0| rho |0><0| + |0><1| rho |0><1| error = CustomError(gates.KrausChannel((0,), [a1, a2]))
IBMQ noise model#
In Qibo, it is possible to build noisy circuits based on IBMQ’s reported noise model of
for its quantum computer by using the qibo.noise.IBMQNoiseModel class.
The noise model is built using a combination of the
qibo.gates.ThermalRelaxationChannel and qibo.gates.DepolarizingChannel
channels. . At the end of the circuit, if the qubit is measured,
bitflips errors are set. Moreover, the model handles idle qubits by applying a thermal
relaxation channel for the duration of the idle-time.
For more information on the qibo.noise.IBMQNoiseModel class, see the
example on Simulating quantum hardware.
- class qibo.noise.IBMQNoiseModel[source]#
Class for the implementation of a IBMQ noise model.
This noise model applies a
qibo.gates.DepolarizingChannelfollowed by aqibo.gates.ThermalRelaxationChannelafter each one- or two-qubit gate in the circuit. It also applies single-qubitqibo.gates.ReadoutErrorChannelbefore every measurement gate.Example:
from qibo import Circuit, gates from qibo.models.encodings import phase_encoder from qibo.noise import DepolarizingError, ThermalRelaxationError, ReadoutError from qibo.noise import IBMQNoiseModel, NoiseModel nqubits = 4 # creating circuit phases = list(range(nqubits)) circuit = phase_encoder(phases, rotation="RY") circuit.add(gates.CNOT(qubit, qubit + 1) for qubit in range(nqubits - 1)) circuit.add(gates.M(qubit) for qubit in range(1, nqubits - 1)) # creating noise model from dictionary parameters = { "depolarizing_one_qubit" : {"0": 0.1, "2": 0.04, "3": 0.15}, "depolarizing_two_qubit": {"0-1": 0.2}, "t1" : {"0": 0.1, "1": 0.2, "3": 0.01}, "t2" : {"0": 0.01, "1": 0.02, "3": 0.0001}, "gate_times" : (0.1, 0.2), "excited_population" : 0.1, "readout_one_qubit" : {"0": (0.1, 0.1), "1": 0.1, "3": [0.1, 0.1]}, } noise_model = IBMQNoiseModel() noise_model.from_dict(parameters) noisy_circuit = noise_model.apply(circuit)
- from_dict(parameters: dict)[source]#
Method used to pass noise
parametersas inside dictionary.- Parameters:
parameters (dict) –
Contains parameters necessary to initialise
qibo.noise.DepolarizingError,qibo.noise.ThermalRelaxationError, andqibo.noise.ReadoutError.The keys and values of the dictionary parameters are defined below:
"depolarizing_one_qubit"(int or float or dict): Ifintorfloat, all qubits share the same single-qubit depolarizing parameter. Ifdict, expects qubit indexes as keys and their respective depolarizing parameter as values. Seeqibo.gates.channels.DepolarizingChannelfor a detailed definition of depolarizing parameter.
"depolarizing_two_qubit"(int or float or dict): Ifintorfloat, all two-qubit gates share the same two-qubit depolarizing parameter regardless in which pair of qubits the two-qubit gate is acting on. Ifdict, expects pair qubit indexes as keys separated by a hiphen (e.g. “0-1” for gate that has “0” as control and “1” as target) and their respective depolarizing parameter as values. Seeqibo.gates.channels.DepolarizingChannelfor a detailed definition of depolarizing parameter.
"t1"(int or float or dict): Ifintorfloat, all qubitsshare the same
t1. Ifdict, expects qubit indexes as keys and its respectivet1as values. Seeqibo.gates.channels.ThermalRelaxationChannelfor a detailed definition oft1. Note thatt1andt2must be passed with the same type.
"t2"(int or float or dict): Ifintorfloat, all qubits sharethe same
t2. Ifdict, expects qubit indexes as keys and its respectivet2as values. Seeqibo.gates.channels.ThermalRelaxationChannelfor a detailed definition oft2. Note thatt2andt1must be passed with the same type.
"gate_times"(tuple or list): pair of gate times representinggate times for
ThermalRelaxationErrorfollowing, respectively, one- and two-qubit gates.
"excited_population"(int or float): SeeThermalRelaxationChannel.
"readout_one_qubit"(int or float or dict): Ifintorfloat,\(p(0|1) = p(1|0)\), and all qubits share the same readout error probabilities. If
dict, expects qubit indexes as keys and values astuple(orlist) in the format \((p(0|1),\,p(1|0))\). If values aretupleorlistof length 1 orfloatorint, then it is assumed that \(p(0|1) = p(1|0)\).
Hamiltonians#
The main abstract Hamiltonian object of Qibo is:
- class qibo.hamiltonians.abstract.AbstractHamiltonian[source]#
Qibo abstraction for Hamiltonian objects.
- abstract property matrix#
Return the full matrix representation.
For \(n\) qubits, can be a dense \(2^{n} \times 2^{n}\) array or a sparse matrix, depending on how the Hamiltonian was created.
- abstract eigenvalues(k=6)[source]#
Computes the eigenvalues for the Hamiltonian.
- Parameters:
k (int) – Number of eigenvalues to calculate if the Hamiltonian was created using a sparse matrix. This argument is ignored if the Hamiltonian was created using a dense matrix. See
qibo.backends.abstract.AbstractBackend.eigvalsh()for more details.
- abstract eigenvectors(k=6)[source]#
Computes a tensor with the eigenvectors for the Hamiltonian.
- Parameters:
k (int) – Number of eigenvalues to calculate if the Hamiltonian was created using a sparse matrix. This argument is ignored if the Hamiltonian was created using a dense matrix. See
qibo.backends.abstract.AbstractBackend.eigh()for more details.
- ground_state()[source]#
Computes the ground state of the Hamiltonian.
Uses
qibo.hamiltonians.AbstractHamiltonian.eigenvectors()and returns eigenvector corresponding to the lowest energy.
- abstract exp(a)[source]#
Computes a tensor corresponding to \(\exp(-i \, a \, H)\).
- Parameters:
a (complex) – Complex number to multiply Hamiltonian before exponentiation.
- abstract expectation(circuit, nshots: int | None = None)[source]#
Computes the expectation value for a given circuit.
- Parameters:
circuit (Circuit) – circuit to calculate the expectation value from. If the circuit has already been executed, this will just make use of the cached result, otherwise it will execute the circuit.
nshots (int, optional) – number of shots to calculate the expectation value, if
Noneit will try to compute the exact expectation value (if possible). Defaults toNone.
- Returns:
The expectation value.
- Return type:
Matrix Hamiltonian#
The first implementation of Hamiltonians uses the full matrix representation of the Hamiltonian operator in the computational basis. For \(n\) qubits, this matrix has size \(2^{n} \times 2^{n}\). Therefore, its construction is feasible only when \(n\) is small.
Alternatively, the user can construct this Hamiltonian using a sparse matrices.
Sparse matrices from the
scipy.sparse
module are supported by the numpy and qibojit backends while the
tensorflow.sparse can be
used for tensorflow. Scipy sparse matrices support algebraic
operations (addition, subtraction, scalar multiplication), linear algebra
operations (eigenvalues, eigenvectors, matrix exponentiation) and
multiplication to dense or other sparse matrices. All these properties are
inherited by qibo.hamiltonians.Hamiltonian objects created
using sparse matrices. Tensorflow sparse matrices support only multiplication
to dense matrices. Both backends support calculating Hamiltonian expectation
values using a sparse Hamiltonian matrix.
- class qibo.hamiltonians.Hamiltonian(nqubits, matrix, backend=None)[source]#
Hamiltonian based on a dense or sparse matrix representation.
- Parameters:
nqubits (int) – number of quantum bits.
matrix (ndarray) – Matrix representation of the Hamiltonian in the computational basis as an array of shape \(2^{n} \times 2^{n}\). Sparse matrices based on
scipy.sparsefornumpy/qibojitbackends (or ontf.sparsefor thetensorflowbackend) are also supported.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- property matrix#
Returns the full matrix representation.
For \(n\) qubits, can be a dense \(2^{n} \times 2^{n}\) array or a sparse matrix, depending on how the Hamiltonian was created.
- eigenvalues(k=6)[source]#
Computes the eigenvalues for the Hamiltonian.
- Parameters:
k (int) – Number of eigenvalues to calculate if the Hamiltonian was created using a sparse matrix. This argument is ignored if the Hamiltonian was created using a dense matrix. See
qibo.backends.abstract.AbstractBackend.eigvalsh()for more details.
- eigenvectors(k=6)[source]#
Computes a tensor with the eigenvectors for the Hamiltonian.
- Parameters:
k (int) – Number of eigenvalues to calculate if the Hamiltonian was created using a sparse matrix. This argument is ignored if the Hamiltonian was created using a dense matrix. See
qibo.backends.abstract.AbstractBackend.eigh()for more details.
- exp(a)[source]#
Computes a tensor corresponding to \(\exp(-i \, a \, H)\).
- Parameters:
a (complex) – Complex number to multiply Hamiltonian before exponentiation.
- expectation(circuit, nshots=None, qubit_map=None)[source]#
Computes the expectation value for a given circuit. This works only for diagonal observables if
nshots != None.- Parameters:
circuit (
qibo.models.circuit.Circuit) – circuit to calculate the expectation value from. If the circuit has already been executed, this will just make use of the cached result, otherwise it will execute the circuit.nshots (int, optional) – number of shots to calculate the expectation value, if
Noneit will try to compute the exact expectation value (if possible). Defaults toNone.
- Returns:
The expectation value.
- Return type:
- expectation_from_samples(frequencies: Dict[str | int, int], qubit_map: Tuple[int, ...] | None = None)[source]#
Compute the expectation value starting from some samples, works only for diagonal observables.
- energy_fluctuation(circuit)[source]#
Evaluate energy fluctuation:
\[\Xi_{k}(\mu) = \sqrt{\bra{\mu} \, H^{2} \, \ket{\mu} - \bra{\mu} \, H \, \ket{\mu}^2} \, .\]for a given state \(\ket{\mu}\).
- Parameters:
circuit (
qibo.models.circuit.Circuit) – circuit to compute the energy fluctuation from.- Returns:
Energy fluctuation value.
- Return type:
Symbolic Hamiltonian#
Qibo allows the user to define Hamiltonians using sympy symbols. In this
case the full Hamiltonian matrix is not constructed unless this is required.
This makes the implementation more efficient for larger qubit numbers.
For more information on constructing Hamiltonians using symbols we refer to the
How to define custom Hamiltonians using symbols? example.
- class qibo.hamiltonians.SymbolicHamiltonian(form: Expr, nqubits: int | None = None, backend: Backend | None = None)[source]#
Hamiltonian based on a symbolic representation.
Calculations using symbolic Hamiltonians are either done directly using the given
sympyexpression as it is (form) or by parsing the correspondingterms(which areqibo.core.terms.SymbolicTermobjects). The latter approach is more computationally costly as it uses asympy.expandcall on the given form before parsing the terms. For this reason thetermsare calculated only when needed, for example during Trotterization. The dense matrix of the symbolic Hamiltonian can be calculated directly fromformwithout requiringtermscalculation (seeqibo.core.hamiltonians.SymbolicHamiltonian.calculate_dense()for details).- Parameters:
form (sympy.Expr) – Hamiltonian form as a
sympy.Expr. Ideally the Hamiltonian should be written using Qibo symbols. See How to define custom Hamiltonians using symbols? example for more details.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- property dense: MatrixHamiltonian#
Creates the equivalent Hamiltonian matrix.
- property terms#
List of terms of which the Hamiltonian is a sum of.
Terms will be objects of type
qibo.core.terms.HamiltonianTerm.
- property simple_terms: Tuple[List[float], List[str], List[Tuple[int, ...]]]#
A simpler (more framework agnostic) representation of the of terms composing the Hamiltonian, defined as: their scalar coefficients, the strings of the names of their observables and the qubits they act on
- Returns:
(Tuple[List[float], List[str], List[Tuple[int, …]]])
- property diagonal_terms: list[list[qibo.hamiltonians.terms.SymbolicTerm]]#
List of terms that can be diagonalized simultaneously, i.e. that commute with each other. In detail each element of the list is a sublist of commuting ``SymbolicTerm``s.
- property diagonal_simple_terms: Tuple[List[List[float]], List[List[str]], List[List[Tuple[int, ...]]]]#
A simpler (more framework agnostic) representation of the simultaneously diagonalizable terms of the hamiltonian, defined as: their scalar coefficients, the strings of the names of their observables and the qubits they act on.
- Returns:
Tuple[List[List[float]], List[List[str]], List[List[Tuple[int, …]]]]
- property matrix#
Returns the full matrix representation.
Consisting of \(2^{n} \times 2^{n}`\) elements.
- eigenvalues(k=6)[source]#
Computes the eigenvalues for the Hamiltonian.
- Parameters:
k (int) – Number of eigenvalues to calculate if the Hamiltonian was created using a sparse matrix. This argument is ignored if the Hamiltonian was created using a dense matrix. See
qibo.backends.abstract.AbstractBackend.eigvalsh()for more details.
- eigenvectors(k=6)[source]#
Computes a tensor with the eigenvectors for the Hamiltonian.
- Parameters:
k (int) – Number of eigenvalues to calculate if the Hamiltonian was created using a sparse matrix. This argument is ignored if the Hamiltonian was created using a dense matrix. See
qibo.backends.abstract.AbstractBackend.eigh()for more details.
- ground_state()[source]#
Computes the ground state of the Hamiltonian.
Uses
qibo.hamiltonians.AbstractHamiltonian.eigenvectors()and returns eigenvector corresponding to the lowest energy.
- exp(a)[source]#
Computes a tensor corresponding to \(\exp(-i \, a \, H)\).
- Parameters:
a (complex) – Complex number to multiply Hamiltonian before exponentiation.
- expectation(circuit: Circuit, nshots: int | None = None) float[source]#
Computes the expectation value for a given circuit.
- Parameters:
circuit (
qibo.models.circuit.Circuit) – circuit to calculate the expectation value from. If the circuit has already been executed, this will just make use of the cached result, otherwise it will execute the circuit.nshots (int, optional) – number of shots to calculate the expectation value, if
Noneit will try to compute the exact expectation value (if possible). Defaults toNone.
- Returns:
The expectation value.
- Return type:
- expectation_from_samples(frequencies: Dict[str | int, int], qubit_map: Tuple[int, ...] | None = None)[source]#
Compute the expectation value starting from some samples, works only for diagonal observables.
When a qibo.hamiltonians.SymbolicHamiltonian is used for time
evolution then Qibo will automatically perform this evolution using the Trotter
of the evolution operator. This is done by automatically splitting the Hamiltonian
to sums of commuting terms, following the description of Sec. 4.1 of
arXiv:1901.05824.
For more information on time evolution we refer to the
How to simulate time evolution? example.
In addition to the abstract Hamiltonian models, Qibo provides the following pre-coded Hamiltonians:
Non-interacting Pauli-X#
- class qibo.hamiltonians.X(nqubits, dense: bool = True, backend=None)[source]#
Non-interacting Pauli-\(X\) Hamiltonian.
\[H = - \sum _{k=0}^N \, X_{k} \, .\]- Parameters:
nqubits (int) – number of qubits.
dense (bool, optional) – If
Trueit creates the Hamiltonian as aqibo.core.hamiltonians.Hamiltonian, otherwise it creates aqibo.core.hamiltonians.SymbolicHamiltonian. Defaults toTrue.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
Non-interacting Pauli-Y#
- class qibo.hamiltonians.Y(nqubits, dense: bool = True, backend=None)[source]#
Non-interacting Pauli-\(Y\) Hamiltonian.
\[H = - \sum _{k=0}^{N} \, Y_{k} \, .\]- Parameters:
nqubits (int) – number of qubits.
dense (bool) – If
Trueit creates the Hamiltonian as aqibo.core.hamiltonians.Hamiltonian, otherwise it creates aqibo.core.hamiltonians.SymbolicHamiltonian.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
Non-interacting Pauli-Z#
- class qibo.hamiltonians.Z(nqubits, dense: bool = True, backend=None)[source]#
Non-interacting Pauli-\(Z\) Hamiltonian.
\[H = - \sum _{k=0}^{N} \, Z_{k} \, .\]- Parameters:
nqubits (int) – number of qubits.
dense (bool) – If
Trueit creates the Hamiltonian as aqibo.core.hamiltonians.Hamiltonian, otherwise it creates aqibo.core.hamiltonians.SymbolicHamiltonian.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
Transverse field Ising model#
Max Cut#
- class qibo.hamiltonians.MaxCut(nqubits, dense: bool = True, adj_matrix: list[list[float]] | ndarray | None = None, backend: Backend | None = None)[source]#
Max Cut Hamiltonian.
\[H = -\frac{1}{2} \, \sum _{j, k = 0}^{N} \, \left(1 - Z_{j} \, Z_{k}\right) \, .\]- Parameters:
nqubits (int) – number of qubits.
dense (bool) – If
Trueit creates the Hamiltonian as aqibo.core.hamiltonians.Hamiltonian, otherwise it creates aqibo.core.hamiltonians.SymbolicHamiltonian.adj_matrix (list[list[float]] | np.ndarray) – Adjecency matrix of the graph. Defaults to a homogeneous fully connected graph with all edges having an equal 1.0 weight.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
LABS#
- class qibo.hamiltonians.LABS(nqubits: int, dense: bool = True, backend: Backend | None = None)[source]#
Create Hamiltonian of the Low Autocorrelation Binary Sequences (LABS) problem.
Given an integer \(n > 2\), the LABS problem consists of finding a binary sequence \(b \in \{0, \, 1\}^{n}\) the minimizes the sidelobe energy \(E(b)\) defined as
\[E(b) = \sum_{j=1}^{n-1} \, C_{j}^{2}(b) \, ; \quad C_{j}(b) = \sum_{k=0}^{n-j} \, b_{k} \, b_{k + j} \, ,\]where \(C_{j}(b)\) is the \(j\)-th autocorrelation of \(b\).
- Parameters:
nqubits (int) – Total number of qubits.
dense (bool) – If
Trueit creates the Hamiltonian as aqibo.core.hamiltonians.Hamiltonian, otherwise it creates aqibo.core.hamiltonians.SymbolicHamiltonian.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
References
1. T. Packebusch and S. Mertens, Low autocorrelation binary sequences, J. Phys. A: Math. Theor. 49 (2016) 165001.
Heisenberg model#
- class qibo.hamiltonians.Heisenberg(nqubits, coupling_constants: float | int | list | tuple, external_field_strengths: float | int, dense: bool = True, backend=None)[source]#
Heisenberg model on a \(1\)-dimensional periodic lattice.
The general \(n\)-qubit Hamiltonian is given by
\[\begin{split}\begin{align} H &= -\sum_{k = 1}^{n} \, \left( J_{x} \, X_{k} \, X_{k + 1} + J_{y} \, Y_{k} \, Y_{k + 1} + J_{z} \, Z_{k} \, Z_{k + 1} \right) \\ &\quad\,\, - \sum_{k = 1}^{n} \left( h_{x} \, X_{k} + h_{y} \, Y_{k} + h_{z} \, Z_{k} \right) \, , \end{align}\end{split}\]where \(\{J_{x}, \, J_{y}, \, J_{z}\}\) are called the
coupling constants, \(\{h_{x}, \, h_{y}, \, h_{z}\}\) are called theexternal field strengths, and \(\{X, \, Y, \, Z\}\) are the usual Pauli operators.- Parameters:
nqubits (int) – number of qubits.
coupling_constants (list or tuple or float or int) – list or tuple with the three coupling constants \(\{J_{x}, J_{y}, J{z}\}\). If
intorfloat, then \(J_{x} = J_{y} = J_{z}\).external_field_strength (list or tuple or float or int) – list or tuple with the external magnetic field strengths \(\{h_{x}, \, h_{y}, \, h_{z}\}\). If
intorfloat, then \(h_{x} = h_{y} = h_{z}\).dense (bool, optional) – If
True, creates the Hamiltonian as aqibo.core.hamiltonians.Hamiltonian, otherwise it creates aqibo.core.hamiltonians.SymbolicHamiltonian. Defaults toTrue.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Heisenberg Hamiltonian.
- Return type:
qibo.hamiltonians.Hamiltonianorqibo.hamiltonians.SymbolicHamiltonian
Heisenberg XXX#
- class qibo.hamiltonians.XXX(nqubits, coupling_constant: float | int = 1, external_field_strengths: float | int | list | tuple = [0.5, 0, 0], dense: bool = True, backend=None)[source]#
Heisenberg \(\mathrm{XXX}\) model with periodic boundary conditions.
The \(n\)-qubit \(\mathrm{XXX}\) Hamiltonian is given by
\[H = -J \, \sum_{k = 1}^{n} \, \left( X_{k} \, X_{k + 1} + Y_{k} \, Y_{k + 1} + Z_{k} \, Z_{k + 1} \right) - \sum_{k = 1}^{n} \left(h_{x} \, X_{k} + h_{y} \, Y_{k} + h_{z} \, Z_{k} \right) \, ,\]where \(J\) is the
coupling_constant, \(\{h_{x}, \, h_{y}, \, h_{z}\}\) are called theexternal field strengths, and \(\{X, \, Y, \, Z\}\) are the usual Pauli operators.- Parameters:
nqubits (int) – number of qubits.
coupling_constant (float or int, optional) – coupling constant \(J\). Defaults to \(1\).
external_field_strengths (float or int or list or tuple, optional) – list or tuple with the external magnetic field strengths \(\{h_{x}, \, h_{y}, \, h_{z}\}\). If
intorfloat, then \(h_{x} = h_{y} = h_{z}\). Defaults to \([1/2, \, 0, \, 0]\).dense (bool, optional) – If
True, creates the Hamiltonian as aqibo.core.hamiltonians.Hamiltonian, otherwise it creates aqibo.core.hamiltonians.SymbolicHamiltonian. Defaults toTrue.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Heisenberg \(\mathrm{XXX}\) Hamiltonian.
- Return type:
qibo.hamiltonians.Hamiltonianorqibo.hamiltonians.SymbolicHamiltonian
Heisenberg XXZ#
- class qibo.hamiltonians.XXZ(nqubits, delta=0.5, dense: bool = True, backend=None)[source]#
Heisenberg \(\mathrm{XXZ}\) model with periodic boundary conditions.
\[H = \sum _{k=0}^N \, \left( X_{k} \, X_{k + 1} + Y_{k} \, Y_{k + 1} + \delta Z_{k} \, Z_{k + 1} \right) \, .\]Example
from qibo.hamiltonians import XXZ h = XXZ(3) # initialized XXZ model with 3 qubits
- Parameters:
nqubits (int) – number of qubits.
delta (float, optional) – coefficient for the \(Z\) component. Defaults to \(0.5\).
dense (bool, optional) – If
True, creates the Hamiltonian as aqibo.core.hamiltonians.Hamiltonian, otherwise it creates aqibo.core.hamiltonians.SymbolicHamiltonian. Defaults toTrue.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Heisenberg \(\mathrm{XXZ}\) Hamiltonian.
- Return type:
qibo.hamiltonians.Hamiltonianorqibo.hamiltonians.SymbolicHamiltonian
Note
All pre-coded Hamiltonians can be created as
qibo.hamiltonians.Hamiltonian using dense=True
or qibo.hamiltonians.SymbolicHamiltonian
using the dense=False. In the first case the Hamiltonian is created
using its full matrix representation of size (2 ** n, 2 ** n)
where n is the number of qubits that the Hamiltonian acts on. This
matrix is used to calculate expectation values by direct matrix multiplication
to the state and for time evolution by exact exponentiation.
In contrast, when dense=False the Hamiltonian contains a more compact
representation as a sum of local terms. This compact representation can be
used to calculate expectation values via a sum of the local term expectations
and time evolution via the Trotter decomposition of the evolution operator.
This is useful for systems that contain many qubits for which constructing
the full matrix is intractable.
Symbols#
Qibo provides a basic set of symbols which inherit the sympy.Symbol object
and can be used to construct qibo.hamiltonians.SymbolicHamiltonian
objects as described in the previous section.
- class qibo.symbols.Symbol(q, matrix, name='Symbol', commutative=False, **assumptions)[source]#
Qibo specialization for
sympysymbols.These symbols can be used to create
qibo.hamiltonians.hamiltonians.SymbolicHamiltonian. See How to define custom Hamiltonians using symbols? for more details.Example
from qibo import hamiltonians from qibo.symbols import X, Y, Z # construct a XYZ Hamiltonian on two qubits using Qibo symbols form = X(0) * X(1) + Y(0) * Y(1) + Z(0) * Z(1) ham = hamiltonians.SymbolicHamiltonian(form)
- Parameters:
q (int) – Target qubit id.
matrix (np.ndarray) – 2x2 matrix represented by this symbol.
name (str) – Name of the symbol which defines how it is represented in symbolic expressions.
commutative (bool) – If
Truethe constructed symbols commute with each other. Default isFalse. This argument should be used with caution because quantum operators are not commutative objects and therefore switching this toTruemay lead to wrong results. It is useful for improving performance in symbolic calculations in cases where the user is sure that the operators participating in the Hamiltonian form are commuting (for example when the Hamiltonian consists of Z terms only).
- property gate#
Qibo gate that implements the action of the symbol on states.
- class qibo.symbols.I(q, commutative=False, **assumptions)[source]#
Qibo symbol for the identity operator.
- Parameters:
q (int) – Target qubit id.
- class qibo.symbols.X(q, commutative=False, **assumptions)[source]#
Qibo symbol for the Pauli-X operator.
- Parameters:
q (int) – Target qubit id.
- class qibo.symbols.Y(q, commutative=False, **assumptions)[source]#
Qibo symbol for the Pauli-X operator.
- Parameters:
q (int) – Target qubit id.
- class qibo.symbols.Z(q, commutative=False, **assumptions)[source]#
Qibo symbol for the Pauli-X operator.
- Parameters:
q (int) – Target qubit id.
Execution Outcomes#
Qibo circuits return different objects when executed depending on what the circuit contains and on the settings of the simulation. The following table summarizes which outcomes to expect depending on whether:
the circuit contains noise channels
the qubits are measured at the end of the execution
some collapse measurement is present in the circuit
density_matrixis set toTruein simulation
Noise |
Measurements |
Collapse |
Density Matrix |
Outcome |
|---|---|---|---|---|
❌ |
❌ |
❌ |
❌ / ✅ |
|
❌ |
✅ |
❌ |
❌ / ✅ |
|
❌ / ✅ |
❌ |
❌ / ✅ |
✅ |
|
❌ / ✅ |
✅ |
❌ / ✅ |
❌ |
|
❌ / ✅ |
✅ |
❌ / ✅ |
✅ |
Therefore, one of the three objects qibo.result.QuantumState,
qibo.result.MeasurementOutcomes or qibo.result.CircuitResult
is going to be returned by the circuit execution. The first gives acces to the final
state and probabilities via the qibo.result.QuantumState.state() and
qibo.result.QuantumState.probabilities() methods, whereas the second
allows to retrieve the final samples, the frequencies and the probabilities (calculated
as frequencies/nshots) with the qibo.result.MeasurementOutcomes.samples(),
qibo.result.MeasurementOutcomes.frequencies() and
qibo.result.MeasurementOutcomes.probabilities() methods respectively. The
qibo.result.CircuitResult object includes all the above instead.
Every time some measurement is performed at the end of the execution, the result
will be a CircuitResult unless the final state could not be represented with the
current simulation settings, i.e. if some stochasticity is present in the ciruit
(via noise channels or collapse measurements) and density_matrix=False. In that
case a simple MeasurementOutcomes object is returned.
If no measurement is appended at the end of the circuit, the final QuantumState
is going to be provided as output. However, if the circuit is stochastic,
density_matrix should be set to True in order to recover the final state,
otherwise an error is raised.
The final result of the circuit execution can also be saved to disk and loaded back:
circuit = Circuit(2)
circuit.add(gates.M(0,1))
# this will be a CircuitResult object
result = circuit()
# save it to final_result.npy
result.dump('final_result.npy')
# can be loaded back
from qibo.result import load_result
loaded_result = load_result('final_result.npy')
- class qibo.result.QuantumState(state, backend=None)[source]#
Data structure to represent the final state after circuit execution.
- Parameters:
state (np.ndarray) – Input quantum state as np.ndarray.
backend (qibo.backends.AbstractBackend) – Backend used for the calculations. If not provided, the current backend is going to be used.
- symbolic(decimals: int = 5, cutoff: float = 1e-10, max_terms: int = 20)[source]#
Dirac notation representation of the state in the computational basis.
- Parameters:
decimals (int, optional) – Number of decimals for the amplitudes. Defaults to \(5\).
cutoff (float, optional) – Amplitudes with absolute value smaller than the cutoff are ignored from the representation. Defaults to
1e-10.max_terms (int, optional) – Maximum number of terms to print. If the state contains more terms they will be ignored. Defaults to \(20\).
- Returns:
A string representing the state in the computational basis.
- Return type:
(str)
- state(numpy: bool = False)[source]#
State’s tensor representation as a backend tensor.
Note
If the state has Hamming weight \(k\) and is computed using the
HammingWeightBackend, its dimension is \(d = \binom{n}{k}\), where \(n\) is the number of qubits.- Parameters:
numpy (bool, optional) – If
Truethe returned tensor will be anumpyarray, otherwise it will follow the backend tensor type. Defaults toFalse.- Returns:
The state in the computational basis.
- probabilities(qubits: list | set | None = None)[source]#
Calculates measurement probabilities by tracing out qubits.
When noisy model is applied to a circuit and circuit.density_matrix=False, this method returns the average probability resulting from repeated execution. This probability distribution approximates the exact probability distribution obtained when circuit.density_matrix=True.
- to_dict()[source]#
Returns a dictonary containinig all the information needed to rebuild the
QuantumState
- dump(filename: str)[source]#
Writes to file the
QuantumStatefor future reloading.- Parameters:
filename (str) – Path to the file to write to.
- classmethod from_dict(payload: dict)[source]#
Builds a
QuantumStateobject starting from a dictionary.- Parameters:
payload (dict) – Dictionary containing all the information to load the
QuantumStateobject.- Returns:
Quantum state object..
- Return type:
- class qibo.result.MeasurementOutcomes(measurements, backend=None, probabilities=None, samples: int | None = None, nshots: int = 1000)[source]#
Object to store the outcomes of measurements after circuit execution.
- Parameters:
measurements (
qibo.gates.M) – Measurement gates.backend (
qibo.backends.AbstractBackend) – Backend used for the calculations. IfNone, then the current backend is used. Defaults toNone.probabilities (np.ndarray) – Use these probabilities to generate samples and frequencies.
samples (np.darray) – Use these samples to generate probabilities and frequencies.
nshots (int) – Number of shots used for samples, probabilities and frequencies generation.
- frequencies(binary: bool = True, registers: bool = False)[source]#
Returns the frequencies of measured samples.
- Parameters:
- Returns:
A
collections.Counterwhere the keys are the observed values and the values the corresponding frequencies, that is the number of times each measured value/bitstring appears.- If
binaryisTrue the keys of the
collections.Counterare in binary form, as strings of \(0\) and :math`1`.- If
binaryisFalse the keys of the
collections.Counterare integers.- If
registersisTrue a dict of
collections.Counteris returned where keys are the name of each register.- If
registersisFalse a single
collections.Counteris returned which contains samples from all the measured qubits, independently of their registers.
- If
- probabilities(qubits: list | set | None = None)[source]#
Calculate the probabilities as frequencies / nshots
- Returns:
The array containing the probabilities of the measured qubits.
- has_samples()[source]#
Check whether the samples are available already.
- Returns:
Trueif the samples are available,Falseotherwise.- Return type:
(bool)
- samples(binary: bool = True, registers: bool = False)[source]#
Returns raw measurement samples.
- Parameters:
- Returns:
- If
binaryisTrue samples are returned in binary form as a tensor of shape
(nshots, n_measured_qubits).- If
binaryisFalse samples are returned in decimal form as a tensor of shape
(nshots,).- If
registersisTrue samples are returned in a
dictwhere the keys are the register names and the values are the samples tensors for each register.- If
registersisFalse a single tensor is returned which contains samples from all the measured qubits, independently of their registers.
- If
- property measurement_gate#
Single measurement gate containing all measured qubits.
Useful for sampling all measured qubits at once when simulating.
- apply_bitflips(p0: float, p1: float | None = None)[source]#
Apply bitflips to the measurements with probabilities p0 and p1
- expectation_from_samples(observable)[source]#
Computes the real expectation value of a diagonal observable from frequencies.
- Parameters:
observable (Hamiltonian/SymbolicHamiltonian) – diagonal observable in the computational basis.
- Returns:
expectation value from samples.
- Return type:
(float)
- to_dict()[source]#
Returns a dictonary containinig all the information needed to rebuild the
qibo.result.MeasurementOutcomes.
- dump(filename: str)[source]#
Writes to file the
qibo.result.MeasurementOutcomesfor future reloading.- Parameters:
filename (str) – Path to the file to write to.
- classmethod from_dict(payload: dict)[source]#
Builds a
qibo.result.MeasurementOutcomesobject starting from a dictionary.- Parameters:
payload (dict) – Dictionary containing all the information to load the
qibo.result.MeasurementOutcomesobject.- Returns:
A
qibo.result.MeasurementOutcomesobject.
- classmethod load(filename: str)[source]#
Builds the
qibo.result.MeasurementOutcomesobject stored in a file.- Parameters:
filename (str) – Path to the file containing the
qibo.result.MeasurementOutcomes.- Returns:
A
qibo.result.MeasurementOutcomesobject.
- class qibo.result.CircuitResult(final_state, measurements, backend=None, samples=None, nshots=1000)[source]#
Object to store both the outcomes of measurements and the final state after circuit execution.
- Parameters:
final_state (np.ndarray) – Input quantum state as np.ndarray.
measurements (qibo.gates.M) – The measurement gates containing the measurements.
backend (qibo.backends.AbstractBackend) – Backend used for the calculations. If not provided, then the current backend is going to be used.
probabilities (np.ndarray) – Use these probabilities to generate samples and frequencies.
samples (np.darray) – Use these samples to generate probabilities and frequencies.
nshots (int) – Number of shots used for samples, probabilities and frequencies generation.
- probabilities(qubits: list | set | None = None)[source]#
Calculates measurement probabilities by tracing out qubits.
When noisy model is applied to a circuit and circuit.density_matrix=False, this method returns the average probability resulting from repeated execution. This probability distribution approximates the exact probability distribution obtained when circuit.density_matrix=True.
- to_dict()[source]#
Returns a dictonary containinig all the information needed to rebuild the
CircuitResult.
Callbacks#
Callbacks provide a way to calculate quantities on the state vector as it
propagates through the circuit. Example of such quantity is the entanglement
entropy, which is currently the only callback implemented in
qibo.callbacks.EntanglementEntropy.
The user can create custom callbacks by inheriting the
qibo.callbacks.Callback class. The point each callback is
calculated inside the circuit is defined by adding a qibo.gates.CallbackGate.
This can be added similarly to a standard gate and does not affect the state vector.
- class qibo.callbacks.Callback[source]#
Base callback class.
Results of a callback can be accessed by indexing the corresponding object.
- property nqubits#
Total number of qubits in the circuit that the callback was added in.
Entanglement entropy#
- class qibo.callbacks.EntanglementEntropy(partition: List[int] | None = None, compute_spectrum: bool = False, base: float = 2)[source]#
Von Neumann entanglement entropy callback.
\[S = \mathrm{Tr} \left ( \rho \log _2 \rho \right )\]- Parameters:
Example
from qibo import Circuit, gates from qibo.callbacks import EntanglementEntropy # create entropy callback where qubit 0 is the first subsystem entropy = EntanglementEntropy([0], compute_spectrum=True) # initialize circuit with 2 qubits and add gates circuit = Circuit(2) # add callback gates between normal gates circuit.add(gates.CallbackGate(entropy)) circuit.add(gates.H(0)) circuit.add(gates.CallbackGate(entropy)) circuit.add(gates.CNOT(0, 1)) circuit.add(gates.CallbackGate(entropy)) # execute the circuit final_state = circuit() print(entropy[:]) # Should print [0, 0, 1] which is the entanglement entropy # after every gate in the calculation. print(entropy.spectrum) # Print the entanglement spectrum.
- property nqubits#
Total number of qubits in the circuit that the callback was added in.
Norm#
Overlap#
- class qibo.callbacks.Overlap(state)[source]#
State overlap callback.
Calculates the overlap between the circuit state and a given target state:
\[\mathrm{Overlap} = |\left \langle \Phi | \Psi \right \rangle |\]- Parameters:
state (np.ndarray) – Target state to calculate overlap with.
normalize (bool) – If
Truethe states are normalized for the overlap calculation.
Energy#
- class qibo.callbacks.Energy(hamiltonian: hamiltonians.Hamiltonian)[source]#
Energy expectation value callback.
Calculates the expectation value of a given Hamiltonian as:
\[\left \langle H \right \rangle = \left \langle \Psi | H | \Psi \right \rangle = \mathrm{Tr} (\rho H)\]assuming that the state is normalized.
- Parameters:
hamiltonian (
qibo.hamiltonians.Hamiltonian) – Hamiltonian object to calculate its expectation value.
Gap#
- class qibo.callbacks.Gap(mode: str | int = 'gap', check_degenerate: bool = True)[source]#
Callback for calculating the gap of adiabatic evolution Hamiltonians.
Can also be used to calculate the Hamiltonian eigenvalues at each time step during the evolution. Note that this callback can only be added in
qibo.evolution.AdiabaticEvolutionmodels.- Parameters:
mode (str/int) – Defines which quantity this callback calculates. If
mode == 'gap'then the difference between ground state and first excited state energy (gap) is calculated. Ifmodeis an integer, then the energy of the corresponding eigenstate is calculated.check_degenerate (bool) – If
Truethe excited state number is increased until a non-zero gap is found. This is used to find the proper gap in the case of degenerate Hamiltonians. This flag is relevant only ifmodeis'gap'. Default isTrue.
Example
from qibo import callbacks, hamiltonians from qibo.models import AdiabaticEvolution # define easy and hard Hamiltonians for adiabatic evolution h0 = hamiltonians.X(3) h1 = hamiltonians.TFIM(3, h=1.0) # define callbacks for logging the ground state, first excited # and gap energy ground = callbacks.Gap(0) excited = callbacks.Gap(1) gap = callbacks.Gap() # define and execute the ``AdiabaticEvolution`` model evolution = AdiabaticEvolution(h0, h1, lambda t: t, dt=1e-1, callbacks=[gap, ground, excited]) final_state = evolution(final_time=1.0) # print results print(ground[:]) print(excited[:]) print(gap[:])
Solvers#
Solvers are used to numerically calculate the time evolution of state vectors. They perform steps in time by integrating the time-dependent Schrodinger equation.
- class qibo.solvers.BaseSolver(dt, hamiltonian)[source]#
Basic solver that should be inherited by all solvers.
- Parameters:
dt (float) – Time step size.
hamiltonian (
qibo.hamiltonians.abstract.AbstractHamiltonian) – Hamiltonian object that the state evolves under.
- property t#
Solver’s current time.
- class qibo.solvers.TrotterizedExponential(dt, hamiltonian)[source]#
Solver that uses Trotterized exponentials.
Created automatically from the
qibo.solvers.Exponentialif the given Hamiltonian object is aqibo.hamiltonians.hamiltonians.SymbolicHamiltonian.
- class qibo.solvers.Exponential(dt, hamiltonian)[source]#
Solver that uses the matrix exponential of the Hamiltonian:
\[U(t) = e^{-i H(t) \delta t}\]Calculates the evolution operator in every step and thus is compatible with time-dependent Hamiltonians.
Optimizers#
Optimizers are used automatically by the minimize methods of
qibo.models.VQE and qibo.evolution.AdiabaticEvolution models.
The user does not have to use any of the optimizer methods included in the
current section, however the required options of each optimization method
can be passed when calling the minimize method of the respective Qibo
variational model.
- qibo.optimizers.optimize(loss, initial_parameters, args=(), method='Powell', jac=None, hess=None, hessp=None, bounds=None, constraints=(), tol=None, callback=None, options=None, compile=False, processes=None, backend=None)[source]#
- Main optimization method. Selects one of the following optimizers:
- Parameters:
loss (callable) – Loss as a function of
parametersand optional extra arguments. Make sure the loss function returns a tensor formethod=sgdand numpy object for all the other methods.initial_parameters (np.ndarray) – Initial guess for the variational parameters that are optimized.
args (tuple) – optional arguments for the loss function.
method (str) – Name of optimizer to use. Can be
'cma','sgd'or one of the Newtonian methods supported byqibo.optimizers.newtonian()and'parallel_L-BFGS-B'.sgdis only available for backends based on tensorflow.jac (dict) – Method for computing the gradient vector for scipy optimizers.
hess (dict) – Method for computing the hessian matrix for scipy optimizers.
hessp (callable) – Hessian of objective function times an arbitrary vector for scipy optimizers.
bounds (sequence or Bounds) – Bounds on variables for scipy optimizers.
constraints (dict) – Constraints definition for scipy optimizers.
tol (float) – Tolerance of termination for scipy optimizers.
callback (callable) – Called after each iteration for scipy optimizers.
options (dict) – Dictionary with options. See the specific optimizer bellow for a list of the supported options.
compile (bool) – If
Truethe Tensorflow optimization graph is compiled. This is relevant only for the'sgd'optimizer.processes (int) – number of processes when using the parallel BFGS method.
- Returns:
Final best loss value; best parameters obtained by the optimizer; extra: optimizer-specific return object. For scipy methods it returns the
OptimizeResult, for'cma'theCMAEvolutionStrategy.result, and for'sgd'the options used during the optimization.- Return type:
Example
import numpy as np from qibo import Circuit, gates from qibo.optimizers import optimize # create custom loss function # make sure the return type matches the optimizer requirements. def myloss(parameters, circuit): circuit.set_parameters(parameters) return np.square(np.sum(circuit().state())) # returns numpy array # create circuit ansatz for two qubits circuit = Circuit(2) circuit.add(gates.RY(0, theta=0)) # optimize using random initial variational parameters initial_parameters = np.random.uniform(0, 2, 1) best, params, extra = optimize(myloss, initial_parameters, args=(circuit)) # set parameters to circuit circuit.set_parameters(params)
- qibo.optimizers.cmaes(loss, initial_parameters, args=(), callback=None, options=None)[source]#
Genetic optimizer based on pycma.
- Parameters:
loss (callable) – Loss as a function of variational parameters to be optimized.
initial_parameters (np.ndarray) – Initial guess for the variational parameters.
args (tuple) – optional arguments for the loss function.
callback (list[callable]) – List of callable called after each optimization iteration. According to cma-es implementation take
CMAEvolutionStrategyinstance as argument. See: https://cma-es.github.io/apidocs-pycma/cma.evolution_strategy.CMAEvolutionStrategy.html.options (dict) – Dictionary with options accepted by the
cmaoptimizer. The user can useimport cma; cma.CMAOptions()to view the available options.
- qibo.optimizers.newtonian(loss, initial_parameters, args=(), method='Powell', jac=None, hess=None, hessp=None, bounds=None, constraints=(), tol=None, callback=None, options=None, processes=None, backend=None)[source]#
Newtonian optimization approaches based on
scipy.optimize.minimize.For more details check the scipy documentation.
Note
When using the method
parallel_L-BFGS-Btheprocessesoption controls the number of processes used by the parallel L-BFGS-B algorithm through themultiprocessinglibrary. By defaultprocesses=None, in this case the total number of logical cores are used. Make sure to select the appropriate number of processes for your computer specification, taking in consideration memory and physical cores. In order to obtain optimal results you can control the number of threads used by each process with theqibo.set_threadsmethod. For example, for small-medium size circuits you may benefit from single thread per process, thus setqibo.set_threads(1)before running the optimization.- Parameters:
loss (callable) – Loss as a function of variational parameters to be optimized.
initial_parameters (np.ndarray) – Initial guess for the variational parameters.
args (tuple) – optional arguments for the loss function.
method (str) – Name of method supported by
scipy.optimize.minimizeand'parallel_L-BFGS-B'for a parallel version of L-BFGS-B algorithm.jac (dict) – Method for computing the gradient vector for scipy optimizers.
hess (dict) – Method for computing the hessian matrix for scipy optimizers.
hessp (callable) – Hessian of objective function times an arbitrary vector for scipy optimizers.
bounds (sequence or Bounds) – Bounds on variables for scipy optimizers.
constraints (dict) – Constraints definition for scipy optimizers.
tol (float) – Tolerance of termination for scipy optimizers.
callback (callable) – Called after each iteration for scipy optimizers.
options (dict) – Dictionary with options accepted by
scipy.optimize.minimize.processes (int) – number of processes when using the parallel BFGS method.
- qibo.optimizers.sgd(loss, initial_parameters, args=(), callback=None, options=None, compile=False, backend=None)[source]#
Stochastic Gradient Descent (SGD) optimizer using Tensorflow backpropagation.
See tf.keras.Optimizers for a list of the available optimizers for Tensorflow. See torch.optim for a list of the available optimizers for PyTorch.
- Parameters:
loss (callable) – Loss as a function of variational parameters to be optimized.
initial_parameters (np.ndarray) – Initial guess for the variational parameters.
args (tuple) – optional arguments for the loss function.
callback (callable) – Called after each iteration.
options (dict) –
Dictionary with options for the SGD optimizer. Supports the following keys:
'optimizer'(str, default:'Adagrad'): Name of optimizer.'learning_rate'(float, default:'1e-3'): Learning rate.'nepochs'(int, default:1e6): Number of epochs for optimization.'nmessage'(int, default:1e3): Every how many epochs to print a message of the loss function.
Parameter#
It can be useful to define custom parameters in an optimization context. For
example, the rotational angles which encodes information in a Quantum Neural Network
are usually built as a combination of features and trainable parameters. For
doing this, the qibo.parameter.Parameter class can be used. It allows
to define custom parameters which can be inserted into a qibo.models.circuit.Circuit.
Moreover, it automatically precomputes the analytical derivative of the parameter
function, which can be used to calculate the derivatives of a variational model
with respect to its parameters.
- qibo.parameter.calculate_derivatives(func)[source]#
Calculates derivatives w.r.t. to all parameters of a target function func.
- class qibo.parameter.Parameter(func, trainable=None, features=None)[source]#
Object which allows for variational gate parameters. Several trainable parameters and possibly features are linked through a lambda function which returns the final gate parameter. All possible analytical derivatives of the lambda function are calculated at the object initialisation using Sympy.
Example:
from qibo.parameter import Parameter param = Parameter( lambda x, th1, th2, th3: x**2 * th1 + th2 * th3**2, features=[7.0], trainable=[1.5, 2.0, 3.0], ) partial_derivative = param.get_partial_derivative(3) param.update_parameters(trainable=[15.0, 10.0, 7.0], feature=[5.0]) param_value = param()
- Parameters:
func (function) – lambda function which builds the gate parameter. If both features and trainable parameters compose the function, it must be passed by first providing the features and then the parameters, as described in the code example above.
features (list or np.ndarray) – array containing possible input features x.
trainable (list or np.ndarray) – array with initial trainable parameters theta.
- property nparams#
Returns the number of trainable parameters
- property nfeat#
Returns the number of features
- property ncomponents#
Return the number of elements which compose the Parameter
- trainable_parameter_indices(start_index)[source]#
Return list of respective indices of trainable parameters within the larger trainable parameter list of a circuit for example
Gradients#
In the context of optimization, particularly when dealing with Quantum Machine Learning problems, it is often necessary to calculate the gradients of functions that are to be minimized (or maximized). Hybrid methods, which are based on the use of classical techniques for the optimization of quantum computation procedures, have been presented in the previous section. This approach is very useful in simulation, but some classical methods cannot be used when using real circuits: for example, in the context of neural networks, the Back-Propagation algorithm is used, where it is necessary to know the value of a target function during the propagation of information within the network. Using a real circuit, we would not be able to access this information without taking a measurement, causing the state of the system to collapse and losing the information accumulated up to that moment. For this reason, in qibo we have also implemented methods for calculating the gradients which can be performed directly on the hardware, such as the Parameter Shift Rule.
- qibo.derivative.parameter_shift(circuit, hamiltonian, parameter_index, initial_state=None, scale_factor=1, nshots=None)[source]#
In this method the parameter shift rule (PSR) is implemented. Given a circuit \(U\) and an observable \(H\), the PSR allows to calculate the derivative of the expected value of \(H\) on the final state with respect to a variational parameter of the circuit. There is also the possibility of setting a scale factor. It is useful when a circuit’s parameter is obtained by combination of a variational parameter and an external object, such as a training variable in a Quantum Machine Learning problem. For example, performing a re-uploading strategy to embed some data into a circuit, we apply to the quantum state rotations whose angles are in the form \(\theta^{\prime} = x \, \theta\), where \(\theta\) is a variational parameter, and \(x\) an input variable. The PSR allows to calculate the derivative with respect to \(\theta^{\prime}\). However, if we want to optimize a system with respect to its variational parameters, we need to “free” this procedure from the \(x\) depencency. If the
scale_factoris not provided, it is set equal to one and doesn’t affect the calculation. If the PSR is needed to be executed on a real quantum device, it is important to setnshotsto some integer value. This enables the execution on the hardware by calling the proper methods.- Parameters:
circuit (
qibo.models.circuit.Circuit) – custom quantum circuit.hamiltonian (
qibo.hamiltonians.Hamiltonian) – target observable. if you want to execute on hardware, a symbolic hamiltonian must be provided as follows (example with Pauli-\(Z\) and \(n = 1\)):SymbolicHamiltonian(np.prod([ Z(i) for i in range(1) ])).parameter_index (int) – the index which identifies the target parameter in the
circuit.get_parameters()list.initial_state (ndarray, optional) – initial state on which the circuit acts. If
None, defaults to the zero state \(\ket{\mathbf{0}}\). Defaults toNone.scale_factor (float, optional) – parameter scale factor. Defaults to \(1\).
nshots (int, optional) – number of shots if derivative is evaluated on hardware. If
None, the simulation mode is executed. Defaults toNone.
- Returns:
- Value of the derivative of the expectation value of the hamiltonian
with respect to the target variational parameter.
- Return type:
Example
import qibo import numpy as np from qibo import Circuit, gates, hamiltonians from qibo.derivative import parameter_shift # defining an observable def hamiltonian(nqubits = 1): m0 = (1/nqubits)*hamiltonians.Z(nqubits).matrix ham = hamiltonians.Hamiltonian(nqubits, m0) return ham # defining a dummy circuit def circuit(nqubits = 1): c = Circuit(nqubits = 1) c.add(gates.RY(q = 0, theta = 0)) c.add(gates.RX(q = 0, theta = 0)) c.add(gates.M(0)) return c # initializing the circuit c = circuit(nqubits = 1) # some parameters test_params = np.random.randn(2) c.set_parameters(test_params) test_hamiltonian = hamiltonian() # running the psr with respect to the two parameters grad_0 = parameter_shift(circuit=c, hamiltonian=test_hamiltonian, parameter_index=0) grad_1 = parameter_shift(circuit=c, hamiltonian=test_hamiltonian, parameter_index=1)
- qibo.derivative.finite_differences(circuit, hamiltonian, parameter_index, initial_state=None, step_size=1e-07)[source]#
Calculate derivative of the expectation value of
hamiltonianon the final state obtained by executingcircuitoninitial_statewith respect to the variational parameter identified byparameter_indexin the circuit’s parameters list. This method can be used only in exact simulation mode.- Parameters:
circuit (
qibo.models.circuit.Circuit) – custom quantum circuit.hamiltonian (
qibo.hamiltonians.Hamiltonian) – target observable. To execute on hardware, a symbolic hamiltonian must be provided as follows (example with Pauli-\(Z\) and \(n = 1\)):SymbolicHamiltonian(np.prod([ Z(i) for i in range(1) ])).parameter_index (int) – the index which identifies the target parameter in the
qibo.models.Circuit.get_parameters()list.initial_state (ndarray, optional) – initial state on which the circuit acts. If
None, defaults to the zero state \(\ket{\mathbf{0}}\). Defaults toNone.step_size (float, optional) – step size used to evaluate the finite difference. Defaults to \(10^{-7}\).
- Returns:
- Value of the derivative of the expectation value of the hamiltonian
with respect to the target variational parameter.
- Return type:
Quantum Information#
This module provides tools for generation and analysis of quantum (and classical) information.
Basis#
Set of functions related to basis and basis transformations.
Pauli basis#
- qibo.quantum_info.pauli_basis(nqubits: int, normalize: bool = False, vectorize: bool = False, sparse: bool = False, order: str | None = None, pauli_order: str = 'IXYZ', backend: Backend | None = None)[source]#
Creates the
nqubits-qubit Pauli basis.- Parameters:
nqubits (int) – number of qubits.
normalize (bool, optional) – If
True, normalized basis is returned. Defaults to False.vectorize (bool, optional) – If
False, returns a nested array with all Pauli matrices. IfTrue, retuns an array where every row is a vectorized Pauli matrix. Defaults toFalse.sparse (bool, optional) – If
True, retuns Pauli basis in a sparse representation. Defaults toFalse.order (str, optional) – If
"row", vectorization of Pauli basis is performed row-wise. If"column", vectorization is performed column-wise. If"system", system-wise vectorization is performed. Ifvectorization=False, thenorder=Noneis forced. Defaults toNone.pauli_order (str, optional) – corresponds to the order of 4 single-qubit Pauli elements. Defaults to
"IXYZ".backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
- all Pauli matrices forming the basis. If
sparse=True and
vectorize=True, tuple is composed of an array of non-zero elements and an array with their row-wise indexes.
- all Pauli matrices forming the basis. If
- Return type:
ndarray or tuple
Computational basis to Pauli basis#
- qibo.quantum_info.comp_basis_to_pauli(nqubits: int, normalize: bool = False, sparse: bool = False, order: str = 'row', pauli_order: str = 'IXYZ', backend=None)[source]#
Unitary matrix \(U\) that converts operators from the Liouville representation in the computational basis to the Pauli-Liouville representation.
The unitary \(U\) is given by
\[U = \sum_{k = 0}^{d^{2} - 1} \, |k)(P_{k}| \,\, ,\]where \(|P_{k})\) is the vectorization of the \(k\)-th Pauli operator \(P_{k}\), and \(|k)\) is the vectorization of the \(k\)-th computational basis element. For a definition of vectorization, see
qibo.quantum_info.vectorization().Example
from qibo.quantum_info import random_density_matrix, vectorization, comp_basis_to_pauli nqubits = 2 d = 2**nqubits rho = random_density_matrix(d) U_c2p = comp_basis_to_pauli(nqubits) rho_liouville = vectorization(rho, order="system") rho_pauli_liouville = U_c2p @ rho_liouville
- Parameters:
nqubits (int) – number of qubits.
normalize (bool, optional) – If
True, converts to the Pauli basis. Defaults toFalse.sparse (bool, optional) – If
True, returns unitary matrix in sparse representation. Defaults toFalse.order (str, optional) – If
"row", vectorization of Pauli basis is performed row-wise. If"column", vectorization is performed column-wise. If"system", system-wise vectorization is performed. Defaults to"row".pauli_order (str, optional) – corresponds to the order of 4 single-qubit Pauli elements. Defaults to
"IXYZ".backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
- Unitary matrix \(U\). If
sparse=True, tuple is composed of array of non-zero elements and an array with their row-wise indexes.
- Unitary matrix \(U\). If
- Return type:
ndarray or tuple
Pauli basis to computational basis#
- qibo.quantum_info.pauli_to_comp_basis(nqubits: int, normalize: bool = False, sparse: bool = False, order: str = 'row', pauli_order: str = 'IXYZ', backend=None)[source]#
Unitary matrix \(U\) that converts operators from the Pauli-Liouville representation to the Liouville representation in the computational basis.
The unitary \(U\) is given by
\[U = \sum_{k = 0}^{d^{2} - 1} \, |P_{k})(b_{k}| \, ,\]where \(|P_{k})\) is the vectorization of the \(k\)-th Pauli operator \(P_{k}\), and \(|k)\) is the vectorization of the \(k\)-th computational basis element. For a definition of vectorization, see
qibo.quantum_info.vectorization().- Parameters:
nqubits (int) – number of qubits.
normalize (bool, optional) – If
True, converts to the Pauli basis. Defaults toFalse.sparse (bool, optional) – If
True, returns unitary matrix in sparse representation. Defaults toFalse.order (str, optional) – If
"row", vectorization of Pauli basis is performed row-wise. If"column", vectorization is performed column-wise. If"system", system-wise vectorization is performed. Defaults to"row".pauli_order (str, optional) – corresponds to the order of 4 single-qubit Pauli elements. Defaults to
"IXYZ".backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
- Unitary matrix \(U\). If
sparse=True, tuple is composed of array of non-zero elements and an array with their row-wise indexes.
- Unitary matrix \(U\). If
- Return type:
ndarray or tuple
Phase-space Representation of Stabilizer States#
A stabilizer state \(\ketbra{\psi}{\psi}\) can be uniquely defined by the set of its stabilizers, i.e. those unitary operators \(U\) that have \(\psi\) as an eigenstate with eigenvalue \(1\). In general, \(n\)-qubit stabilizer states are stabilized by \(d = 2^n\) Pauli operators on said \(n\) qubits. However, it is known that the set of \(d\) Paulis can be generated by only \(n\) unique members of the set. In that case, indeed, the number of operators needed to represent a stabilizer state reduces to \(n\). Each one of these \(n\) Pauli generators takes \(2n + 1\) bits to specify, yielding a \(n(2n+1)\) total number of bits needed. In particular, Aaronson and Gottesman (2004) demonstrated that the application of Clifford gates on stabilizer states can be efficiently simulated in this representation at the cost of storing the generators of the destabilizers, in addition to the stabilizers.
A \(n\)-qubit stabilizer state is uniquely defined by a symplectic matrix of the form

where \((x_{kl},z_{kl})\) are the bits encoding the \(n\)-qubits Pauli generator as
The qibo.quantum_info.clifford.Clifford object is in charge of storing the
phase-space representation of a stabilizer state.
This object is automatically created after the execution of a Clifford circuit through the
qibo.backends.clifford.CliffordBackend, but it can also be created by directly
passing a symplectic matrix to the constructor.
The generators of the stabilizers can be extracted with the
qibo.quantum_info.clifford.Clifford.generators() method,
or the complete set of \(d = 2^{n}\) stabilizers operators can be extracted through the
qibo.quantum_info.clifford.Clifford.stabilizers() method.
generators, phases = clifford.generators()
stabilizers = clifford.stabilizers()
The destabilizers can be extracted analogously with qibo.quantum_info.clifford.Clifford.destabilizers().
We provide integration with the stim package. It is possible to run Clifford circuits using stim as an engine:
from qibo.backends import CliffordBackend
from qibo.quantum_info import Clifford, random_clifford
clifford_backend = CliffordBackend(engine="stim")
circuit = random_clifford(nqubits)
result = clifford_backend.execute_circuit(circuit)
## Note that the execution above is equivalent to the one below
result = Clifford.from_circuit(circuit, engine="stim")
- class qibo.quantum_info.clifford.Clifford(data: ndarray | Circuit, nqubits: int | None = None, measurements: list | None = None, nshots: int = 1000, engine: str | None = None, _backend: CliffordBackend | None = None, _samples: int | None = None)[source]#
Object storing the results of a circuit execution with the
qibo.backends.clifford.CliffordBackend.- Parameters:
data (ndarray or
qibo.models.circuit.Circuit) – Ifndarray, it is the symplectic matrix of the stabilizer state in phase-space representation. Ifqibo.models.circuit.Circuit, it is a circuit composed only of Clifford gates and computational-basis measurements.nqubits (int, optional) – number of qubits of the state.
measurements (list, optional) – list of measurements gates
qibo.gates.M. Defaults toNone.nshots (int, optional) – number of shots used for sampling the measurements. Defaults to \(1000\).
engine (str, optional) –
engine to use in the execution of the
qibo.backends.CliffordBackend. It accepts"numpy","numba","cupy", and"stim"(see stim). IfNone, defaults to the corresponding engine from the current backend. Defaults toNone.
- classmethod from_circuit(circuit: Circuit, initial_state: ndarray | None = None, nshots: int = 1000, engine: str | None = None)[source]#
Allows to create a
qibo.quantum_info.clifford.Cliffordobject by executing the input circuit.- Parameters:
circuit (
qibo.models.circuit.Circuit) – Clifford circuit to run.initial_state (ndarray, optional) – symplectic matrix of the initial state. If
None, defaults to the symplectic matrix of the zero state. Defaults toNone.nshots (int, optional) – number of measurement shots to perform if
circuithas measurement gates. Defaults to \(10^{3}\).engine (str, optional) –
engine to use in the execution of the
qibo.backends.CliffordBackend. It accepts"numpy","numba","cupy", and"stim"(see stim). IfNone, defaults to the corresponding engine from the current backend. Defaults toNone.
- Returns:
Object storing the result of the circuit execution.
- Return type:
- to_circuit(algorithm: str | None = 'AG04', **kwargs)[source]#
Converts symplectic matrix into a Clifford circuit.
- Parameters:
algorithm (str, optional) – If
AG04, uses the decomposition algorithm from Aaronson & Gottesman (2004). IfBM20andClifford.nqubits <= 3, uses the decomposition algorithm from Bravyi & Maslov (2020). Defaults toAG04.kwargs (dict, optional) – Additional arguments used to initialize a Circuit object. For details, see the documentation of
qibo.models.circuit.Circuit.
- Returns:
circuit composed of Clifford gates.
- Return type:
- generators(return_array: bool = False)[source]#
Extracts the generators of stabilizers and destabilizers.
- stabilizers(symplectic: bool = False, return_array: bool = False)[source]#
Extracts the stabilizers of the state.
- Parameters:
symplectic (bool, optional) – If
True, returns the rows of the symplectic matrix that correspond to the \(n\) generators of the \(2^{n}\) total stabilizers, independently ofreturn_array.return_array (bool, optional) – To be used when
symplectic = False. IfTruereturns the stabilizers asndarray. IfFalse, returns stabilizers as strings. Defaults toFalse.
- Returns:
Stabilizers of the state.
- Return type:
(ndarray or list)
- destabilizers(symplectic: bool = False, return_array: bool = False)[source]#
Extracts the destabilizers of the state.
- Parameters:
symplectic (bool, optional) – If
True, returns the rows of the symplectic matrix that correspond to the \(n\) generators of the \(2^{n}\) total destabilizers, independently ofreturn_array.return_array (bool, optional) – To be used when
symplectic = False. IfTruereturns the destabilizers asndarray. IfFalse, their representation as strings is returned. Defaults toFalse.
- Returns:
Destabilizers of the state.
- Return type:
(ndarray or list)
- state()[source]#
Builds the density matrix representation of the state.
Note
This method is inefficient in runtime and memory for a large number of qubits.
- Returns:
Density matrix of the state.
- Return type:
(ndarray)
- property measurement_gate#
Single measurement gate containing all measured qubits.
Useful for sampling all measured qubits at once when simulating.
- samples(binary: bool = True, registers: bool = False)[source]#
Returns raw measurement samples.
- Parameters:
- Returns:
- If
binaryisTrue samples are returned in binary form as a tensor of shape
(nshots, n_measured_qubits).- If
binaryisFalse samples are returned in decimal form as a tensor of shape
(nshots,).- If
registersisTrue samples are returned in a
dictwhere the keys are the register names and the values are the samples tensors for each register.- If
registersisFalse a single tensor is returned which contains samples from all the measured qubits, independently of their registers.
- If
- frequencies(binary: bool = True, registers: bool = False)[source]#
Returns the frequencies of measured samples.
- Parameters:
- Returns:
A collections.Counter where the keys are the observed values and the values the corresponding frequencies, that is the number of times each measured value/bitstring appears.
- If
binaryisTrue the keys of the
collections.Counterare in binary form, as strings of \(0\) and :math`1`.- If
binaryisFalse the keys of the
collections.Counterare integers.- If
registersisTrue a dict of
collections.Counteris returned where keys are the name of each register.- If
registersisFalse a single
collections.Counteris returned which contains samples from all the measured qubits, independently of their registers.
- If
- probabilities(qubits: tuple | list | None = None)[source]#
Computes the probabilities of the selected qubits from the measured samples.
- copy(deep: bool = False)[source]#
Returns copy of
qibo.quantum_info.clifford.Cliffordobject.- Parameters:
deep (bool, optional) – If
True, creates another copy in memory. Defaults toFalse.- Returns:
copy of original
Cliffordobject.- Return type:
Entanglement measures#
Set of functions to calculate entanglement measures.
Concurrence#
- qibo.quantum_info.concurrence(state, bipartition, check_purity: bool = True, backend=None)[source]#
Calculates concurrence of a pure bipartite quantum state \(\rho \in \mathcal{H}_{A} \otimes \mathcal{H}_{B}\) as
\[C(\rho) = \sqrt{2 \, (\text{tr}^{2}(\rho) - \text{tr}(\rho_{A}^{2}))} \, ,\]where \(\rho_{A} = \text{tr}_{B}(\rho)\) is the reduced density operator obtained by tracing out the qubits in the
bipartition\(B\).- Parameters:
state (ndarray) – statevector or density matrix.
bipartition (list or tuple or ndarray) – qubits in the subsystem to be traced out.
check_purity (bool, optional) – if
True, checks ifstateis pure. IfFalse, it assumesstateis pure . Defaults toTrue.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Concurrence of \(\rho\).
- Return type:
Entanglement of formation#
- qibo.quantum_info.entanglement_of_formation(state, bipartition, base: float = 2, check_purity: bool = True, backend=None)[source]#
Calculates the entanglement of formation \(E_{f}\) of a pure bipartite quantum state \(\rho\), which is given by
\[E_{f} = H([1 - x, x]) \, ,\]where
\[x = \frac{1 + \sqrt{1 - C^{2}(\rho)}}{2} \, ,\]\(C(\rho)\) is the
qibo.quantum_info.concurrence()of \(\rho\), and \(H\) is theqibo.quantum_info.entropies.shannon_entropy().- Parameters:
state (ndarray) – statevector or density matrix.
bipartition (list or tuple or ndarray) – qubits in the subsystem to be traced out.
base (float) – the base of the log in
qibo.quantum_info.entropies.shannon_entropy(). Defaults to \(2\).check_purity (bool, optional) – if
True, checks ifstateis pure. IfFalse, it assumesstateis pure . Default:True.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
entanglement of formation of state \(\rho\).
- Return type:
Negativity#
- qibo.quantum_info.negativity(state, bipartition, backend=None)[source]#
Calculates the negativity of a bipartite quantum state.
Given a bipartite state \(\rho \in \mathcal{H}_{A} \otimes \mathcal{H}_{B}\), the negativity \(\operatorname{Neg}(\rho)\) is given by
\[\operatorname{Neg}(\rho) = \frac{1}{2} \, \left( \norm{\rho_{B}}_{1} - 1 \right) \, ,\]where \(\rho_{B}\) is the reduced density matrix after tracing out qubits in partition \(A\), and \(\norm{\cdot}_{1}\) is the Schatten \(1\)-norm (also known as nuclear norm or trace norm).
- Parameters:
state (ndarray) – statevector or density matrix.
bipartition (list or tuple or ndarray) – qubits in the subsystem to be traced out.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses it uses the current backend. Defaults toNone.
- Returns:
Negativity \(\operatorname{Neg}(\rho)\) of state \(\rho\).
- Return type:
Entanglement fidelity#
- qibo.quantum_info.entanglement_fidelity(channel, nqubits: int, state=None, backend=None)[source]#
Entanglement fidelity \(F_{\mathcal{E}}\) of a
channel\(\mathcal{E}\) onstate\(\rho\) is given by\[F_{\mathcal{E}}(\rho) = F(\rho_{f}, \rho)\]where \(F\) is the
qibo.quantum_info.fidelity()function for states, and \(\rho_{f} = \mathcal{E}_{A} \otimes I_{B}(\rho)\) is the state after the channel \(\mathcal{E}\) was applied to partition \(A\).- Parameters:
channel (
qibo.gates.channels.Channel) – quantum channel acting on partition \(A\).nqubits (int) – total number of qubits in
state.state (ndarray, optional) – statevector or density matrix to be evolved by
channel. IfNone, defaults to the maximally entangled state \(\frac{1}{2^{n}} \, \sum_{k} \, \ket{k}\ket{k}\), where \(n\) isnqubits. Defaults toNone.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Entanglement fidelity \(F_{\mathcal{E}}\).
- Return type:
Meyer-Wallach entanglement#
- qibo.quantum_info.meyer_wallach_entanglement(state, backend=None)[source]#
Compute the Meyer-Wallach entanglement \(Q\) of a
state,\[Q(\rho) = 2\left(1 - \frac{1}{N} \, \sum_{k} \, \text{tr}\left(\rho_{k}^{2}\right)\right) \, ,\]where \(\rho_{k}^{2}\) is the reduced density matrix of qubit \(k\), and \(N\) is the total number of qubits in
state. We use the definition of the Meyer-Wallach entanglement as the average purity proposed in Brennen (2003), which is equivalent to the definition introduced in Meyer and Wallach (2002).- Parameters:
state (ndarray) – statevector or density matrix.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Meyer-Wallach entanglement \(Q\).
- Return type:
References
1. G. K. Brennen, An observable measure of entanglement for pure states of multi-qubit systems, Quantum Information and Computation, vol. 3 (6), 619-626 (2003).
2. D. A. Meyer and N. R. Wallach, Global entanglement in multiparticle systems, J. Math. Phys. 43, 4273–4278 (2002).
Entanglement capability#
- qibo.quantum_info.entangling_capability(circuit, samples: int, seed=None, backend=None)[source]#
Return the entangling capability \(\text{Ent}\) of a parametrized circuit.
It is defined as the average Meyer-Wallach entanglement \(Q\) (
qibo.quantum_info.meyer_wallach_entanglement()) of thecircuit, i.e.\[\text{Ent} = \frac{2}{|\mathcal{S}|}\sum_{\theta_{k} \in \mathcal{S}} \, Q(\rho_{k}) \, ,\]where \(\mathcal{S}\) is the set of sampled circuit parameters, and \(\rho_{k}\) is the state prepared by the circuit with uniformily-sampled parameters \(\theta_{k}\).
Note
Currently, function does not work with
circuitthat contains noisy channels.- Parameters:
circuit (
qibo.models.Circuit) – Parametrized circuit.samples (int) – number of sampled circuit parameter vectors \(|S|\)
seed (int or
numpy.random.Generator, optional) – Either a generator of random numbers or a fixed seed to initialize a generator. IfNone, initializes a generator with a random seed. Default:None.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Entangling capability \(\text{Ent}\).
- Return type:
Entropy measures#
Set of functions to calculate entropy measures.
Shannon entropy#
- qibo.quantum_info.shannon_entropy(prob_dist, base: float = 2, backend=None)[source]#
Calculate the Shannon entropy of a probability array \(\mathbf{p}\), which is given by
\[H(\mathbf{p}) = - \sum_{k = 0}^{d^{2} - 1} \, p_{k} \, \log_{b}(p_{k}) \, ,\]where \(d = \text{dim}(\mathcal{H})\) is the dimension of the Hilbert space \(\mathcal{H}\), \(b\) is the log base (default 2), and \(0 \log_{b}(0) \equiv 0\).
- Parameters:
prob_dist (ndarray or list) – a probability array \(\mathbf{p}\).
base (float) – the base of the log. Defaults to \(2\).
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Shannon entropy \(H(\mathcal{p})\).
- Return type:
Classical relative entropy#
- qibo.quantum_info.classical_relative_entropy(prob_dist_p, prob_dist_q, base: float = 2, backend=None)[source]#
Calculates the relative entropy between two discrete probability distributions.
For probabilities \(\mathbf{p}\) and \(\mathbf{q}\), it is defined as
\[D(\mathbf{p} \, \| \, \mathbf{q}) = \sum_{x} \, \mathbf{p}(x) \, \log\left( \frac{\mathbf{p}(x)}{\mathbf{q}(x)} \right) \, .\]The classical relative entropy is also known as the Kullback-Leibler (KL) divergence.
- Parameters:
prob_dist_p (ndarray or list) – discrete probability distribution \(p\).
prob_dist_q (ndarray or list) – discrete probability distribution \(q\).
base (float) – the base of the log. Defaults to \(2\).
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Classical relative entropy between \(\mathbf{p}\) and \(\mathbf{q}\).
- Return type:
Classical mutual information#
- qibo.quantum_info.classical_mutual_information(prob_dist_joint, prob_dist_p, prob_dist_q, base: float = 2, backend=None)[source]#
Calculates the classical mutual information of two random variables.
Given two random variables \((X, \, Y)\), their mutual information is given by
\[I(X, \, Y) \equiv H(p(x)) + H(q(y)) - H(p(x, \, y)) \, ,\]where \(p(x, \, y)\) is the joint probability distribution of \((X, Y)\), \(p(x)\) is the marginal probability distribution of \(X\), \(q(y)\) is the marginal probability distribution of \(Y\), and \(H(\cdot)\) is the
qibo.quantum_info.entropies.shannon_entropy().- Parameters:
prob_dist_joint (ndarray) – joint probability distribution \(p(x, \, y)\).
prob_dist_p (ndarray) – marginal probability distribution \(p(x)\).
prob_dist_q (ndarray) – marginal probability distribution \(q(y)\).
base (float) – the base of the log. Defaults to \(2\).
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Mutual information \(I(X, \, Y)\).
- Return type:
Classical Rényi entropy#
- qibo.quantum_info.classical_renyi_entropy(prob_dist, alpha: float | int, base: float = 2, backend=None)[source]#
Calculates the classical Rényi entropy \(H_{\alpha}\) of a discrete probability distribution.
For \(\alpha \in (0, \, 1) \cup (1, \, \infty)\) and probability distribution \(\mathbf{p}\), the classical Rényi entropy is defined as
\[H_{\alpha}(\mathbf{p}) = \frac{1}{1 - \alpha} \, \log\left( \sum_{x} \, \mathbf{p}^{\alpha}(x) \right) \, .\]A special case is the limit \(\alpha \to 1\), in which the classical Rényi entropy coincides with the
qibo.quantum_info.entropies.shannon_entropy().Another special case is the limit \(\alpha \to 0\), where the function is reduced to \(\log\left(|\mathbf{p}|\right)\), with \(|\mathbf{p}|\) being the support of \(\mathbf{p}\). This is known as the Hartley entropy (also known as Hartley function or max-entropy).
In the limit \(\alpha \to \infty\), the function reduces to \(-\log(\max_{x}(\mathbf{p}(x)))\), which is called the min-entropy.
- Parameters:
prob_dist (ndarray) – discrete probability distribution.
base (float) – the base of the log. Defaults to \(2\).
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Classical Rényi entropy \(H_{\alpha}\).
- Return type:
Classical Rényi relative entropy#
- qibo.quantum_info.classical_relative_renyi_entropy(prob_dist_p, prob_dist_q, alpha: float | int, base: float = 2, backend=None)[source]#
Calculates the classical relative Rényi entropy between two discrete probability distributions.
This function is also known as Rényi divergence.
For \(\alpha \in (0, \, 1) \cup (1, \, \infty)\) and probability distributions \(\mathbf{p}\) and \(\mathbf{q}\), the classical relative Rényi entropy is defined as
\[H_{\alpha}(\mathbf{p} \, \| \, \mathbf{q}) = \frac{1}{\alpha - 1} \, \log\left( \sum_{x} \, \frac{\mathbf{p}^{\alpha}(x)} {\mathbf{q}^{\alpha - 1}(x)} \right) \, .\]A special case is the limit \(\alpha \to 1\), in which the classical Rényi divergence coincides with the
qibo.quantum_info.entropies.classical_relative_entropy().Another special case is the limit \(\alpha \to 1/2\), where the function is reduced to \(-2 \log\left(\sum_{x} \, \sqrt{\mathbf{p}(x) \, \mathbf{q}(x)} \right)\). The sum inside the \(\log\) is known as the Bhattacharyya coefficient.
In the limit \(\alpha \to \infty\), the function reduces to \(\log(\max_{x}(\mathbf{p}(x) \, \mathbf{q}(x))\).
- Parameters:
prob_dist_p (ndarray or list) – discrete probability distribution \(p\).
prob_dist_q (ndarray or list) – discrete probability distribution \(q\).
base (float) – the base of the log. Defaults to \(2\).
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Classical relative Rényi entropy \(H_{\alpha}(\mathbf{p} \, \| \, \mathbf{q})\).
- Return type:
Classical Tsallis entropy#
- qibo.quantum_info.classical_tsallis_entropy(prob_dist, alpha: float, base: float = 2, backend=None)[source]#
Calculates the classical Tsallis entropy for a discrete probability distribution.
This is defined as
\[S_{\alpha}(\mathbf{p}) = \frac{1}{\alpha - 1} \, \left(1 - \sum_{x} \, \mathbf{p}^{\alpha}(x) \right)\]- Parameters:
prob_dist (ndarray) – discrete probability distribution.
base (float) – the base of the log. Used when
alpha=1.0. Defaults to \(2\).backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Classical Tsallis entropy \(S_{\alpha}(\mathbf{p})\).
- Return type:
Classical Tsallis relative entropy#
- qibo.quantum_info.classical_relative_tsallis_entropy(prob_dist_p, prob_dist_q, alpha: float, base: float = 2, backend=None)[source]#
Calculate the classical relative Tsallis entropy between two discrete probability distributions.
Given a discrete random variable \(\chi\) that has values \(x\) in the set \(\mathcal{X}\) with probability \(\mathrm{p}(x)\) and a discrete random variable \(\upsilon\) that has the values \(x\) in the same set \(\mathcal{X}\) with probability \(\mathrm{q}(x)\), their relative Tsallis entropy is given by
\[D_{\alpha}^{\text{ts}}(\chi \, \| \, \upsilon) = \sum_{x \in \mathcal{X}} \, \mathrm{p}^{\alpha}(x) \, \ln_{\alpha} \left( \frac{\mathrm{p}(x)}{\mathrm{q}(x)} \right) \, ,\]where \(\ln_{\alpha}(x) \equiv \frac{x^{1 - \alpha} - 1}{1 - \alpha}\) is the so-called \(\alpha\)-logarithm. When \(\alpha = 1\), it reduces to
qibo.quantum_info.entropies.classical_relative_entropy.- Parameters:
prob_dist_p (ndarray or list) – discrete probability distribution \(p\).
prob_dist_q (ndarray or list) – discrete probability distribution \(q\).
alpha (float) – entropic index.
base (float) – the base of the log used when \(\alpha = 1\). Defaults to \(2\).
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Tsallis relative entropy \(D_{\alpha}^{\text{ts}}\).
- Return type:
von Neumann entropy#
- qibo.quantum_info.von_neumann_entropy(state, base: float = 2, return_spectrum: bool = False, backend=None)[source]#
Calculate the von-Neumann entropy \(S(\rho)\) of a quantum
state\(\rho\).It is given by
\[S(\rho) = - \text{tr}\left(\rho \, \log(\rho)\right)\]- Parameters:
state (ndarray) – statevector or density matrix.
base (float, optional) – the base of the log. Defaults to \(2\).
return_spectrum – if
True, returnsentropyand \(-\log_{\textup{b}}(\textup{eigenvalues})\), where \(b\) isbase. IfFalse, returns onlyentropy. Default isFalse.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
The von-Neumann entropy \(S\) of
state\(\rho\).- Return type:
Relative von Neumann entropy#
- qibo.quantum_info.relative_von_neumann_entropy(state, target, base: float = 2, backend=None)[source]#
Calculates the relative von Neumann entropy between two quantum states.
Also known as quantum relative entropy, \(S(\rho \, \| \, \sigma)\) is given by
\[S(\rho \, \| \, \sigma) = \text{tr}\left(\rho \, \log(\rho)\right) - \text{tr}\left(\rho \, \log(\sigma)\right)\]where
state\(\rho\) andtarget\(\sigma\) are two quantum states.- Parameters:
state (ndarray) – statevector or density matrix \(\rho\).
target (ndarray) – statevector or density matrix \(\sigma\).
base (float, optional) – the base of the log. Defaults to \(2\).
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Relative von-Neumann entropy \(S(\rho \, \| \, \sigma)\).
- Return type:
Mutual information#
- qibo.quantum_info.mutual_information(state, partition, base: float = 2, backend=None)[source]#
Calculates the mutual information of a bipartite state.
Given a qubit
partition\(A\), the mutual information of state \(\rho\) is given by\[I(\rho) \equiv S(\rho_{A}) + S(\rho_{B}) - S(\rho) \, ,\]where \(B\) is the remaining qubits that are not in partition \(A\), and \(S(\cdot)\) is the
qibo.quantum_info.von_neumann_entropy().- Parameters:
state (ndarray) – statevector or density matrix.
partition (Union[List[int], Tuple[int]]) – indices of qubits in partition \(A\).
base (float, optional) – the base of the log. Defaults to \(2\).
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Mutual information \(I(\rho)\) of
state\(\rho\).- Return type:
Rényi entropy#
- qibo.quantum_info.renyi_entropy(state, alpha: float | int, base: float = 2, backend=None)[source]#
Calculates the Rényi entropy \(H_{\alpha}\) of a quantum state \(\rho\).
For \(\alpha \in (0, \, 1) \cup (1, \, \infty)\), the Rényi entropy is defined as
\[H_{\alpha}(\rho) = \frac{1}{1 - \alpha} \, \log\left( \rho^{\alpha} \right) \, .\]A special case is the limit \(\alpha \to 1\), in which the Rényi entropy coincides with the
qibo.quantum_info.entropies.entropy().Another special case is the limit \(\alpha \to 0\), where the function is reduced to \(\log\left(d\right)\), with \(d = 2^{n}\) being the dimension of the Hilbert space in which
state\(\rho\) lives in. This is known as the Hartley entropy (also known as Hartley function or max-entropy).In the limit \(\alpha \to \infty\), the function reduces to \(-\log(\|\rho\|_{\infty})\), with \(\|\cdot\|_{\infty}\) being the spectral norm. This is known as the min-entropy.
- Parameters:
state (ndarray) – statevector or density matrix.
base (float) – the base of the log. Defaults to \(2\).
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Rényi entropy \(H_{\alpha}\).
- Return type:
Relative Rényi entropy#
- qibo.quantum_info.relative_renyi_entropy(state, target, alpha: float | int, base: float = 2, backend=None)[source]#
Calculates the relative Rényi entropy between two quantum states.
For \(\alpha \in (0, \, 1) \cup (1, \, \infty)\) and quantum states \(\rho\) and \(\sigma\), the relative Rényi entropy is defined as
\[H_{\alpha}(\rho \, \| \, \sigma) = \frac{1}{\alpha - 1} \, \log\left( \textup{tr}\left( \rho^{\alpha} \, \sigma^{1 - \alpha} \right) \right) \, .\]A special case is the limit \(\alpha \to 1\), in which the Rényi entropy coincides with the
qibo.quantum_info.entropies.relative_von_neumann_entropy().In the limit \(\alpha \to \infty\), the function reduces to \(-2 \, \log(\|\sqrt{\rho} \, \sqrt{\sigma}\|_{1})\), with \(\|\cdot\|_{1}\) being the Schatten 1-norm. This is known as the min-relative entropy.
Note
Function raises
NotImplementedErrorwhentarget\(\sigma\) is a pure state and \(\alpha > 1\). This is due to the fact that it is not possible to calculate \(\sigma^{1 - \alpha}\) when \(\alpha > 1\) and \(\sigma\) is a projector, i.e. a singular matrix.- Parameters:
state (ndarray) – statevector or density matrix \(\rho\).
target (ndarray) – statevector or density matrix \(\sigma\).
base (float) – the base of the log. Defaults to \(2\).
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Relative Rényi entropy \(H_{\alpha}(\rho \, \| \, \sigma)\).
- Return type:
Tsallis entropy#
- qibo.quantum_info.tsallis_entropy(state, alpha: float, base: float = 2, backend=None)[source]#
Calculates the Tsallis entropy of a quantum state.
\[S_{\alpha}(\rho) = \frac{1}{1 - \alpha} \, \left( \text{tr}(\rho^{\alpha}) - 1 \right)\]When \(\alpha = 1\), the functions defaults to
qibo.quantum_info.entropies.entropy().- Parameters:
state (ndarray) – statevector or density matrix.
base (float, optional) – the base of the log. Used when
alpha=1.0. Defaults to \(2\).backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Tsallis entropy \(S_{\alpha}(\rho)\).
- Return type:
Relative Tsallis entropy#
- qibo.quantum_info.relative_tsallis_entropy(state, target, alpha: float | int, base: float = 2, backend=None)[source]#
Calculate the relative Tsallis entropy between two quantum states.
For \(\alpha \in [0, \, 2]\) and quantum states \(\rho\) and \(\sigma\), the relative Tsallis entropy is defined as
\[\Delta_{\alpha}^{\text{ts}}(\rho, \, \sigma) = \frac{1 - \text{tr}\left(\rho^{\alpha} \, \sigma^{1 - \alpha}\right)}{1 - \alpha} \, .\]A special case is the limit \(\alpha \to 1\), in which the Tsallis entropy coincides with the
qibo.quantum_info.entropies.relative_von_neumann_entropy().- Parameters:
state (ndarray) – statevector or density matrix \(\rho\).
target (ndarray) – statevector or density matrix \(\sigma\).
alpha (float or int) – entropic index \(\alpha \in [0, \, 2]\).
base (float, optional) – the base of the log used when \(\alpha = 1\). Defaults to \(2\).
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it usesqibo.backends.GlobalBackend. Defaults toNone.
- Returns:
Relative Tsallis entropy \(\Delta_{\alpha}^{\text{ts}}\).
- Return type:
References
1. S. Abe, Nonadditive generalization of the quantum Kullback-Leibler divergence for measuring the degree of purification, Phys. Rev. A 68, 032302.
2. S. Furuichi, K. Yanagi, and K. Kuriyama, Fundamental properties of Tsallis relative entropy, J. Math. Phys., Vol. 45, Issue 12, pp. 4868-4877 (2004) .
Entanglement entropy#
- qibo.quantum_info.entanglement_entropy(state, bipartition, base: float = 2, return_spectrum: bool = False, backend=None)[source]#
Calculates the entanglement entropy \(S\) of bipartition \(A\) of
state\(\rho\). This is given by\[S(\rho_{A}) = -\text{tr}(\rho_{A} \, \log(\rho_{A})) \, ,\]where \(\rho_{A} = \text{tr}_{B}(\rho)\) is the reduced density matrix calculated by tracing out the
bipartition\(B\).- Parameters:
state (ndarray) – statevector or density matrix.
bipartition (list or tuple or ndarray) – qubits in the subsystem to be traced out.
base (float, optional) – the base of the log. Defaults to :math: 2.
return_spectrum – if
True, returnsentropyand eigenvalues ofstate. IfFalse, returns onlyentropy. Default isFalse.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Entanglement entropy \(S\) of
state\(\rho\).- Return type:
Metrics#
Set of functions that are used to calculate metrics of states, (pseudo-)distance measures between states, and distance measures between quantum channels.
Purity#
Impurity#
- qibo.quantum_info.impurity(state, backend=None)[source]#
Impurity of quantum state \(\rho\).
This is given by \(1 - \text{purity}(\rho)\), where \(\text{purity}\) is defined in
qibo.quantum_info.purity().- Parameters:
state (ndarray) – statevector or density matrix.
- Returns:
impurity of
state\(\rho\).- Return type:
Trace distance#
- qibo.quantum_info.trace_distance(state, target, backend=None)[source]#
Trace distance between two quantum states, \(\rho\) and \(\sigma\):
\[T(\rho, \sigma) = \frac{1}{2} \, \|\rho - \sigma\|_{1} = \frac{1}{2} \, \text{tr}\left[ \sqrt{(\rho - \sigma)^{\dagger}(\rho - \sigma)} \right] \, ,\]where \(\|\cdot\|_{1}\) is the Schatten 1-norm.
- Parameters:
state (ndarray) – statevector or density matrix.
target (ndarray) – statevector or density matrix.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Trace distance between
state\(\rho\) andtarget\(\sigma\).- Return type:
Hilbert-Schmidt inner product#
- qibo.quantum_info.hilbert_schmidt_inner_product(operator_A, operator_B, backend=None)[source]#
Calculate the Hilbert-Schmidt inner product between two operators.
Given two operators \(A, \, B \in \mathcal{H}\), the Hilbert-Schmidt inner product between the two is given by
\[\braket{A, \, B}_{\text{HS}} = \text{tr}\left(A^{\dagger} \, B\right) \, .\]- Parameters:
operator_A (ndarray) – operator \(A\).
operator_B (ndarray) – operator \(B\).
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Hilbert-Schmidt inner product \(\braket{A, \, B}_{\text{HS}}\).
- Return type:
Hilbert-Schmidt distance#
- qibo.quantum_info.hilbert_schmidt_distance(state, target, backend=None)[source]#
Calculate the Hilbert-Schmidt distance between two quantum states:
\[\braket{\rho - \sigma, \, \rho - \sigma}_{\text{HS}} = \text{tr}\left((\rho - \sigma)^{2}\right) \, ,\]where \(\braket{\cdot, \, \cdot}_{\text{HS}}\) is the
qibo.quantum_info.hilbert_schmidt_inner_product().- Parameters:
state (ndarray) – statevector or density matrix.
target (ndarray) – statevector or density matrix.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Hilbert-Schmidt distance between
state\(\rho\) andtarget\(\sigma\).- Return type:
References
1. P. J. Coles, M. Cerezo, and L. Cincio, Strong bound between trace distance and Hilbert-Schmidt distance for low-rank states, Phys. Rev. A 100, 022103 (2019).
Fidelity#
- qibo.quantum_info.fidelity(state, target, backend=None)[source]#
Fidelity \(F(\rho, \sigma)\) between
state\(\rho\) andtargetstate \(\sigma\). In general,\[F(\rho, \sigma) = \text{tr}^{2}\left( \sqrt{\sqrt{\sigma} \, \rho^{\dagger} \, \sqrt{\sigma}} \right) \, .\]However, when at least one of the states is pure, then
\[F(\rho, \sigma) = \text{tr}(\rho \, \sigma)\]- Parameters:
state (ndarray) – statevector or density matrix.
target (ndarray) – statevector or density matrix.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Fidelity between
state\(\rho\) andtarget\(\sigma\).- Return type:
Infidelity#
- qibo.quantum_info.infidelity(state, target, backend=None)[source]#
Infidelity between
state\(\rho\) andtargetstate \(\sigma\), which is given by\[1 - F(\rho, \, \sigma) \, ,\]where \(F(\rho, \, \sigma)\) is the
qibo.quantum_info.fidelity()betweenstateandtarget.- Parameters:
state (ndarray) – statevector or density matrix.
target (ndarray) – statevector or density matrix.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Infidelity between
state\(\rho\) andtarget\(\sigma\).- Return type:
A fidelity#
- qibo.quantum_info.a_fidelity(state, target, backend=None)[source]#
Return the \(A\)-fidelity between two quantum states.
For a quantum
state\(\rho\) and atargetquantum state \(\sigma\), the \(A\)-fidelity is defined as:\[F_{\text{A}}(\rho, \, \sigma) = \text{tr}^{2}(\sqrt{\rho} \, \sqrt{\sigma}) \, .\]- Parameters:
state (ndarray) – statevector or density matrix.
target (ndarray) – statevector or density matrix.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
\(A\)-fidelity between \(\rho\) and \(\sigma\).
- Return type:
References
1. Y.-C. Liang, Y.-H. Yeh, P. E. M. F. Mendonça, R. Y. Teh, M. D. Reid, and P. D. Drummond, Quantum fidelity measures for mixed states, Rep. Prog. Phys. 82 076001 (2019).
2. Z. Ma, F.-L. Zhang, and J.-L. Chen. Geometric interpretation for the A fidelity and its relation with the Bures fidelity, Phys. Rev. A, 78(6):064305, (2008).
N fidelity#
- qibo.quantum_info.n_fidelity(state, target, backend=None)[source]#
Return the \(N\)-fidelity between two quantum states.
For a quantum
state\(\rho\) and atargetquantum state \(\sigma\), the \(N\)-fidelity is defined as:\[F_{\text{N}}(\rho, \, \sigma) = \text{tr}(\rho \, \sigma) + \sqrt{1 - \text{tr}(\rho^{2})} \, \sqrt{1 - \text{tr}(\rho^{2})} \, ,\]where \(\text{tr}(\varrho^{2})\) is the
qibo.quantum_info.purityof a quantum state \(\varrho\).- Parameters:
state (ndarray) – statevector or density matrix.
target (ndarray) – statevector or density matrix.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
\(N\)-fidelity between \(\rho\) and \(\sigma\).
- Return type:
References
1. Y.-C. Liang, Y.-H. Yeh, P. E. M. F. Mendonça, R. Y. Teh, M. D. Reid, and P. D. Drummond, Quantum fidelity measures for mixed states, Rep. Prog. Phys. 82 076001 (2019).
2. P. E. M. F. Mendonça, R. d. J. Napolitano, M. A. Marchiolli, C. J. Foster, and Y.-C. Liang. Alternative fidelity measure between quantum states, Phys. Rev. A, 78 052330 (2008).
3. A. Miszczak, Z. Puchala, P. Horodecki, A. Uhlmann, and K. Zyczkowski. Sub- and super-fidelity as bounds for quantum fidelity. Quantum Inf. Comput., 9(1):103–130, (2009).
Chen fidelity#
- qibo.quantum_info.chen_fidelity(state, target, backend=None)[source]#
Return the Chen fidelity between two quantum states.
For a quantum
state\(\rho\) and atargetquantum state \(\sigma\), the Chen fidelity is defined as:\[F_{\text{C}}(\rho, \, \sigma) = \frac{1 - r}{2} + \frac{1 + r}{2} \, F_{\text{N}}(\rho, \, \sigma) \, ,\]where \(\text{tr}(\varrho^{2})\) is the
qibo.quantum_info.purityof a quantum state \(\varrho\).- Parameters:
state (ndarray) – statevector or density matrix.
target (ndarray) – statevector or density matrix.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Chen fidelity between \(\rho\) and \(\sigma\).
- Return type:
References
1. Y.-C. Liang, Y.-H. Yeh, P. E. M. F. Mendonça, R. Y. Teh, M. D. Reid, and P. D. Drummond, Quantum fidelity measures for mixed states, Rep. Prog. Phys. 82 076001 (2019).
2. J.-L. Chen, L. Fu, A. A. Ungar, and X.-G. Zhao, Alternative fidelity measure between two states of an N-state quantum system, Phys. Rev. A 65, 054304 (2002).
Geometric-mean fidelity#
- qibo.quantum_info.geometric_mean_fidelity(state, target, backend=None)[source]#
Return the geometric-mean fidelity between two quantum states.
For a quantum
state\(\rho\) and atargetquantum state \(\sigma\), the geometric-mean fidelity is defined as:\[F_{\text{GM}}(\rho, \, \sigma) = \frac{\text{tr}(\rho \, \sigma)} {\sqrt{\text{tr}(\rho^{2}) \, \text{tr}(\sigma^{2})}} \, ,\]where \(\text{tr}(\varrho^{2})\) is the
qibo.quantum_info.purityof a quantum state \(\varrho\). If at least one of the quantum states is pure, then the geometric-mean fidelity reduces to the usualqibo.quantum_info.fidelity.- Parameters:
state (ndarray) – statevector or density matrix.
target (ndarray) – statevector or density matrix.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Geometric-mean fidelity between \(\rho\) and \(\sigma\).
- Return type:
References
1. Y.-C. Liang, Y.-H. Yeh, P. E. M. F. Mendonça, R. Y. Teh, M. D. Reid, and P. D. Drummond, Quantum fidelity measures for mixed states, Rep. Prog. Phys. 82 076001 (2019).
2. X. Wang, C.-S. Yu, and X.X. Yi. An alternative quantum fidelity for mixed states of qudits. Phys. Lett. A, 373(1):58–60, (2008).
Max fidelity#
- qibo.quantum_info.max_fidelity(state, target, backend=None)[source]#
Return max fidelity between two quantum states.
For a quantum
state\(\rho\) and atargetquantum state \(\sigma\), the max fidelity is defined as:\[F_{\text{max}}(\rho, \, \sigma) = \frac{\text{tr}(\rho \, \sigma)} {\text{max}(\text{tr}(\rho^{2}), \, \text{tr}(\sigma^{2}))} \, ,\]where \(\text{tr}(\varrho^{2})\) is the
qibo.quantum_info.purityof a quantum state \(\varrho\). If at least one of the quantum states is pure, then the max fidelity reduces to the usualqibo.quantum_info.fidelity.- Parameters:
state (ndarray) – statevector or density matrix.
target (ndarray) – statevector or density matrix.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Max fidelity between \(\rho\) and \(\sigma\).
- Return type:
References
1. Y.-C. Liang, Y.-H. Yeh, P. E. M. F. Mendonça, R. Y. Teh, M. D. Reid, and P. D. Drummond, Quantum fidelity measures for mixed states, Rep. Prog. Phys. 82 076001 (2019).
Bures angle#
- qibo.quantum_info.bures_angle(state, target, backend=None)[source]#
Calculates the Bures angle \(D_{A}\) between a
state\(\rho\) and atargetstate \(\sigma\). This is given by\[D_{A}(\rho, \, \sigma) = \text{arccos}\left(\sqrt{F(\rho, \, \sigma)}\right) \, ,\]where \(F(\rho, \sigma)\) is the
qibo.quantum_info.fidelity()between state and target.- Parameters:
state (ndarray) – statevector or density matrix.
target (ndarray) – statevector or density matrix.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Bures angle between
stateandtarget.- Return type:
Bures distance#
- qibo.quantum_info.bures_distance(state, target, backend=None)[source]#
Calculates the Bures distance \(D_{B}\) between a
state\(\rho\) and atargetstate \(\sigma\). This is given by\[D_{B}(\rho, \, \sigma) = \sqrt{2 \, \left(1 - \sqrt{F(\rho, \, \sigma)}\right)}\]where \(F(\rho, \sigma)\) is the
qibo.quantum_info.fidelity()between state and target.- Parameters:
state (ndarray) – statevector or density matrix.
target (ndarray) – statevector or density matrix.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Bures distance between
stateandtarget.- Return type:
Process fidelity#
- qibo.quantum_info.process_fidelity(channel, target=None, check_unitary: bool = False, backend=None)[source]#
Process fidelity between a quantum
channel\(\mathcal{E}\) and atargetunitary channel \(U\). The process fidelity is defined as\[F_{\text{pro}}(\mathcal{E}, \mathcal{U}) = \frac{1}{d^{2}} \, \text{tr}(\mathcal{E}^{\dagger} \, \mathcal{U})\]- Parameters:
channel – quantum channel \(\mathcal{E}\).
target (optional) – quantum channel \(U\). If
None, target is the Identity channel. Defaults toNone.check_unitary (bool, optional) – if
True, checks if one of the input channels is unitary. Default:False.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Process fidelity between
channelandtarget.- Return type:
Process infidelity#
- qibo.quantum_info.process_infidelity(channel, target=None, check_unitary: bool = False, backend=None)[source]#
Process infidelity between quantum channel \(\mathcal{E}\) and a
targetunitary channel \(U\). The process infidelity is defined as\[1 - F_{\text{pro}}(\mathcal{E}, \mathcal{U}) \, ,\]where \(F_{\text{pro}}\) is the
qibo.quantum_info.process_fidelity().- Parameters:
channel – quantum channel \(\mathcal{E}\).
target (optional) – quantum channel \(U\). If
None, target is the Identity channel. Defaults toNone.check_unitary (bool, optional) – if
True, checks if one of the input channels is unitary. Defaults toFalse.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Process infidelity between
channel\(\mathcal{E}\) andtarget\(U\).- Return type:
Average gate fidelity#
- qibo.quantum_info.average_gate_fidelity(channel, target=None, check_unitary: bool = False, backend=None)[source]#
Average gate fidelity between a quantum
channel\(\mathcal{E}\) and atargetunitary channel \(U\). The average gate fidelity is defined as\[F_{\text{avg}}(\mathcal{E}, \mathcal{U}) = \frac{d \, F_{pro}(\mathcal{E}, \mathcal{U}) + 1}{d + 1}\]where \(d\) is the dimension of the channels and \(F_{pro}(\mathcal{E}, \mathcal{U})\) is the
process_fidelily()of channel \(\mathcal{E}\) with respect to the unitary channel \(\mathcal{U}\).- Parameters:
channel – quantum channel \(\mathcal{E}\).
target (optional) – quantum channel \(\mathcal{U}\). If
None, target is the Identity channel. Defaults toNone.check_unitary (bool, optional) – if
True, checks if one of the input channels is unitary. Default:False.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Process fidelity between channel \(\mathcal{E}\) and target unitary channel \(\mathcal{U}\).
- Return type:
Gate error#
- qibo.quantum_info.gate_error(channel, target=None, check_unitary: bool = False, backend=None)[source]#
Gate error between a quantum
channel\(\mathcal{E}\) and atargetunitary channel \(U\), which is defined as\[E(\mathcal{E}, \mathcal{U}) = 1 - F_{\text{avg}}(\mathcal{E}, \mathcal{U}) \, ,\]where \(F_{\text{avg}}(\mathcal{E}, \mathcal{U})\) is the
qibo.quantum_info.average_gate_fidelity().- Parameters:
channel – quantum channel \(\mathcal{E}\).
target (optional) – quantum channel \(\mathcal{U}\). If
None, target is the Identity channel. Defaults toNone.check_unitary (bool, optional) – if
True, checks if one of the input channels is unitary. Default:False.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Gate error between
channel\(\mathcal{E}\) andtarget\(\mathcal{U}\).- Return type:
Diamond Norm#
- qibo.quantum_info.diamond_norm(channel, target=None, backend=None, **kwargs)[source]#
Calculates the diamond norm \(\|\mathcal{E}\|_{\diamond}\) of
channel\(\mathcal{E}\), which is given by\[\|\mathcal{E}\|_{\diamond} = \max_{\rho} \, \| \left(\mathcal{E} \otimes I_{d^{2}}\right)(\rho) \|_{1} \, ,\]where \(I_{d^{2}}\) is the \(d^{2} \times d^{2}\) Identity operator, \(d = 2^{n}\), \(n\) is the number of qubits, and \(\|\cdot\|_{1}\) denotes the trace norm.
If a
targetchannel \(\Lambda\) is specified, then it calculates \(\| \mathcal{E} - \Lambda\|_{\diamond}\).Example:
from qibo.quantum_info import diamond_norm, random_unitary, to_choi nqubits = 1 dim = 2**nqubits unitary = random_unitary(dim) unitary = to_choi(unitary, order="row") unitary_2 = random_unitary(dim) unitary_2 = to_choi(unitary_2, order="row") dnorm = diamond_norm(unitary, unitary_2)
- Parameters:
channel (ndarray) – row-vectorized Choi representation of a quantum channel.
target (ndarray, optional) – row-vectorized Choi representation of a target quantum channel. Defaults to
None.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.kwargs – optional arguments to pass to CVXPY solver. For more information, please visit CVXPY’s API documentation.
- Returns:
diamond norm of either
channelorchannel - target.- Return type:
Note
This function requires the optional CVXPY package to be installed.
Expressibility of parameterized quantum circuits#
- qibo.quantum_info.expressibility(circuit, power_t: int, samples: int, order: int | float | str | None = 2, backend=None)[source]#
Returns the expressibility \(\|A\|\) of a parametrized circuit, where
\[A = \int_{\text{Haar}} d\psi \, \left(|\psi\rangle\right.\left. \langle\psi|\right)^{\otimes t} - \int_{\Theta} d\psi \, \left(|\psi_{\theta}\rangle\right.\left. \langle\psi_{\theta}|\right)^{\otimes t}\]- Parameters:
circuit (
qibo.models.Circuit) – Parametrized circuit.power_t (int) – power that defines the \(t\)-design.
samples (int) – number of samples to estimate the integrals.
order (int or float or str, optional) – order of the norm \(\|A\|\). For specifications, see
qibo.backends.abstract.calculate_norm(). Defaults to \(2\).backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Expressibility of parametrized circuit.
- Return type:
Frame Potential#
- qibo.quantum_info.frame_potential(circuit, power_t: int, samples: int = None, backend=None)[source]#
Returns the frame potential of a parametrized circuit under uniform sampling of the parameters.
For \(n\) qubits and moment \(t\), the frame potential \(\mathcal{F}_{\mathcal{U}}^{(t)}\) if given by [1]
\[\mathcal{F}_{\mathcal{U}}^{(t)} = \int_{U,V \in \mathcal{U}} \, \text{d}U \, \text{d}V \, \bigl| \, \text{tr}(U^{\dagger} \, V) \, \bigr|^{2t} \, ,\]where \(\mathcal{U}\) is the group of unitaries defined by the parametrized circuit. The frame potential is approximated by the average
\[\mathcal{F}_{\mathcal{U}}^{(t)} \approx \frac{1}{N} \, \sum_{k=1}^{N} \, \bigl| \, \text{tr}(U_{k}^{\dagger} \, V_{k}) \, \bigr|^{2t} \, ,\]where \(N\) is the number of
samples.- Parameters:
circuit (
qibo.models.circuit.Circuit) – Parametrized circuit.power_t (int) – power that defines the \(t\)-design.
samples (int) – number of samples to estimate the integral.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Frame potential of the parametrized circuit.
- Return type:
References
1. M. Liu et al., Estimating the randomness of quantum circuit ensembles up to 50 qubits. arXiv:2205.09900 [quant-ph].
Quantum Fisher Information Matrix#
- qibo.quantum_info.quantum_fisher_information_matrix(circuit, parameters=None, initial_state=None, return_complex: bool = True, backend=None)[source]#
Calculate the Quantum Fisher Information Matrix (QFIM) of a parametrized
circuit.Given a set of
parameters\(\theta = \{\theta_{k}\}_{k\in[M]}\) and a parameterized unitarycircuit\(U(\theta)\) acting on aninitial_state\(\ket{\phi}\), the QFIM is such that its elements can be calculated as\[\mathbf{F}_{jk} = 4 \, \text{Re}\left\{ \braket{\partial_{j} \psi | \partial_{k} \psi} - \braket{\partial_{j} \psi | \psi}\!\braket{\psi | \partial_{k} \psi} \right\} \, ,\]where we have used the short notations \(\ket{\psi} \equiv \ket{\psi(\theta)} = U(\theta) \ket{\phi}\), and \(\ket{\partial_{k} \psi} \equiv \frac{\partial} {\partial\theta_{k}} \ket{\psi(\theta)}\). If the
initial_state\(\ket{\phi}\) is not specified, it defaults to \(\ket{0}^{\otimes n}\).- Parameters:
circuit (
qibo.models.circuit.Circuit) – parametrized circuit \(U(\theta)\).parameters (ndarray, optional) – parameters whose QFIM to calculate. If
None, QFIM is calculated with the paremeters fromcircuit, i.e.parameters = circuit.get_parameters(). Defaults toNone.initial_state (ndarray, optional) – Initial configuration. It can be specified by the setting the state vector using an array or a circuit. If
None, the initial state is \(\ket{0}^{\otimes n}\). Defaults toNone.return_complex (bool, optional) – If
True, calculates the Jacobian matrix of real and imaginary parts of \(\ket{\psi(\theta)}\). IfFalse, calculates only the Jacobian matrix of the real part. Defaults toTrue.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it usesqibo.backends.GlobalBackend. Defaults toNone.
- Returns:
Quantum Fisher Information \(\mathbf{F}\).
- Return type:
ndarray
Linear Algebra Operations#
Collection of linear algebra operations that are commonly used in quantum information theory.
Commutator#
- qibo.quantum_info.commutator(operator_1, operator_2)[source]#
Returns the commutator of
operator_1andoperator_2.The commutator of two matrices \(A\) and \(B\) is given by
\[[A, B] = A \, B - B \, A \,.\]- Parameters:
operator_1 (ndarray) – First operator.
operator_2 (ndarray) – Second operator.
- Returns:
Commutator of
operator_1andoperator_2.- Return type:
ndarray
Anticommutator#
- qibo.quantum_info.anticommutator(operator_1, operator_2)[source]#
Returns the anticommutator of
operator_1andoperator_2.The anticommutator of two matrices \(A\) and \(B\) is given by
\[\{A, B\} = A \, B + B \, A \,.\]- Parameters:
operator_1 (ndarray) – First operator.
operator_2 (ndarray) – Second operator.
- Returns:
Anticommutator of
operator_1andoperator_2.- Return type:
ndarray
Partial trace#
- qibo.quantum_info.partial_trace(state, traced_qubits: List[int] | Tuple[int, ...], backend=None)[source]#
Returns the density matrix resulting from tracing out
traced_qubitsfromstate.Total number of qubits is inferred by the shape of
state.- Parameters:
state (ndarray) – density matrix or statevector.
traced_qubits (Union[List[int], Tuple[int]]) – indices of qubits to be traced out.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Density matrix of the remaining qubit(s).
- Return type:
ndarray
Partial transpose#
- qibo.quantum_info.partial_transpose(operator, partition: List[int] | Tuple[int, ...], backend=None)[source]#
Return matrix after the partial transposition of
partitionqubits inoperator.Given a \(n\)-qubit operator \(O \in \mathcal{H}_{A} \otimes \mathcal{H}_{B}\), the partial transpose with respect to
partition\(B\) is given by\[\begin{split}\begin{align} O^{T_{B}} &= \sum_{jklm} \, O_{lm}^{jk} \, \ketbra{j}{k} \otimes \left(\ketbra{l}{m}\right)^{T} \\ &= \sum_{jklm} \, O_{lm}^{jk} \, \ketbra{j}{k} \otimes \ketbra{m}{l} \\ &= \sum_{jklm} \, O_{ml}^{jk} \, \ketbra{j}{k} \otimes \ketbra{l}{m} \, , \end{align}\end{split}\]where the superscript \(T\) indicates the transposition operation, and \(T_{B}\) indicates transposition on
partition\(B\). The total number of qubits is inferred by the shape ofoperator.- Parameters:
operator (ndarray) – \(1\)- or \(2\)-dimensional operator, or an array of \(1\)- or \(2\)-dimensional operators,
partition (Union[List[int], Tuple[int, ...]]) – indices of qubits to be transposed.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses it uses the current backend. Defaults toNone.
- Returns:
Partially transposed operator(s) \(\O^{T_{B}}\).
- Return type:
ndarray
Matrix exponentiation#
- qibo.quantum_info.matrix_exponentiation(matrix, phase: float | int | complex | None = None, eigenvectors=None, eigenvalues=None, backend=None)[source]#
Calculates the exponential of a matrix.
Given a
matrix\(H\) and aphase\(\theta\), it returns the exponential of the form\[\exp\left(\theta \, H \right) \, .\]If the
eigenvectorsandeigenvaluesare given, the matrix diagonalization is used for the exponentiation.- Parameters:
matrix (ndarray) – matrix to be exponentiated.
phase (float or int or complex) – phase that multiplies the matrix. If
None, defaults to \(1\). Defaults toNone.eigenvectors (ndarray, optional) – _if not
None, eigenvectors are used to calculatematrixexponentiation as part of diagonalization. Must be used together witheigenvalues. Defaults toNone.eigenvalues (ndarray, optional) – if not
None, eigenvalues are used to calculatematrixexponentiation as part of diagonalization. Must be used together witheigenvectors. Defaults toNone.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
matrix exponential of \(-i \, \theta \, H\).
- Return type:
ndarray
Matrix logarithm#
- qibo.quantum_info.matrix_logarithm(matrix, base: float | int = 2, eigenvectors=None, eigenvalues=None, backend=None)[source]#
Calculates the logarithm of a matrix.
Given a
matrix\(A\) and a log base \(b\), it returns the logarithm of the form\[\log_{b}\left(\theta \, H \right) \, .\]If the
eigenvectorsandeigenvaluesare given, the matrix diagonalization is used for the calculation.- Parameters:
matrix (ndarray) – matrix to be logarithmed.
eigenvectors (ndarray, optional) – _if not
None, eigenvectors are used to calculate thematrixlogarithm as part of diagonalization. Must be used together witheigenvalues. Defaults toNone.eigenvalues (ndarray, optional) – if not
None, eigenvalues are used to calculate thematrixlogarithm as part of diagonalization. Must be used together witheigenvectors. Defaults toNone.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Matrix logarithm \(\log_{b}(H)\).
- Return type:
ndarray
Matrix power#
- qibo.quantum_info.matrix_power(matrix, power: float | int, precision_singularity: float = 1e-14, backend=None)[source]#
Given a
matrix\(A\) and power \(\alpha\), calculate \(A^{\alpha}\).- Parameters:
matrix (ndarray) – matrix whose power to calculate.
precision_singularity (float, optional) – If determinant of
matrixis smaller thanprecision_singularity, then matrix is considered to be singular. Used whenpoweris negative.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
matrix power \(A^{\alpha}\).
- Return type:
ndarray
Matrix square root#
- qibo.quantum_info.matrix_sqrt(matrix, backend=None)[source]#
Given a
matrix\(A\), calculate \(A^{1/2}\).- Parameters:
matrix (ndarray) – matrix whose power to calculate.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Matrix power \(A^{1/2}\).
- Return type:
ndarray
Singular value decomposition#
- qibo.quantum_info.singular_value_decomposition(matrix, backend=None)[source]#
Calculate the Singular Value Decomposition (SVD) of
matrix.Given an \(M \times N\) complex matrix \(A\), its SVD is given by
where \(U\) and \(V\) are, respectively, an \(M \times M\) and an \(N \times N\) complex unitary matrices, and \(S\) is an \(M \times N\) diagonal matrix with the singular values of \(A\).
- Parameters:
matrix (ndarray) – matrix whose SVD to calculate.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Singular value decomposition of \(A\), i.e. \(U\), \(S\), and \(V^{\dagger}\), in that order.
- Return type:
ndarray, ndarray, ndarray
Schmidt decomposition#
- qibo.quantum_info.schmidt_decomposition(state, partition: List[int] | Tuple[int, ...], backend=None)[source]#
Return the Schmidt decomposition of a \(n\)-qubit bipartite pure quantum
state.Given a bipartite pure state \(\ket{\psi}\in\mathcal{H}_{A}\otimes\mathcal{H}_{B}\), its Schmidt decomposition is given by
\[\ket{\psi} = \sum_{k = 1}^{\min\{a, \, b\}} \, c_{k} \, \ket{\phi_{k}} \otimes \ket{\nu_{k}} \, ,\]with \(a\) and \(b\) being the respective cardinalities of \(\mathcal{H}_{A}\) and \(\mathcal{H}_{B}\), and \(\{\phi_{k}\}_{k\in[\min\{a, \, b\}]} \subset \mathcal{H}_{A}\) and \(\{\nu_{k}\}_{k\in[\min\{a, \, b\}]} \subset \mathcal{H}_{B}\) being orthonormal sets. The coefficients \(\{c_{k}\}_{k\in[\min\{a, \, b\}]}\) are real, non-negative, and unique up to re-ordering.
The decomposition is calculated using
qibo.quantum_info.singular_value_decomposition(), resulting in\[\ketbra{\psi}{\psi} = U \, S \, V^{\dagger} \, ,\]where \(U\) is an \(a \times a\) unitary matrix, \(V\) is an \(b \times b\) unitary matrix, and \(S\) is an \(a \times b\) positive semidefinite diagonal matrix that contains the singular values of \(\ketbra{\psi}{\psi}\).
- Parameters:
state (ndarray) – stevector or density matrix.
partition (Union[List[int], Tuple[int, ...]]) – indices of qubits in one of the two partitions. The other partition is inferred as the remaining qubits.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it usesqibo.backends.GlobalBackend. Defaults toNone.
- Returns:
Respectively, the matrices \(U\), \(S\), and \(V^{\dagger}\).
- Return type:
ndarray, ndarray, ndarray
Lanczos algorithm#
- qibo.quantum_info.lanczos(matrix, steps: int = None, initial_vector=None, precision_tol: float = 1e-08, seed=None, backend=None)[source]#
Lanczos iterative method to tridiagonalize a Hermitian matrix.
Given a \(N \times N\) Hermitian matrix \(H\) and a number of iterations \(m \leq N\), the Lanczos algorithm outputs a \(N \times m\) orthonormal matrix \(U\) and a \(m \times m\) tridiagonal real symmetric matrix \(T = U^{\dagger} \, H \, U\). If \(m = N\), then \(U\) is an unitary matrix. The eigenvalues of \(T\) and \(H\) coincide, while \(U \ket{\mathbf{x}}\) are the eigenvectors of \(H\), with \(\ket{\mathbf{x}}\) being the eigenvectors of \(T\).
This reduces the problem of diagonalization of \(H\) to constructing the matrix \(U\) and diagonalizing \(T\).
With \(\|\cdot\|_{2}\) being the Euclidean norm, the algorithm goes as follows:
Generate random \(\ket{v_{1}} \in \mathbb{C}^{N}\) such that \(\|\ket{v_{1}}\|_{2} = 1\)
\(\ket{\omega_{1}^{\prime}} = H \ket{v_{1}}\)
\(\alpha_{1} = \braket{\omega_{1}^{\prime} | v_{1}}\)
\(\ket{\omega_{1}} = H \ket{v_{1}} - \alpha_{1} \ket{v_{1}}\)
- For \(j = 2, \dots, m - 1\):
\(\beta_{j} = \|\omega_{j-1}\|_{2}\)
\(\ket{v_{j}} = \ket{\omega_{j-1}} \, / \, \beta_{j}\) If \(\beta_{j} \neq 0\) else generate random \(\ket{v_{j}}\) such that \(\ket{v_{j}} \perp \{\ket{v_{j^{\prime}}}\}_{j^{\prime} \in [1, j-1]}\)
\(\ket{\omega_{j}^{\prime}} = H \ket{v_{j}}\)
\(\alpha_{j} = \braket{\omega_{j}^{\prime} | v_{j}}\)
\(\ket{\omega_{j}} = \ket{\omega_{j}^{\prime}} - \alpha_{j} \ket{v_{j}} - \beta_{j} \ket{v_{j-1}}\)
The columns of the orthogonal matrix \(U\) are the Lanczos vectors \(\{\ket{v_{j}}\}_{j\in[1, m]}\).
- Parameters:
matrix (ndarray) – square Hermitian matrix to be tridiagonalized.
steps (int, optional) – number of iterations \(m\). If
None, defaults to the size ofmatrix. Defaults toNone.initial_vector (ndarray, optional) – vector to be used as the initial Lanczos vector \(\ket{v_{1}}\). If
None, array is uniformly sampled. Defaults toNone.precision_tol (float, optional) – precision threshold such that for \(\beta_{j}\) smaller than
precision_tol, it is considered to be zero.seed (int or
numpy.random.Generator, optional) – Seed for the initial random vector \(\ket{v_{1}}\) Either a generator of random numbers or a fixed seed to initialize a generator. IfNone, initializes a generator with a random seed. Defaults toNone.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Tridiagonal matrix and the orthogonal matrix of Lanczos vectors, respectively.
- Return type:
(ndarray, ndarray)
References
1. Lanczos, C. An iteration method for the solution of the eigenvalue problem of linear differential and integral operators, Journal of Research of the National Bureau of Standards. 45 (4): 255–282 (1950).
Quantum Networks#
Quantum network is an object that unifies the representation of quantum states, channels, observables, and higher-order quantum operators.
For more details, see G. Chiribella et al., Theoretical framework for quantum networks, Physical Review A 80.2 (2009): 022339.
- class qibo.quantum_info.quantum_networks.QuantumNetwork(tensor, partition: List[int] | Tuple[int] | None = None, system_input: List[bool] | Tuple[bool] | None = None, pure: bool = False, backend=None)[source]#
This class stores the representation of the quantum network as a tensor. This is a unique representation of the quantum network.
A minimum quantum network is a quantum channel, which is a quantum network of the form \(J[n \to m]\), where \(n\) is the dimension of the input system , and \(m\) is the dimension of the output system. A quantum state is a quantum network of the form \(J: 1 \to n\), such that the input system is trivial. An observable is a quantum network of the form \(J: n \to 1\), such that the output system is trivial.
A quantum network may contain multiple input and output systems. For example, a “quantum comb” is a quantum network of the form \(J: n', n \to m, m'\), which convert a quantum channel of the form \(J: n \to m\) to a quantum channel of the form \(J: n' \to m'\).
- Parameters:
tensor (ndarray) – input Choi operator.
system_input (List[bool] or Tuple[bool], optional) – mask on the output system of the Choi operator. If
None, defaults to(True,False,True,False,...), wherelen(system_input)=len(partition). Defaults toNone.pure (bool, optional) –
Truewhentensoris a “pure” representation (e.g. a pure state, a unitary operator, etc.),Falseotherwise. Defaults toFalse.backend (
qibo.backends.abstract.Backend, optional) – Backend to be used in calculations. IfNone, defaults to the current backend. Defaults toNone.
- classmethod from_operator(operator, partition: List[int] | Tuple[int] | None = None, system_input: List[bool] | Tuple[bool] | None = None, pure: bool = False, backend=None)[source]#
Construct a
qibo.quantum_info.QuantumNetworkobject from a ndarray.This method converts a Choi operator to the internal representation of
qibo.quantum_info.quantum_networks.QuantumNetwork. The input array can be a pure state, a Choi operator, a unitary operator, etc.- Parameters:
arr (ndarray) – input numpy array.
partition (List[int] or Tuple[int], optional) – partition of
arr. IfNone, defaults to the shape ofarr. Defaults toNone.system_input (List[bool] or Tuple[bool], optional) – mask on the input system of the Choi operator. If
None, defaults to(True,False,True,False...), wherelen(system_input)=len(partition). Defaults toNone.pure (bool, optional) –
Truewhenarris a “pure” representation (e.g. a pure state, a unitary operator, etc.),Falseotherwise. Defaults toFalse.backend (
qibo.backends.abstract.Backend, optional) – Backend to be used in calculations. IfNone, defaults to the current backend. Defaults toNone.
- Returns:
quantum network constructed from the input Choi operator.
- Return type:
- operator(full: bool = False, backend=None)[source]#
Returns the Choi operator of the quantum network.
The shape of the returned operator is \((*self.partition, *self.partition)\).
- Parameters:
full (bool, optional) – If this is
False, and the network is pure, the method will only return the eigenvector (unique when the network is pure). IfTrue, returns the full tensor of the quantum network. Defaults toFalse.backend (
qibo.backends.abstract.Backend, optional) – Backend to be used to return the Choi operator. IfNone, defaults to the backend defined when initializing theqibo.quantum_info.quantum_networks.QuantumNetworkobject. Defaults toNone.
- Returns:
Choi operator of the quantum network.
- Return type:
ndarray
- matrix(backend=None)[source]#
Returns the Choi operator of the quantum network in the matrix form. The shape of the returned operator is \((self.dims, self.dims)\).
- Parameters:
backend (
qibo.backends.abstract.Backend, optional) – Backend to be used to return the Choi operator. IfNone, defaults to the backend defined when initializing theqibo.quantum_info.quantum_networks.QuantumNetworkobject. Defaults toNone.- Returns:
Choi operator of the quantum network.
- Return type:
ndarray
- is_hermitian(order: int | str | None = None, precision_tol: float = 1e-08)[source]#
Returns bool indicating if the Choi operator \(\mathcal{J}\) is Hermitian.
Hermicity is calculated as distance between \(\mathcal{J}\) and \(\mathcal{J}^{\dagger}\) with respect to a given norm. Default is the
Hilbert-Schmidtnorm (also known asFrobeniusnorm).For specifications on the other possible values of the parameter
orderfor thetensorflowbackend, please refer to tensorflow.norm. For all other backends, please refer to numpy.linalg.norm.- Parameters:
- Returns:
- Hermiticity condition. If the adjoint of the Choi operator is equal to the
Choi operator, the method returns
True. If the input is pure, the its always Hermitian.
- Return type:
- is_positive_semidefinite(precision_tol: float = 1e-08)[source]#
Returns bool indicating if Choi operator \(\mathcal{J}\) is positive-semidefinite.
- Parameters:
precision_tol (float, optional) – threshold value used to check if eigenvalues of the Choi operator \(\mathcal{J}\) are such that \(\textup{eigenvalues}(\mathcal{J}) >= - \textup{precision_tol}\). Note that this parameter can be set to negative values. Defaults to \(0.0\).
- Returns:
Positive-semidefinite condition.
- Return type:
- link_product(subscripts: str, second_network)[source]#
Link product between two quantum networks.
The link product is not commutative. Here, we assume that \(A.\textup{link_product}(B)\) means “applying \(B\) to \(A\)”. However, the
link_productis associative, so we override the @ operation in order to simplify notation.- Parameters:
subscripts (str, optional) – Specifies the subscript for summation using the Einstein summation convention. For more details, please refer to numpy.einsum.
second_network (
qibo.quantum_info.quantum_networks.QuantumNetwork) – Quantum network to be applied to the original network.
- Returns:
- Quantum network resulting
from the link product between two quantum networks.
- Return type:
- full(update: bool = False, backend=None)[source]#
Convert the internal representation to the full tensor of the network.
- Parameters:
update (bool, optional) – If
True, updates the internal representation of the network to the full tensor. Defaults toFalse.backend (
qibo.backends.abstract.Backend, optional) – Backend to be used in calculations. IfNone, defaults to the current backend. Defaults toNone.
- Returns:
full reprentation of the quantum network.
- Return type:
ndarray
- class qibo.quantum_info.quantum_networks.QuantumComb(tensor, partition: List[int] | Tuple[int] | None = None, system_input: List[bool] | Tuple[bool] | None = None, pure: bool = False, backend=None)[source]#
Stores a Quantum comb, which is a network in which the systems follows a sequential order.
It is also called the non-Markovian quantum process in many literatures. A quantum comb is a quantum network of the form \(J[┍i1┑,┕o1┙,┍i2┑,┕o2┙, ...]\), where the process first take an input state from system \(i1\), then output a state to system \(o1\), and so on. This is a non-Markovian process as the output of the system \(o2\) may depend on what happened in systems \(i1\), and \(o1\).
A quantum channel is a special case of quantum comb, where there are only one input system and one output system.
- Parameters:
tensor (ndarray) – the tensor representations of the quantum Comb.
system_input (List[bool] or Tuple[bool], optional) – mask on the input system of the Choi operator. If
None, defaults to(True,False,True,False,...), wherelen(system_input)=len(partition). Defaults toNone.pure (bool, optional) –
Truewhentensoris a “pure” representation (e.g. a pure state, a unitary operator, etc.),Falseotherwise. Defaults toFalse.backend (
qibo.backends.abstract.Backend, optional) – Backend to be used in calculations. IfNone, defaults to the current backend. Defaults toNone.
- is_causal(order: int | str | None = None, precision_tol: float = 1e-08)[source]#
Returns bool indicating if the Choi operator \(\mathcal{J}\) satisfies causal order
Causality is calculated based on a recursive constrains. This method reduce a n-comb to a (n-1)-comb at each step, and checks if the reduced comb is independent on the last output system.
- Parameters:
- Returns:
Causal order condition.
- Return type:
- classmethod from_operator(operator, partition=None, inverse=False, pure=False, backend=None)[source]#
Construct a
qibo.quantum_info.QuantumNetworkobject from a ndarray.This method converts a Choi operator to the internal representation of
qibo.quantum_info.quantum_networks.QuantumNetwork. The input array can be a pure state, a Choi operator, a unitary operator, etc.- Parameters:
arr (ndarray) – input numpy array.
partition (List[int] or Tuple[int], optional) – partition of
arr. IfNone, defaults to the shape ofarr. Defaults toNone.system_input (List[bool] or Tuple[bool], optional) – mask on the input system of the Choi operator. If
None, defaults to(True,False,True,False...), wherelen(system_input)=len(partition). Defaults toNone.pure (bool, optional) –
Truewhenarris a “pure” representation (e.g. a pure state, a unitary operator, etc.),Falseotherwise. Defaults toFalse.backend (
qibo.backends.abstract.Backend, optional) – Backend to be used in calculations. IfNone, defaults to the current backend. Defaults toNone.
- Returns:
quantum network constructed from the input Choi operator.
- Return type:
- class qibo.quantum_info.quantum_networks.QuantumChannel(tensor, partition: List[int] | Tuple[int] | None = None, system_input: List[bool] | Tuple[bool] | None = None, pure: bool = False, backend=None)[source]#
Stores a Quantum channel, which is a special case of quantum comb.
A quantum channel is a quantum comb with only one input and one output. This class includes all quantum channels, unitary operators, and quantum states.
To construct a QuantumChannel object, one can use the QuantumNetwork.from_nparray method. Note: if one try to construct a quantum network from a unitary operator or Choi operator, the first system will be the output. However, here we assume the first system is the input system. It is important to specify inverse=True when constructing by QuantumNetwork.from_nparray.
- Parameters:
tensor (ndarray) – the tensor representations of the quantum comb.
partition (List[int] or Tuple[int], optional) – partition of
matrix. If not provided and system_input is None, assume the input is a quantum state, whose input is a trivial system. If system_input is set to True, assume the input is an observable, whose output is a trivial system.system_input (List[bool] or Tuple[bool], optional) – mask on the input system of the Choi operator. If
Nonethe default is(True,False). Defaults toNone.pure (bool, optional) –
Truewhentensoris a “pure” representation (e.g. a pure state, a unitary operator, etc.),Falseotherwise. Defaults toFalse.backend (
qibo.backends.abstract.Backend, optional) – Backend to be used in calculations. IfNone, defaults to the current backend. Defaults toNone.
- is_unital(order: int | str | None = None, precision_tol: float = 1e-08)[source]#
Returns bool indicating if the Choi operator \(\mathcal{J}\) is unital.
A map is unital if it preserves the identity operator. Unitality is calculated as distance between the partial trace of \(\mathcal{J}\) and the Identity operator \(I\), with respect to a given norm. Default is the
Hilbert-Schmidtnorm (also known asFrobeniusnorm).For specifications on the other possible values of the parameter
orderfor thetensorflowbackend, please refer to tensorflow.norm. For all other backends, please refer to numpy.linalg.norm.- Parameters:
- Returns:
Unitality condition.
- Return type:
- is_channel(order: int | str | None = None, precision_tol_causal: float = 1e-08, precision_tol_psd: float = 1e-08)[source]#
Returns bool indicating if Choi operator \(\mathcal{E}\) is a channel.
- Parameters:
order (int or str, optional) – order of the norm used to calculate causality. Defaults to
None.precision_tol_causal (float, optional) – threshold \(\epsilon\) that defines if Choi operator of the network is \(\epsilon\)-close to causality in the norm given by
order. Defaults to \(10^{-8}\).precision_tol_psd (float, optional) – threshold value used to check if eigenvalues of the Choi operator \(\mathcal{E}\) are such that \(\textup{eigenvalues}(\mathcal{E}) >= \textup{precision_tol_psd}\). Note that this parameter can be set to negative values. Defaults to \(0.0\).
- Returns:
Channel condition.
- Return type:
Random Ensembles#
Functions that can generate random quantum objects.
Haar-random \(U_{3}\)#
- qibo.quantum_info.uniform_sampling_U3(ngates: int, seed=None, backend=None)[source]#
Samples parameters for Haar-random
qibo.gates.U3.- Parameters:
ngates (int) – Total number of \(U_{3}\) gates to be sampled.
seed (int or
numpy.random.Generator, optional) – Either a generator of random numbers or a fixed seed to initialize a generator. IfNone, initializes a generator with a random seed. Default:None.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
array of shape (
ngates, \(3\)).- Return type:
ndarray
Random Gaussian matrix#
- qibo.quantum_info.random_gaussian_matrix(dims: int, rank: int | None = None, mean: float = 0.0, stddev: float = 1.0, seed=None, backend=None)[source]#
Generates a random Gaussian Matrix.
Gaussian matrices are matrices where each entry is sampled from a Gaussian probability distribution
with mean \(\mu\) and standard deviation \(\sigma\).
- Parameters:
dims (int) – dimension of the matrix.
rank (int, optional) – rank of the matrix. If
None, thenrank == dims. Default:None.mean (float, optional) – mean of the Gaussian distribution. Defaults to 0.
stddev (float, optional) – standard deviation of the Gaussian distribution. Defaults to
1.seed (int or
numpy.random.Generator, optional) – Either a generator of random numbers or a fixed seed to initialize a generator. IfNone, initializes a generator with a random seed. Default:None.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Random Gaussian matrix with dimensions
(dims, rank).- Return type:
ndarray
Random Hermitian matrix#
- qibo.quantum_info.random_hermitian(dims: int, semidefinite: bool = False, normalize: bool = False, seed=None, backend=None)[source]#
Generates a random Hermitian matrix \(H\), i.e. a random matrix such that \(H = H^{\dagger}.\)
- Parameters:
dims (int) – dimension of the matrix.
semidefinite (bool, optional) – if
True, returns a Hermitian matrix that is also positive semidefinite. Defaults toFalse.normalize (bool, optional) – if
Trueandsemidefinite=False, returns a Hermitian matrix with eigenvalues in the interval \([-1, \, 1]\). IfTrueandsemidefinite=True, interval is \([0, \, 1]\). Defaults toFalse.seed (int or
numpy.random.Generator, optional) – Either a generator of random numbers or a fixed seed to initialize a generator. IfNone, initializes a generator with a random seed. Defaults toNone.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Hermitian matrix \(H\) with dimensions
(dims, dims).- Return type:
ndarray
Random unitary matrix#
- qibo.quantum_info.random_unitary(dims: int, measure: str | None = None, seed=None, backend=None)[source]#
Returns a random Unitary operator \(U\), i.e. a random operator such that \(U^{-1} = U^{\dagger}\).
- Parameters:
dims (int) – dimension of the matrix.
measure (str, optional) – probability measure in which to sample the unitary from. If
None, functions returns \(\exp{(-i \, H)}\), where \(H\) is a Hermitian operator. If"haar", returns an Unitary matrix sampled from the Haar measure. Defaults toNone.seed (int or
numpy.random.Generator, optional) – Either a generator of random numbers or a fixed seed to initialize a generator. IfNone, initializes a generator with a random seed. Defaults toNone.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Unitary matrix \(U\) with dimensions
(dims, dims).- Return type:
ndarray
Random quantum channel#
- qibo.quantum_info.random_quantum_channel(dims: int, representation: str = 'liouville', measure: str | None = None, rank: int | None = None, order: str = 'row', normalize: bool = False, precision_tol: float | None = None, validate_cp: bool = True, nqubits: int | None = None, initial_state_env=None, seed=None, backend=None)[source]#
Creates a random superoperator from an unitary operator in one of the supported superoperator representations.
- Parameters:
dims (int) – dimension of the \(n\)-qubit operator, i.e. \(\text{dims}=2^{n}\).
representation (str, optional) – If
"chi", returns a random channel in the Chi representation. If"choi", returns channel in Choi representation. If"kraus", returns Kraus representation of channel. If"liouville", returns Liouville representation. If"pauli", returns Pauli-Liouville representation. If “pauli-<pauli_order>” or “chi-<pauli_order>”, (e.g. “pauli-IZXY”), returns it in the Pauli basis with the corresponding order of single-qubit Pauli elements (seeqibo.quantum_info.pauli_basis()). If"stinespring", returns random channel in the Stinespring representation. Defaults to"liouville".measure (str, optional) – probability measure in which to sample the unitary from. If
None, functions returns \(\exp{(-i \, H)}\), where \(H\) is a Hermitian operator. If"haar", returns an Unitary matrix sampled from the Haar measure. If"bcsz", it samples an unitary from the BCSZ distribution with Krausrank. Defaults toNone.rank (int, optional) – used when
measure=="bcsz". Rank of the matrix. IfNone, thenrank==dims. Defaults toNone.order (str, optional) – If
"row", vectorization is performed row-wise. If"column", vectorization is performed column-wise. If"system", a block-vectorization is performed. Defaults to"row".normalize (bool, optional) – used when
representation="chi"orrepresentation="pauli". IfTrueassumes the normalized Pauli basis. IfFalse, it assumes unnormalized Pauli basis. Defaults toFalse.precision_tol (float, optional) – if
representation="kraus", it is the precision tolerance for eigenvalues found in the spectral decomposition problem. Any eigenvalue \(\lambda <\)precision_tolis set to 0 (zero). IfNone,precision_toldefaults toqibo.config.PRECISION_TOL=1e-8. Defaults toNone.validate_cp (bool, optional) – used when
representation="stinespring". IfTrue, checks if the Choi representation of superoperator used as intermediate step is a completely positive map. IfFalse, it assumes that it is completely positive (and Hermitian). Defaults toTrue.nqubits (int, optional) – used when
representation="stinespring". Total number of qubits in the system that is interacting with the environment. Must be equal or greater than the number of qubits that Kraus representation of the system superoperator acts on. IfNone, defaults to the number of qubits in the Kraus operators. Defauts toNone.initial_state_env (ndarray, optional) – used when
representation="stinespring". Statevector representing the initial state of the enviroment. IfNone, it assumes the environment in its ground state. Defaults toNone.seed (int or
numpy.random.Generator, optional) – Either a generator of random numbers or a fixed seed to initialize a generator. IfNone, initializes a generator with a random seed. Defaults toNone.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Superoperator representation of a random unitary gate.
- Return type:
ndarray
Random statevector#
- qibo.quantum_info.random_statevector(dims: int, dtype=None, seed=None, backend=None)[source]#
Creates a random statevector \(\ket{\psi}\).
\[\ket{\psi} = \sum_{k = 0}^{d - 1} \, \sqrt{p_{k}} \, e^{i \phi_{k}} \, \ket{k} \, ,\]where \(d\) is
dims, and \(p_{k}\) and \(\phi_{k}\) are, respectively, the probability and phase corresponding to the computational basis state \(\ket{k}\).Note
If
dtypeif"float64","float32", or an equivalent type, then \(\ket{\psi} \in \mathbb{R}^{\text{dims}}\). Otherwise, \(\ket{\psi} \in \mathbb{C}^{\text{dims}}\).- Parameters:
dims (int) – dimension of the matrix.
dtype (str or type, optional) – data type for the random statevector. Options are
"complex128,"complex64","float64", or"float32". It also accepts the equivalent data types ofbackend’s engines, e.g.numpy.complex128orcupy.float64. IfNone, defaults tobackend.dtype. Defaults toNone.seed (int or
numpy.random.Generator, optional) – Either a generator of random numbers or a fixed seed to initialize a generator. IfNone, initializes a generator with a random seed. Defaults toNone.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Random statevector \(\ket{\psi}\).
- Return type:
ndarray
Random density matrix#
- qibo.quantum_info.random_density_matrix(dims: int, rank: int | None = None, pure: bool = False, metric: str = 'hilbert-schmidt', basis: str | None = None, normalize: bool = False, order: str = 'row', seed=None, backend=None)[source]#
Creates a random density matrix \(\rho\). If
pure=True,\[\rho = \ketbra{\psi}{\psi} \, ,\]where \(\ket{\psi}\) is a
qibo.quantum_info.random_statevector(). Ifpure=False, then\[\rho = \sum_{k} \, p_{k} \, \ketbra{\psi_{k}}{\psi_{k}} \, .\]is a mixed state.
- Parameters:
dims (int) – dimension of the matrix.
rank (int, optional) – rank of the matrix. If
None, thenrank == dims. Defaults toNone.pure (bool, optional) – if
True, returns a pure state. Defaults toFalse.metric (str, optional) – metric to sample the density matrix from. Options:
"hilbert-schmidt","ginibre", and"bures". Note that, by definition,rankdefaults toNonewhenmetric=="hilbert-schmidt". Defaults to"hilbert-schmidt".basis (str, optional) – if
None, returns random density matrix in the computational basis. If"pauli-<pauli_order>", (e.g."pauli-IZXY"), returns it in the Pauli basis with the corresponding order of single-qubit Pauli elements (seeqibo.quantum_info.pauli_basis()). Defaults toNone.normalize (bool, optional) – used when
basis="pauli-<pauli-order>". IfTruereturns random density matrix in the normalized Pauli basis. IfFalse, returns state in the unnormalized Pauli basis. Defaults toFalse.order (str, optional) – used when
basis="pauli-<pauli-order>". If"row", vectorization of Pauli basis is performed row-wise. If"column", vectorization is performed column-wise. If"system", system-wise vectorization is performed. Default is"row".seed (int or
numpy.random.Generator, optional) – Either a generator of random numbers or a fixed seed to initialize a generator. IfNone, initializes a generator with a random seed. Defaults toNone.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Random density matrix \(\rho\).
- Return type:
ndarray
Random Clifford#
- qibo.quantum_info.random_clifford(nqubits: int, return_circuit: bool = True, seed=None, backend=None, **kwargs)[source]#
Generates a random \(n\)-qubit Clifford operator, where \(n\) is
nqubits. For the mathematical details, see Reference [1].- Parameters:
nqubits (int) – number of qubits.
return_circuit (bool, optional) – if
True, returns aqibo.models.Circuitobject. IfFalse, returns anndarrayobject. Defaults toTrue.seed (int or
numpy.random.Generator, optional) – Either a generator of random numbers or a fixed seed to initialize a generator. IfNone, initializes a generator with a random seed. Defaults toNone.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.kwargs (dict, optional) – Additional arguments used to initialize a Circuit object. For details, see the documentation of
qibo.models.circuit.Circuit.
- Returns:
Random Clifford operator.
- Return type:
qibo.quantum_info.clifford.Cliffordorqibo.models.Circuit
- Reference:
S. Bravyi and D. Maslov, Hadamard-free circuits expose the structure of the Clifford group. arXiv:2003.09412 [quant-ph].
Random Pauli#
- qibo.quantum_info.random_pauli(qubits, depth: int, max_qubits: int | None = None, subset: list | None = None, return_circuit: bool = True, density_matrix: bool = False, seed=None, backend=None)[source]#
Creates random Pauli operator(s).
Pauli operators are sampled from the single-qubit Pauli set \(\{I, \, X, \, Y, \, Z\}\).
- Parameters:
qubits (int or list or ndarray) – if
intandmax_qubits=None, the number of qubits. Ifintandmax_qubits != None, qubit index in which the Pauli sequence will act. Iflistorndarray, indexes of the qubits for the Pauli sequence to act.depth (int) – length of the sequence of Pauli gates.
max_qubits (int, optional) – total number of qubits in the circuit. If
None,max_qubits = max(qubits). Defaults toNone.subset (list, optional) – list containing a subset of the 4 single-qubit Pauli operators. If
None, defaults to the complete set. Defaults toNone.return_circuit (bool, optional) – if
True, returns aqibo.models.Circuitobject. IfFalse, returns anndarraywith shape (qubits, depth, 2, 2) that contains all Pauli matrices that were sampled. Defaults toTrue.density_matrix (bool, optional) – used when
return_circuit=True. If True, the circuit would evolve density matrices. Defaults toFalse.seed (int or
numpy.random.Generator, optional) – Either a generator of random numbers or a fixed seed to initialize a generator. IfNone, initializes a generator with a random seed. Defaults toNone.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
all sampled Pauli operators.
- Return type:
(ndarray or
qibo.models.Circuit)
Random Pauli Hamiltonian#
- qibo.quantum_info.random_pauli_hamiltonian(nqubits: int, max_eigenvalue: int | float | None = None, normalize: bool = False, pauli_order: str = 'IXYZ', seed=None, backend=None)[source]#
Generates a random Hamiltonian in the Pauli basis.
- Parameters:
nqubits (int) – number of qubits.
max_eigenvalue (int or float, optional) – fixes the value of the largest eigenvalue. Defaults to
None.normalize (bool, optional) – If
True, fixes the gap of the Hamiltonian as1.0. Moreover, ifTrue, thenmax_eigenvaluemust be> 1.0. Defaults toFalse.pauli_order (str, optional) – corresponds to the order of 4 single-qubit Pauli elements in the basis. Defaults to “IXYZ”.
seed (int or
numpy.random.Generator, optional) – Either a generator of random numbers or a fixed seed to initialize a generator. IfNone, initializes a generator with a random seed. Defaults toNone.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Hamiltonian in the Pauli basis and its corresponding eigenvalues.
- Return type:
tuple(ndarray, ndarray)
Random stochastic matrix#
- qibo.quantum_info.random_stochastic_matrix(dims: int, bistochastic: bool = False, diagonally_dominant: bool = False, precision_tol: float | None = None, max_iterations: int | None = None, seed=None, backend=None)[source]#
Creates a random stochastic matrix.
- Parameters:
dims (int) – dimension of the matrix.
bistochastic (bool, optional) – if
True, matrix is row- and column-stochastic. IfFalse, matrix is row-stochastic. Defaults toFalse.diagonally_dominant (bool, optional) – if
True, matrix is strictly diagonally dominant. Defaults toFalse.precision_tol (float, optional) – tolerance level for how much each probability distribution can deviate from summing up to
1.0. IfNone, it defaults toqibo.config.PRECISION_TOL. Defaults toNone.max_iterations (int, optional) – when
bistochastic=True, maximum number of iterations used to normalize all rows and columns simultaneously. IfNone, defaults toqibo.config.MAX_ITERATIONS. Defaults toNone.seed (int or
numpy.random.Generator, optional) – Either a generator of random numbers or a fixed seed to initialize a generator. IfNone, initializes a statevectorgenerator with a random seed. Defaults toNone.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
a random stochastic matrix.
- Return type:
ndarray
Superoperator Transformations#
Functions used to convert superoperators among their possible representations. For more in-depth theoretical description of the representations and transformations, we direct the reader to Wood, Biamonte, and Cory, Quant. Inf. Comp. 15, 0579-0811 (2015).
Vectorization#
- qibo.quantum_info.vectorization(state, order: str = 'row', backend=None)[source]#
Returns state \(\rho\) in its Liouville representation \(|\rho)\).
If
order="row", then:\[|\rho) = \sum_{k, l} \, \rho_{kl} \, \ket{k} \otimes \ket{l} \, .\]If
order="column", then:\[|\rho) = \sum_{k, l} \, \rho_{kl} \, \ket{l} \otimes \ket{k} \, .\]If
stateis a 3-dimensional tensor, it is interpreted as a batch of states.- Parameters:
state (ndarray) – statevector, density matrix, an array of statevectors, or an array of density matrices.
order (str, optional) – If
"row", vectorization is performed row-wise. If"column", vectorization is performed column-wise. If"system", a block-vectorization is performed. Defaults to"row".backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Liouville representation of
state.- Return type:
ndarray
Note
Due to numpy limitations on handling transposition of tensors,
this function will not work when the number of qubits \(n\)
is such that \(n > 16\).
Unvectorization#
- qibo.quantum_info.unvectorization(state, order: str = 'row', backend=None)[source]#
Returns state \(\rho\) from its Liouville representation \(|\rho)\). This operation is the inverse function of
vectorization(), i.e.\[\begin{split}\begin{align} \rho &= \text{unvectorization}(|\rho)) \nonumber \\ &= \text{unvectorization}(\text{vectorization}(\rho)) \nonumber \end{align}\end{split}\]If
statehas shape (N, k), it is interpreted as a batch of states.- Parameters:
state – quantum state or batch of states in the Liouville representation.
order (str, optional) – If
"row", unvectorization is performed row-wise. If"column", unvectorization is performed column-wise. If"system", system-wise vectorization is performed. Defaults to"row".backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Density matrix of
state.- Return type:
ndarray
Note
Due to numpy limitations on handling transposition of tensors,
this function will not work when the number of qubits \(n\)
is such that \(n > 16\).
To Choi#
- qibo.quantum_info.to_choi(channel, order: str = 'row', backend=None)[source]#
Converts quantum
channel\(U\) to its Choi representation \(\Lambda\).\[\Lambda = | U ) ( U | \, ,\]where \(| \cdot )\) is the
qibo.quantum_info.vectorization()operation.- Parameters:
channel (ndarray) – quantum channel.
order (str, optional) – If
"row", vectorization is performed row-wise. If"column", vectorization is performed column-wise. If"system", a block-vectorization is performed. Default is"row".backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
quantum channel in its Choi representation.
- Return type:
ndarray
To Liouville#
- qibo.quantum_info.to_liouville(channel, order: str = 'row', backend=None)[source]#
Converts quantum
channel\(U\) to its Liouville representation \(\mathcal{E}\). It uses the Choi representation as an intermediate step.- Parameters:
channel (ndarray) – quantum channel.
order (str, optional) – If
"row", vectorization is performed row-wise. If"column", vectorization is performed column-wise. If"system", a block-vectorization is performed. Default is"row".backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
quantum channel in its Liouville representation.
- Return type:
ndarray
To Pauli-Liouville#
- qibo.quantum_info.to_pauli_liouville(channel, normalize: bool = False, order: str = 'row', pauli_order: str = 'IXYZ', backend=None)[source]#
Converts quantum
channel\(U\) to its Pauli-Liouville representation \(\mathcal{E}\). It uses the Liouville representation as an intermediate step.- Parameters:
channel (ndarray) – quantum channel.
normalize (bool, optional) – If
Truesuperoperator is returned in the normalized Pauli basis. IfFalse, it is returned in the unnormalized Pauli basis. Defaults toFalse.order (str, optional) – If
"row", vectorization is performed row-wise. If"column", vectorization is performed column-wise. If"system", a block-vectorization is performed. Default is"row".pauli_order (str, optional) – corresponds to the order of 4 single-qubit Pauli elements. Default is “IXYZ”.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
quantum channel in its Pauli-Liouville representation.
- Return type:
ndarray
To Chi#
- qibo.quantum_info.to_chi(channel, normalize: bool = False, order: str = 'row', pauli_order: str = 'IXYZ', backend=None)[source]#
Converts quantum
channel\(U\) to its \(\chi\)-representation.- Parameters:
channel (ndarray) – quantum channel.
normalize (bool, optional) – If
Truesuperoperator is returned in the normalized Pauli basis. IfFalse, it is returned in the unnormalized Pauli basis. Defaults toFalse.order (str, optional) – If
"row", vectorization is performed row-wise. If"column", vectorization is performed column-wise. If"system", a block-vectorization is performed. Default is"row".pauli_order (str, optional) – corresponds to the order of 4 single-qubit Pauli elements. Default is “IXYZ”.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
quantum channel in its \(\chi\)-representation.
- Return type:
ndarray
To Stinespring#
- qibo.quantum_info.to_stinespring(channel, partition: List[int] | Tuple[int, ...] | None = None, nqubits: int | None = None, initial_state_env=None, backend=None)[source]#
Convert quantum
channel\(U\) to its Stinespring representation \(U_{0}\).It uses the Kraus representation as an intermediate step.
- Parameters:
channel (ndarray) – quantum channel.
nqubits (int, optional) – total number of qubits in the system that is interacting with the environment. Must be equal or greater than the number of qubits
channelacts on. IfNone, defaults to the number of qubits inchannel. Defauts toNone.initial_state_env (ndarray, optional) – statevector representing the initial state of the enviroment. If
None, it assumes the environment in its ground state. Defaults toNone.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it usesqibo.backends.GlobalBackend. Defaults toNone.
- Returns:
Quantum channel in its Stinespring representation \(U_{0}\).
- Return type:
ndarray
Choi to Liouville#
- qibo.quantum_info.choi_to_liouville(choi_super_op, order: str = 'row', backend=None)[source]#
Converts Choi representation \(\Lambda\) of quantum channel to its Liouville representation \(\mathcal{E}\).
If
order="row", then:\[\Lambda_{\alpha\beta, \, \gamma\delta} \mapsto \Lambda_{\alpha\gamma, \, \beta\delta} \equiv \mathcal{E}\]If
order="column", then:\[\Lambda_{\alpha\beta, \, \gamma\delta} \mapsto \Lambda_{\delta\beta, \, \gamma\alpha} \equiv \mathcal{E}\]- Parameters:
choi_super_op – Choi representation of quantum channel.
order (str, optional) – If
"row", reshuffling is performed with respect to row-wise vectorization. If"column", reshuffling is performed with respect to column-wise vectorization. If"system", operator is converted to a representation based on row vectorization, reshuffled, and then converted back to its representation with respect to system-wise vectorization. Defaults to"row".backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Liouville representation of quantum channel.
- Return type:
ndarray
Choi to Pauli-Liouville#
- qibo.quantum_info.choi_to_pauli(choi_super_op, normalize: bool = False, order: str = 'row', pauli_order: str = 'IXYZ', backend=None)[source]#
Converts Choi representation \(\Lambda\) of a quantum channel to its Pauli-Liouville representation.
- Parameters:
choi_super_op (ndarray) – superoperator in the Choi representation.
normalize (bool, optional) – If
Truesuperoperator is returned in the normalized Pauli basis. IfFalse, it is returned in the unnormalized Pauli basis. Defaults toFalse.order (str, optional) – If
"row", it assumeschoi_super_opis in row-vectorization. If"column", it assumes column-vectorization. Defaults to"row".pauli_order (str, optional) – corresponds to the order of 4 single-qubit Pauli elements. Defaults to “IXYZ”.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
superoperator in the Pauli-Liouville representation.
- Return type:
ndarray
Choi to Kraus#
- qibo.quantum_info.superoperator_transformations.choi_to_kraus(choi_super_op, precision_tol: float | None = None, order: str = 'row', validate_cp: bool = True, backend=None)[source]#
Converts Choi representation \(\Lambda\) of a quantum channel \(\mathcal{E}\) into Kraus operators \(\{ K_{\alpha} \}_{\alpha}\).
If \(\mathcal{E}\) is a completely positive (CP) map, then
\[\Lambda = \sum_{\alpha} \, \lambda_{\alpha}^{2} \, |\tilde{K}_{\alpha})(\tilde{K}_{\alpha}| \, .\]where \(|\cdot)\) is the
qibo.quantum_info.vectorization()operation.This is the spectral decomposition of \(\Lambda\), Hence, the set \(\{\lambda_{\alpha}, \, \tilde{K}_{\alpha}\}_{\alpha}\) is found by diagonalization of \(\Lambda\). The Kraus operators \(\{K_{\alpha}\}_{\alpha}\) are defined as
\[K_{\alpha} = \lambda_{\alpha} \, \text{unvectorization}(|\tilde{K}_{\alpha})) \, .\]If \(\mathcal{E}\) is not CP, then spectral composition is replaced by a singular value decomposition (SVD), i.e.
\[\Lambda = U \, S \, V^{\dagger} \, ,\]where \(U\) is a \(d^{2} \times d^{2}\) unitary matrix, \(S\) is a \(d^{2} \times d^{2}\) positive diagonal matrix containing the singular values of \(\Lambda\), and \(V\) is a \(d^{2} \times d^{2}\) unitary matrix. The Kraus coefficients are replaced by the square root of the singular values, and \(U\) (\(V\)) determine the left-generalized (right-generalized) Kraus operators.
- Parameters:
choi_super_op – Choi representation of a quantum channel.
precision_tol (float, optional) – Precision tolerance for eigenvalues found in the spectral decomposition problem. Any eigenvalue \(\lambda <\)
precision_tolis set to 0 (zero). IfNone,precision_toldefaults toqibo.config.PRECISION_TOL=1e-8. Defaults toNone.order (str, optional) – If
"row", reshuffling is performed with respect to row-wise vectorization. If"column", reshuffling is performed with respect to column-wise vectorization. If"system", operator is converted to a representation based on row vectorization, reshuffled, and then converted back to its representation with respect to system-wise vectorization. Defaults to"row".validate_cp (bool, optional) – If
True, checks ifchoi_super_opis a completely positive map. IfFalse, it assumes thatchoi_super_opis completely positive (and Hermitian). Defaults toTrue.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
The set \(\{K_{\alpha}, \, \lambda_{\alpha} \}_{\alpha}\) of Kraus operators representing the quantum channel and their respective coefficients. If map is non-CP, then function returns the set \(\{ \{K_{L}, \, K_{R}\}_{\alpha}, \, \lambda_{\alpha} \}_{\alpha}\), with the left- and right-generalized Kraus operators as well as the square root of their corresponding singular values.
- Return type:
tuple(ndarray, ndarray)
Note
Due to the spectral decomposition subroutine in this function, the resulting Kraus operators \(\{K_{\alpha}\}_{\alpha}\) might contain global phases. That implies these operators are not exactly equal to the “true” Kraus operators \(\{K_{\alpha}^{(\text{ideal})}\}_{\alpha}\). However, since these are global phases, the operators’ actions are the same, i.e.
Note
User can set validate_cp=False in order to speed up execution by not checking if
input map choi_super_op is completely positive (CP) and Hermitian. However, that may
lead to erroneous outputs if choi_super_op is not guaranteed to be CP. We advise users
to either set this flag carefully or leave it in its default setting (validate_cp=True).
Choi to Chi-matrix#
- qibo.quantum_info.choi_to_chi(choi_super_op, normalize: bool = False, order: str = 'row', pauli_order: str = 'IXYZ', backend=None)[source]#
Converts Choi representation \(\Lambda\) of quantum channel to its \(\chi\)-matrix representation.
\[\chi = \text{liouville_to_pauli}(\Lambda)\]- Parameters:
choi_super_op – Choi representation of a quantum channel.
normalize (bool, optional) – If
Trueassumes the normalized Pauli basis. IfFalse, it assumes unnormalized Pauli basis. Defaults toFalse.order (str, optional) – If
"row", reshuffling is performed with respect to row-wise vectorization. If"column", reshuffling is performed with respect to column-wise vectorization. If"system", operator is converted to a representation based on row vectorization, reshuffled, and then converted back to its representation with respect to system-wise vectorization. Defaults to"row".pauli_order (str, optional) – corresponds to the order of 4 single-qubit Pauli elements. Defaults to “IXYZ”.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Chi-matrix representation of the quantum channel.
- Return type:
ndarray
Choi to Stinespring#
- qibo.quantum_info.choi_to_stinespring(choi_super_op, precision_tol: float | None = None, order: str = 'row', validate_cp: bool = True, nqubits: int | None = None, initial_state_env=None, backend=None)[source]#
Converts Choi representation \(\Lambda\) of quantum channel to its Stinespring representation \(U_{0}\). It uses the Kraus representation as an intermediate step.
- Parameters:
choi_super_op – Choi representation of a quantum channel.
precision_tol (float, optional) – Precision tolerance for eigenvalues found in the spectral decomposition problem. Any eigenvalue \(\lambda <\)
precision_tolis set to 0 (zero). IfNone,precision_toldefaults toqibo.config.PRECISION_TOL=1e-8. Defaults toNone.order (str, optional) – If
"row", reshuffling is performed with respect to row-wise vectorization. If"column", reshuffling is performed with respect to column-wise vectorization. If"system", operator is converted to a representation based on row vectorization, reshuffled, and then converted back to its representation with respect to system-wise vectorization. Defaults to"row".validate_cp (bool, optional) – If
True, checks ifchoi_super_opis a completely positive map. IfFalse, it assumes thatchoi_super_opis completely positive (and Hermitian). Defaults toTrue.nqubits (int, optional) – total number of qubits in the system that is interacting with the environment. Must be equal or greater than the number of qubits
kraus_opsacts on. IfNone, defaults to the number of qubits inkraus_ops. Defauts toNone.initial_state_env (ndarray, optional) – statevector representing the initial state of the enviroment. If
None, it assumes the environment in its ground state. Defaults toNone.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Choi representation of quantum channel.
- Return type:
ndarray
Kraus to Choi#
- qibo.quantum_info.kraus_to_choi(kraus_ops, order: str = 'row', backend=None)[source]#
Converts Kraus representation \(\{K_{\alpha}\}_{\alpha}\) of quantum channel to its Choi representation \(\Lambda\).
\[\Lambda = \sum_{\alpha} \, |K_{\alpha})( K_{\alpha}|\]where \(|K_{\alpha})\) is the vectorization of the Kraus operator \(K_{\alpha}\). For a definition of vectorization, see
qibo.quantum_info.vectorization().- Parameters:
kraus_ops (list) – List of Kraus operators as pairs
(qubits, Ak)wherequbitsrefers the qubit ids that \(A_k\) acts on and \(A_k\) is the corresponding matrix as anp.ndarray.order (str, optional) – If
"row", reshuffling is performed with respect to row-wise vectorization. If"column", reshuffling is performed with respect to column-wise vectorization. If"system", operator is converted to a representation based on row vectorization, reshuffled, and then converted back to its representation with respect to system-wise vectorization. Defaults to"row".backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Choi representation of the Kraus channel.
- Return type:
ndarray
Kraus to Liouville#
- qibo.quantum_info.kraus_to_liouville(kraus_ops, order: str = 'row', backend=None)[source]#
Converts from Kraus representation \(\{K_{\alpha}\}_{\alpha}\) of quantum channel to its Liouville representation \(\mathcal{E}\). It uses the Choi representation as an intermediate step.
\[\mathcal{E} = \text{choi_to_liouville}(\text{kraus_to_choi} (\{K_{\alpha}\}_{\alpha}))\]- Parameters:
kraus_ops (list) – List of Kraus operators as pairs
(qubits, Ak)wherequbitsrefers the qubit ids that \(A_k\) acts on and \(A_k\) is the corresponding matrix as anp.ndarray.order (str, optional) – If
"row", reshuffling is performed with respect to row-wise vectorization. If"column", reshuffling is performed with respect to column-wise vectorization. If"system", operator is converted to a representation based on row vectorization, reshuffled, and then converted back to its representation with respect to system-wise vectorization. Defaults to"row".backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Liouville representation of quantum channel.
- Return type:
ndarray
Kraus to Pauli-Liouville#
- qibo.quantum_info.kraus_to_pauli(kraus_ops, normalize: bool = False, order: str = 'row', pauli_order: str = 'IXYZ', backend=None)[source]#
Converts Kraus representation \(\{K_{\alpha}\}_{\alpha}\) of a quantum channel to its Pauli-Liouville representation.
- Parameters:
kraus_ops (list) – List of Kraus operators as pairs
(qubits, Ak)wherequbitsrefers the qubit ids that \(A_k\) acts on and \(A_k\) is the corresponding matrix as anp.ndarray.normalize (bool, optional) – If
Truesuperoperator is returned in the normalized Pauli basis. IfFalse, it is returned in the unnormalized Pauli basis. Defaults toFalse.order (str, optional) – If
"row", intermediate step for Choi representation is done in row-vectorization. If"column", step is done in column-vectorization. If"system", block-vectorization is performed. Defaults to"row".pauli_order (str, optional) – corresponds to the order of 4 single-qubit Pauli elements. Defaults to “IXYZ”.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
superoperator in the Pauli-Liouville representation.
- Return type:
ndarray
Kraus to Chi-matrix#
- qibo.quantum_info.kraus_to_chi(kraus_ops, normalize: bool = False, order: str = 'row', pauli_order: str = 'IXYZ', backend=None)[source]#
Convert Kraus representation \(\{K_{\alpha}\}_{\alpha}\) of quantum channel to its \(\chi\)-matrix representation.
\[\chi = \sum_{\alpha} \, |c_{\alpha})( c_{\alpha}|,\]where \(|c_{\alpha}) \cong |K_{\alpha})\) in Pauli-Liouville basis, and \(| \cdot )\) is the
qibo.quantum_info.vectorization()operation.- Parameters:
kraus_ops (list) – List of Kraus operators as pairs
(qubits, Ak)wherequbitsrefers the qubit ids that \(A_k\) acts on and \(A_k\) is the corresponding matrix as anp.ndarray.normalize (bool, optional) – If
Trueassumes the normalized Pauli basis. IfFalse, it assumes unnormalized Pauli basis. Defaults toFalse.order (str, optional) – If
"row", reshuffling is performed with respect to row-wise vectorization. If"column", reshuffling is performed with respect to column-wise vectorization. If"system", operator is converted to a representation based on row vectorization, reshuffled, and then converted back to its representation with respect to system-wise vectorization. Defaults to"row".pauli_order (str, optional) – corresponds to the order of 4 single-qubit Pauli elements in the Pauli basis. Defaults to “IXYZ”.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Chi-matrix representation of the Kraus channel.
- Return type:
ndarray
Kraus to Stinespring#
- qibo.quantum_info.kraus_to_stinespring(kraus_ops, nqubits: int | None = None, initial_state_env=None, backend=None)[source]#
Converts Kraus representation \(\{K_{\alpha}\}_{\alpha}\) of quantum channel to its Stinespring representation \(U_{0}\), i.e.
\[U_{0} = \sum_{\alpha} \, K_{\alpha} \otimes \ketbra{\alpha}{v_{0}} \, ,\]where \(\ket{v_{0}}\) is the initial state of the environment (
initial_state_env), \(D\) is the dimension of the environment’s Hilbert space, and \(\{\ket{\alpha} \, : \, \alpha = 0, 1, \cdots, D - 1 \}\) is an orthonormal basis for the environment’s space.- Parameters:
kraus_ops (list) – List of Kraus operators as pairs
(qubits, Ak)wherequbitsrefers the qubit ids that \(A_k\) acts on and \(A_k\) is the corresponding matrix as anp.ndarray.nqubits (int, optional) – total number of qubits in the system that is interacting with the environment. Must be equal or greater than the number of qubits
kraus_opsacts on. IfNone, defaults to the number of qubits inkraus_ops. Defauts toNone.initial_state_env (ndarray, optional) – statevector representing the initial state of the enviroment. If
None, it assumes the environment in its ground state. Defaults toNone.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Stinespring representation (restricted unitary) of the Kraus channel.
- Return type:
ndarray
Liouville to Choi#
- qibo.quantum_info.liouville_to_choi(super_op, order: str = 'row', backend=None)[source]#
Converts Liouville representation of quantum channel \(\mathcal{E}\) to its Choi representation \(\Lambda\). Indexing \(\mathcal{E}\) as \(\mathcal{E}_{\alpha\beta, \, \gamma\delta} \,\,\), then
If
order="row":\[\Lambda = \sum_{k, l} \, \ketbra{k}{l} \otimes \mathcal{E}(\ketbra{k}{l}) \equiv \mathcal{E}_{\alpha\gamma, \, \beta\delta}\]If
order="column", then:\[\Lambda = \sum_{k, l} \, \mathcal{E}(\ketbra{k}{l}) \otimes \ketbra{k}{l} \equiv \mathcal{E}_{\delta\beta, \, \gamma\alpha}\]- Parameters:
super_op – Liouville representation of quantum channel.
order (str, optional) – If
"row", reshuffling is performed with respect to row-wise vectorization. If"column", reshuffling is performed with respect to column-wise vectorization. If"system", operator is converted to a representation based on row vectorization, reshuffled, and then converted back to its representation with respect to system-wise vectorization. Defaults to"row".backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Choi representation of quantum channel.
- Return type:
ndarray
Liouville to Pauli-Liouville#
- qibo.quantum_info.liouville_to_pauli(super_op, normalize: bool = False, order: str = 'row', pauli_order: str = 'IXYZ', backend=None)[source]#
Converts Liouville representation \(\mathcal{E}\) of a quantum channel to its Pauli-Liouville representation.
- Parameters:
super_op (ndarray) – superoperator in the Liouville representation._
normalize (bool, optional) – If
Truesuperoperator is returned in the normalized Pauli basis. IfFalse, it is returned in the unnormalized Pauli basis. Defaults toFalse.order (str, optional) – If
"row", it assumessuper_opis in row-vectorization. If"column", it assumes column-vectorization. If"system", it assumes block-vectorization. Defaults to"row".pauli_order (str, optional) – corresponds to the order of 4 single-qubit Pauli elements in the basis. Defaults to “IXYZ”.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
superoperator in the Pauli-Liouville representation.
- Return type:
ndarray
Liouville to Kraus#
- qibo.quantum_info.liouville_to_kraus(super_op, precision_tol: float | None = None, order: str = 'row', backend=None)[source]#
Converts Liouville representation \(\mathcal{E}\) of a quantum channel to its Kraus representation \(\{K_{\alpha}\}_{\alpha}\). It uses the Choi representation as an intermediate step.
\[\{K_{\alpha}, \, \lambda_{\alpha}\}_{\alpha} = \text{choi_to_kraus}(\text{liouville_to_choi}(\mathcal{E}))\]- Parameters:
super_op (ndarray) – Liouville representation of quantum channel.
precision_tol (float, optional) – Precision tolerance for eigenvalues found in the spectral decomposition problem. Any eigenvalue \(\lambda < \text{precision_tol}\) is set to 0 (zero). If
None,precision_toldefaults toqibo.config.PRECISION_TOL=1e-8. Defaults to None.order (str, optional) – If
"row", reshuffling is performed with respect to row-wise vectorization. If"column", reshuffling is performed with respect to column-wise vectorization. If"system", operator is converted to a representation based on row vectorization, reshuffled, and then converted back to its representation with respect to system-wise vectorization. Defaults to"row".backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Kraus operators of quantum channel and their respective coefficients.
- Return type:
(ndarray, ndarray)
Note
Due to the spectral decomposition subroutine in this function, the resulting Kraus operators \(\{K_{\alpha}\}_{\alpha}\) might contain global phases. That implies these operators are not exactly equal to the “true” Kraus operators \(\{K_{\alpha}^{(\text{ideal})}\}_{\alpha}\). However, since these are global phases, the operators’ actions are the same, i.e.
Liouville to Chi-matrix#
- qibo.quantum_info.liouville_to_chi(super_op, normalize: bool = False, order: str = 'row', pauli_order: str = 'IXYZ', backend=None)[source]#
Converts Liouville representation of quantum channel \(\mathcal{E}\) to its \(\chi\)-matrix representation. It uses the Choi representation as an intermediate step.
\[\chi = \text{liouville_to_pauli}(\text{liouville_to_choi}(\mathcal{E}))\]- Parameters:
super_op – Liouville representation of quantum channel.
normalize (bool, optional) – If
Trueassumes the normalized Pauli basis. IfFalse, it assumes unnormalized Pauli basis. Defaults toFalse.order (str, optional) – If
"row", reshuffling is performed with respect to row-wise vectorization. If"column", reshuffling is performed with respect to column-wise vectorization. If"system", operator is converted to a representation based on row vectorization, reshuffled, and then converted back to its representation with respect to system-wise vectorization. Defaults to"row".pauli_order (str, optional) – corresponds to the order of 4 single-qubit Pauli elements in the basis. Defaults to “IXYZ”.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Chi-matrix representation of quantum channel.
- Return type:
ndarray
Liouville to Stinespring#
- qibo.quantum_info.liouville_to_stinespring(super_op, order: str = 'row', precision_tol: float | None = None, validate_cp: bool = True, nqubits: int | None = None, initial_state_env=None, backend=None)[source]#
Converts Liouville representation \(\mathcal{E}\) of quantum channel to its Stinespring representation \(U_{0}\). It uses the Choi representation \(\Lambda\) as intermediate step.
- Parameters:
super_op – Liouville representation of quantum channel.
order (str, optional) – If
"row", reshuffling is performed with respect to row-wise vectorization. If"column", reshuffling is performed with respect to column-wise vectorization. If"system", operator is converted to a representation based on row vectorization, reshuffled, and then converted back to its representation with respect to system-wise vectorization. Defaults to"row".precision_tol (float, optional) – Precision tolerance for eigenvalues found in the spectral decomposition problem. Any eigenvalue \(\lambda <\)
precision_tolis set to 0 (zero). IfNone,precision_toldefaults toqibo.config.PRECISION_TOL=1e-8. Defaults toNone.validate_cp (bool, optional) – If
True, checks ifchoi_super_opis a completely positive map. IfFalse, it assumes thatchoi_super_opis completely positive (and Hermitian). Defaults toTrue.nqubits (int, optional) – total number of qubits in the system that is interacting with the environment. Must be equal or greater than the number of qubits
kraus_opsacts on. IfNone, defaults to the number of qubits inkraus_ops. Defauts toNone.initial_state_env (ndarray, optional) – statevector representing the initial state of the enviroment. If
None, it assumes the environment in its ground state. Defaults toNone.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Stinespring representation of quantum channel.
- Return type:
ndarray
Pauli-Liouville to Liouville#
- qibo.quantum_info.pauli_to_liouville(pauli_op, normalize: bool = False, order: str = 'row', pauli_order: str = 'IXYZ', backend=None)[source]#
Converts Pauli-Liouville representation of a quantum channel to its Liouville representation \(\mathcal{E}\).
- Parameters:
pauli_op (ndarray) – Pauli-Liouville representation of a quantum channel.
normalize (bool, optional) – If
Trueassumespauli_opis represented in the normalized Pauli basis. IfFalse, it assumes unnormalized Pauli basis. Defaults toFalse.order (str, optional) – If
"row", returns Liouville representation in row-vectorization. If"column", returns column-vectorized superoperator. If"system", superoperator will be in block-vectorization. Defaults to"row".pauli_order (str, optional) – corresponds to the order of 4 single-qubit Pauli elements. Defaults to “IXYZ”.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
superoperator in the Liouville representation.
- Return type:
ndarray
Pauli-Liouville to Choi#
- qibo.quantum_info.pauli_to_choi(pauli_op, normalize: bool = False, order: str = 'row', pauli_order: str = 'IXYZ', backend=None)[source]#
Converts Pauli-Liouville representation of a quantum channel to its Choi representation \(\Lambda\).
- Parameters:
pauli_op (ndarray) – superoperator in the Pauli-Liouville representation.
normalize (bool, optional) – If
Trueassumespauli_opis represented in the normalized Pauli basis. IfFalse, it assumes unnormalized Pauli basis. Defaults toFalse.order (str, optional) – If
"row", returns Choi representation in row-vectorization. If"column", returns column-vectorized superoperator. Defaults to"row".pauli_order (str, optional) – corresponds to the order of 4 single-qubit Pauli elements. Defaults to “IXYZ”.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Choi representation of the superoperator.
- Return type:
ndarray
Pauli-Liouville to Kraus#
- qibo.quantum_info.pauli_to_kraus(pauli_op, normalize: bool = False, order: str = 'row', pauli_order: str = 'IXYZ', precision_tol: float | None = None, backend=None)[source]#
Converts Pauli-Liouville representation of a quantum channel to its Kraus representation \(\{K_{\alpha}\}_{\alpha}\).
- Parameters:
pauli_op (ndarray) – superoperator in the Pauli-Liouville representation.
normalize (bool, optional) – If
Trueassumespauli_opis represented in the normalized Pauli basis. IfFalse, it assumes unnormalized Pauli basis. Defaults toFalse.order (str, optional) – vectorization order of the Liouville and Choi intermediate steps. If
"row", row-vectorizationcis used for both representations. If"column", column-vectorization is used. Defaults to"row".pauli_order (str, optional) – corresponds to the order of 4 single-qubit Pauli elements. Defaults to “IXYZ”.
precision_tol (float, optional) – Precision tolerance for eigenvalues found in the spectral decomposition problem. Any eigenvalue \(\lambda <\)
precision_tolis set to 0 (zero). IfNone,precision_toldefaults toqibo.config.PRECISION_TOL=1e-8. Defaults toNone.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Kraus operators and their coefficients.
- Return type:
(ndarray, ndarray)
Pauli-Liouville to Chi-matrix#
- qibo.quantum_info.pauli_to_chi(pauli_op, normalize: bool = False, order: str = 'row', pauli_order: str = 'IXYZ', backend=None)[source]#
Converts Pauli-Liouville representation of a quantum channel to its \(\chi\)-matrix representation.
- Parameters:
pauli_op (ndarray) – superoperator in the Pauli-Liouville representation.
normalize (bool, optional) – If
Trueassumespauli_opis represented in the normalized Pauli basis. IfFalse, it assumes unnormalized Pauli basis. Defaults toFalse.order (str, optional) – If
"row", returns Choi representation in row-vectorization. If"column", returns column-vectorized superoperator. Defaults to"row".pauli_order (str, optional) – corresponds to the order of 4 single-qubit Pauli elements. Defaults to “IXYZ”.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Chi-matrix representation of the quantum channel.
- Return type:
ndarray
Pauli-Liouville to Stinespring#
- qibo.quantum_info.pauli_to_stinespring(pauli_op, normalize: bool = False, order: str = 'row', pauli_order: str = 'IXYZ', precision_tol: float | None = None, validate_cp: bool = True, nqubits: int | None = None, initial_state_env=None, backend=None)[source]#
Converts Pauli-Liouville representation \(\mathcal{E}_{P}\) of quantum channel to its Stinespring representation \(U_{0}\). It uses the Liouville representation \(\mathcal{E}\) as intermediate step.
- Parameters:
pauli_op (ndarray) – Pauli-Liouville representation of a quantum channel.
normalize (bool, optional) – If
Trueassumespauli_opis represented in the normalized Pauli basis. IfFalse, it assumes unnormalized Pauli basis. Defaults toFalse.order (str, optional) – If
"row", returns Liouville representation in row-vectorization. If"column", returns column-vectorized superoperator. If"system", superoperator will be in block-vectorization. Defaults to"row".pauli_order (str, optional) – corresponds to the order of 4 single-qubit Pauli elements. Defaults to “IXYZ”.
precision_tol (float, optional) – Precision tolerance for eigenvalues found in the spectral decomposition problem. Any eigenvalue \(\lambda <\)
precision_tolis set to 0 (zero). IfNone,precision_toldefaults toqibo.config.PRECISION_TOL=1e-8. Defaults toNone.validate_cp (bool, optional) – If
True, checks ifchoi_super_opis a completely positive map. IfFalse, it assumes thatchoi_super_opis completely positive (and Hermitian). Defaults toTrue.nqubits (int, optional) – total number of qubits in the system that is interacting with the environment. Must be equal or greater than the number of qubits
kraus_opsacts on. IfNone, defaults to the number of qubits inkraus_ops. Defauts toNone.initial_state_env (ndarray, optional) – statevector representing the initial state of the enviroment. If
None, it assumes the environment in its ground state. Defaults toNone.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Stinestring representation of quantum channel.
- Return type:
ndarray
Chi-matrix to Choi#
- qibo.quantum_info.chi_to_choi(chi_matrix, normalize: bool = False, order: str = 'row', pauli_order: str = 'IXYZ', backend=None)[source]#
Convert the \(\chi\)-matrix representation of a quantum channel to its Choi representation \(\Lambda\).
\[\Lambda = \text{pauli_to_liouville}(\chi)\]- Parameters:
chi_matrix – Chi-matrix representation of quantum channel.
normalize (bool, optional) – If
Trueassumes the normalized Pauli basis. IfFalse, it assumes unnormalized Pauli basis. Defaults toFalse.order (str, optional) – If
"row", reshuffling is performed with respect to row-wise vectorization. If"column", reshuffling is performed with respect to column-wise vectorization. If"system", operator is converted to a representation based on row vectorization, reshuffled, and then converted back to its representation with respect to system-wise vectorization. Defaults to"row".pauli_order (str, optional) – corresponds to the order of 4 single-qubit Pauli elements. Defaults to “IXYZ”.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Choi representation of quantum channel.
- Return type:
ndarray
Chi-matrix to Liouville#
- qibo.quantum_info.chi_to_liouville(chi_matrix, normalize: bool = False, order: str = 'row', pauli_order: str = 'IXYZ', backend=None)[source]#
Converts the \(\chi\)-matrix representation of a quantum channel to its Liouville representation \(\mathcal{E}\).
\[\mathcal{E} = \text{pauli_to_liouville}(\text{choi_to_liouville}(\chi))\]- Parameters:
chi_matrix – Chi-matrix representation of quantum channel.
normalize (bool, optional) – If
Trueassumes the normalized Pauli basis. IfFalse, it assumes unnormalized Pauli basis. Defaults toFalse.order (str, optional) – If
"row", reshuffling is performed with respect to row-wise vectorization. If"column", reshuffling is performed with respect to column-wise vectorization. If"system", operator is converted to a representation based on row vectorization, reshuffled, and then converted back to its representation with respect to system-wise vectorization. Defaults to"row".pauli_order (str, optional) – corresponds to the order of 4 single-qubit Pauli elements. Defaults to “IXYZ”.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Liouville representation of quantum channel.
- Return type:
ndarray
Chi-matrix to Pauli-Liouville#
- qibo.quantum_info.chi_to_pauli(chi_matrix, normalize: bool = False, order: str = 'row', pauli_order: str = 'IXYZ', backend=None)[source]#
Convert \(\chi\)-matrix representation of a quantum channel to its Pauli-Liouville representation \(\mathcal{E}_P\).
\[\mathcal{E}_P = \text{choi_to_pauli}(\text{chi_to_choi}(\chi))\]- Parameters:
chi_matrix – Chi-matrix representation of quantum channel.
normalize (bool, optional) – If
Trueassumes the normalized Pauli basis. IfFalse, it assumes unnormalized Pauli basis. Defaults toFalse.order (str, optional) – If
"row", reshuffling is performed with respect to row-wise vectorization. If"column", reshuffling is performed with respect to column-wise vectorization. If"system", operator is converted to a representation based on row vectorization, reshuffled, and then converted back to its representation with respect to system-wise vectorization. Defaults to"row".pauli_order (str, optional) – corresponds to the order of 4 single-qubit Pauli elements. Defaults to “IXYZ”.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
superoperator in the Pauli-Liouville representation.
- Return type:
ndarray
Chi-matrix to Kraus#
- qibo.quantum_info.chi_to_kraus(chi_matrix, normalize: bool = False, precision_tol: float | None = None, order: str = 'row', pauli_order: str = 'IXYZ', validate_cp: bool = True, backend=None)[source]#
Converts the \(\chi\)-matrix representation of a quantum channel to its Kraus representation \(\{K_{\alpha}\}_{\alpha}\).
\[\mathcal{E}_P = \text{choi_to_kraus}(\text{chi_to_choi}(\chi))\]- Parameters:
chi_matrix – Chi-matrix representation of quantum channel.
normalize (bool, optional) – If
Trueassumes the normalized Pauli basis. IfFalse, it assumes unnormalized Pauli basis. Defaults toFalse.precision_tol (float, optional) – Precision tolerance for eigenvalues found in the spectral decomposition problem. Any eigenvalue \(\lambda <\)
precision_tolis set to 0 (zero). IfNone,precision_toldefaults toqibo.config.PRECISION_TOL=1e-8. Defaults toNone.order (str, optional) – If
"row", reshuffling is performed with respect to row-wise vectorization. If"column", reshuffling is performed with respect to column-wise vectorization. If"system", operator is converted to a representation based on row vectorization, reshuffled, and then converted back to its representation with respect to system-wise vectorization. Defaults to"row".pauli_order (str, optional) – corresponds to the order of 4 single-qubit Pauli elements. Defaults to “IXYZ”.
validate_cp (bool, optional) – If
True, checks ifchoi_super_opis a completely positive map. IfFalse, it assumes thatchoi_super_opis completely positive (and Hermitian). Defaults toTrue.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Kraus operators and their coefficients.
- Return type:
(ndarray, ndarray)
Note
Due to the spectral decomposition subroutine in this function, the resulting Kraus operators \(\{K_{\alpha}\}_{\alpha}\) might contain global phases. That implies these operators are not exactly equal to the “true” Kraus operators \(\{K_{\alpha}^{(\text{ideal})}\}_{\alpha}\). However, since these are global phases, the operators’ actions are the same, i.e.
Note
User can set validate_cp=False in order to speed up execution by not checking if
the Choi representation obtained from the input chi_matrix is completely positive
(CP) and Hermitian. However, that may lead to erroneous outputs if choi_super_op
is not guaranteed to be CP. We advise users to either set this flag carefully or leave
it in its default setting (validate_cp=True).
Chi-matrix to Stinespring#
- qibo.quantum_info.chi_to_stinespring(chi_matrix, normalize: bool = False, order: str = 'row', pauli_order: str = 'IXYZ', precision_tol: float | None = None, validate_cp: bool = True, nqubits: int | None = None, initial_state_env=None, backend=None)[source]#
Converts \(\chi\)-representation of quantum channel to its Stinespring representation \(U_{0}\). It uses the Choi representation \(\Lambda\) as intermediate step.
- Parameters:
chi_matrix – Chi-matrix representation of quantum channel.
normalize (bool, optional) – If
Trueassumes the normalized Pauli basis. IfFalse, it assumes unnormalized Pauli basis. Defaults toFalse.order (str, optional) – If
"row", reshuffling is performed with respect to row-wise vectorization. If"column", reshuffling is performed with respect to column-wise vectorization. If"system", operator is converted to a representation based on row vectorization, reshuffled, and then converted back to its representation with respect to system-wise vectorization. Defaults to"row".pauli_order (str, optional) – corresponds to the order of 4 single-qubit Pauli elements. Defaults to “IXYZ”.
precision_tol (float, optional) – Precision tolerance for eigenvalues found in the spectral decomposition problem. Any eigenvalue \(\lambda <\)
precision_tolis set to 0 (zero). IfNone,precision_toldefaults toqibo.config.PRECISION_TOL=1e-8. Defaults toNone.order – If
"row", reshuffling is performed with respect to row-wise vectorization. If"column", reshuffling is performed with respect to column-wise vectorization. If"system", operator is converted to a representation based on row vectorization, reshuffled, and then converted back to its representation with respect to system-wise vectorization. Defaults to"row".validate_cp (bool, optional) – If
True, checks ifchoi_super_opis a completely positive map. IfFalse, it assumes thatchoi_super_opis completely positive (and Hermitian). Defaults toTrue.nqubits (int, optional) – total number of qubits in the system that is interacting with the environment. Must be equal or greater than the number of qubits
kraus_opsacts on. IfNone, defaults to the number of qubits inkraus_ops. Defauts toNone.initial_state_env (ndarray, optional) – statevector representing the initial state of the enviroment. If
None, it assumes the environment in its ground state. Defaults toNone.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Stinespring representation of quantum channel.
- Return type:
ndarray
Stinespring to Choi#
- qibo.quantum_info.stinespring_to_choi(stinespring, dim_env: int, initial_state_env=None, nqubits: int | None = None, order: str = 'row', backend=None)[source]#
Converts Stinespring representation \(U_{0}\) of quantum channel to its Choi representation \(\Lambda\).
\[\Lambda = \text{kraus_to_choi}(\text{stinespring_to_kraus}(U_{0}))\]- Parameters:
stinespring (ndarray) – quantum channel in the Stinespring representation.
dim_env (int) – dimension of the Hilbert space of the environment.
initial_state_env (ndarray, optional) – statevector representing the initial state of the enviroment. If
None, it assumes the environment in its ground state. Defaults toNone.nqubits (int, optional) – number of qubits in the system. Defaults to
None.order (str, optional) – If
"row", reshuffling is performed with respect to row-wise vectorization. If"column", reshuffling is performed with respect to column-wise vectorization. If"system", operator is converted to a representation based on row vectorization, reshuffled, and then converted back to its representation with respect to system-wise vectorization. Defaults to"row".backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Choi representation of quantum channel.
- Return type:
ndarray
Stinespring to Liouville#
- qibo.quantum_info.stinespring_to_liouville(stinespring, dim_env: int, initial_state_env=None, nqubits: int | None = None, order: str = 'row', backend=None)[source]#
Converts Stinespring representation \(U_{0}\) of quantum channel to its Liouville representation \(\mathcal{E}\) via Stinespring Dilation, i.e.
\[\mathcal{E} = \text{kraus_to_liouville}(\text{stinespring_to_kraus}(U_{0}))\]- Parameters:
stinespring (ndarray) – quantum channel in the Stinespring representation.
dim_env (int) – dimension of the Hilbert space of the environment.
initial_state_env (ndarray, optional) – statevector representing the initial state of the enviroment. If
None, it assumes the environment in its ground state. Defaults toNone.nqubits (int, optional) – number of qubits in the system. Defaults to
None.order (str, optional) – If
"row", reshuffling is performed with respect to row-wise vectorization. If"column", reshuffling is performed with respect to column-wise vectorization. If"system", operator is converted to a representation based on row vectorization, reshuffled, and then converted back to its representation with respect to system-wise vectorization. Defaults to"row".backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Liouville representation of quantum channel.
- Return type:
ndarray
Stinespring to Pauli-Liouville#
- qibo.quantum_info.stinespring_to_pauli(stinespring, dim_env: int, initial_state_env=None, nqubits: int | None = None, normalize: bool = False, order: str = 'row', pauli_order: str = 'IXYZ', backend=None)[source]#
Converts Stinespring representation \(U_{0}\) of quantum channel to its Pauli-Liouville representation \(\mathcal{E}_{P}\) via Stinespring Dilation, i.e.
\[\mathcal{E}_{P} = \text{kraus_to_pauli}(\text{stinespring_to_kraus}(U_{0}))\]- Parameters:
stinespring (ndarray) – quantum channel in the Stinespring representation.
dim_env (int) – dimension of the Hilbert space of the environment.
initial_state_env (ndarray, optional) – statevector representing the initial state of the enviroment. If
None, it assumes the environment in its ground state. Defaults toNone.nqubits (int, optional) – number of qubits in the system. Defaults to
None.normalize (bool, optional) – If
Truesuperoperator is returned in the normalized Pauli basis. IfFalse, it is returned in the unnormalized Pauli basis. Defaults toFalse.order (str, optional) – If
"row", intermediate step for Choi representation is done in row-vectorization. If"column", step is done in column-vectorization. If"system", block-vectorization is performed. Defaults to"row".pauli_order (str, optional) – corresponds to the order of 4 single-qubit Pauli elements. Defaults to “IXYZ”.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Pauli-Liouville representation of quantum channel.
- Return type:
ndarray
Stinespring to Kraus#
- qibo.quantum_info.stinespring_to_kraus(stinespring, dim_env: int, initial_state_env=None, nqubits: int | None = None, backend=None)[source]#
Converts the Stinespring representation \(U_{0}\) of quantum channel to its Kraus representation \(\{K_{\alpha}\}_{\alpha}\), i.e.
\[K_{\alpha} := \bra{\alpha} \, U_{0} \, \ket{v_{0}} \, ,\]where \(\ket{v_{0}}\) is the initial state of the environment (
initial_state_env), \(D\) is the dimension of the environment’s Hilbert space, and \(\{\ket{\alpha} \, : \, \alpha = 0, 1, \cdots, D - 1 \}\) is an orthonormal basis for the environment’s Hilbert space. Note that \(\text{dim}(\ket{\alpha}) = \text{dim}(\ket{v_{0}}) = D\), while \(\text{dim}(U) = 2^{n} \, D\), where \(n\) is nqubits.- Parameters:
stinespring (ndarray) – quantum channel in the Stinespring representation.
dim_env (int) – dimension of the Hilbert space of the environment.
initial_state_env (ndarray, optional) – statevector representing the initial state of the enviroment. If
None, it assumes the environment in its ground state. Defaults toNone.nqubits (int, optional) – number of qubits in the system. Defaults to
None.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Kraus operators.
- Return type:
ndarray
Stinespring to Chi-matrix#
- qibo.quantum_info.stinespring_to_chi(stinespring, dim_env: int, initial_state_env=None, nqubits: int | None = None, normalize: bool = False, order: str = 'row', pauli_order: str = 'IXYZ', backend=None)[source]#
Converts Stinespring representation \(U_{0}\) of quantum channel to its \(\chi\)-matrix representation via Stinespring Dilation, i.e.
\[\chi = \text{kraus_to_chi}(\text{stinespring_to_kraus}(U_{0}))\]- Parameters:
stinespring (ndarray) – quantum channel in the Stinespring representation.
dim_env (int) – dimension of the Hilbert space of the environment.
initial_state_env (ndarray, optional) – statevector representing the initial state of the enviroment. If
None, it assumes the environment in its ground state. Defaults toNone.nqubits (int, optional) – number of qubits in the system. Defaults to
None.normalize (bool, optional) – If
Trueassumes the normalized Pauli basis. IfFalse, it assumes unnormalized Pauli basis. Defaults toFalse.order (str, optional) – If
"row", reshuffling is performed with respect to row-wise vectorization. If"column", reshuffling is performed with respect to column-wise vectorization. If"system", operator is converted to a representation based on row vectorization, reshuffled, and then converted back to its representation with respect to system-wise vectorization. Defaults to"row".pauli_order (str, optional) – corresponds to the order of 4 single-qubit Pauli elements in the Pauli basis. Defaults to “IXYZ”.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
\(\chi\)-representation of quantum channel.
- Return type:
ndarray
Kraus operators as probabilistic sum of unitaries#
- qibo.quantum_info.kraus_to_unitaries(kraus_ops, order: str = 'row', precision_tol: float | None = None, backend=None)[source]#
Tries to convert Kraus operators into a probabilistc sum of unitaries.
Given a set of Kraus operators \(\{K_{\alpha}\}_{\alpha}\), returns an ensemble \(\{U_{\alpha}, p_{\alpha}\}\) that defines an
qibo.gates.channels.UnitaryChannelthat approximates the original channel up to a precision tolerance in Frobenius norm.- Parameters:
kraus_ops (list) – List of Kraus operators as pairs
(qubits, Ak)wherequbitsrefers the qubit ids that \(A_k\) acts on and \(A_k\) is the corresponding matrix as anp.ndarray.order (str, optional) – _description_. Defaults to “row”.
precision_tol (float, optional) – Precision tolerance for the minimization of the Frobenius norm \(\| \mathcal{E}_{K} - \mathcal{E}_{U} \|_{F}\), where \(\mathcal{E}_{K}\) is the Liouville representation of the Kraus channel \(\{K_{\alpha}\}_{\alpha}\), and \(\mathcal{E}_{U}\) is the Liouville representaton of the
qibo.gates.channels.UnitaryChannelthat best approximates the original channel. IfNone,precision_toldefaults to1e-7. Defaults toNone.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Unitary operators and their associated probabilities.
- Return type:
(ndarray, ndarray)
Note
It is not guaranteed that a good approximation will be found or that any approximation will be found at all. This functions will find good solutions for a limited set of operators. We leave to the user to decide how to best use this function.
Utility Functions#
Functions that can be used to calculate metrics and distance measures on classical probability arrays.
Hamming weight#
- qibo.quantum_info.hamming_weight(bitstring: int | str | list | tuple, return_indexes: bool = False)[source]#
Calculates the Hamming weight of a bitstring.
The Hamming weight of a bistring is the number of :math:’1’s that the bistring contains.
- Parameters:
- Returns:
Hamming weight of bitstring or list of indexes of non-zero elements.
- Return type:
Hamming distance#
- qibo.quantum_info.hamming_distance(bitstring_1: int | str | list | tuple, bitstring_2: int | str | list | tuple, return_indexes: bool = False)[source]#
Calculates the Hamming distance between two bistrings.
This is done by calculating the Hamming weight (
qibo.quantum_info.utils.hamming_weight()) of| bitstring_1 - bitstring_2 |.- Parameters:
- Returns:
Hamming distance or list of indexes of non-zero elements.
- Return type:
Hadamard Transform#
- qibo.quantum_info.hadamard_transform(array, implementation: str = 'fast', backend=None)[source]#
Calculates the (fast) Hadamard Transform \(\text{HT}\) of a \(2^{n}\)-dimensional vector or \(2^{n} \times 2^{n}\) matrix \(A\), where \(n\) is the number of qubits in the system. If \(A\) is a vector, then
\[\text{HT}(A) = \frac{1}{2^{n / 2}} \, H^{\otimes n} \, A \,\]where \(H\) is the
qibo.gates.Hgate. If \(A\) is a matrix, then\[\text{HT}(A) = \frac{1}{2^{n}} \, H^{\otimes n} \, A \, H^{\otimes n} \, .\]- Parameters:
array (ndarray) – array or matrix.
implementation (str, optional) – if
"regular", it uses the straightforward implementation of the algorithm with computational complexity of \(\mathcal{O}(2^{2n})\) for vectors and \(\mathcal{O}(2^{3n})\) for matrices. If"fast", computational complexity is \(\mathcal{O}(n \, 2^{n})\) in both cases.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
(Fast) Hadamard Transform of
array.- Return type:
ndarray
Hellinger distance#
- qibo.quantum_info.hellinger_distance(prob_dist_p, prob_dist_q, validate: bool = False, backend=None)[source]#
Calculates the Hellinger distance \(H\) between two discrete probability distributions.
For probabilities \(\mathbf{p}\) and \(\mathbf{q}\), it is defined as
\[H(\mathbf{p} \, , \, \mathbf{q}) = \frac{1}{\sqrt{2}} \, \| \sqrt{\mathbf{p}} - \sqrt{\mathbf{q}} \|_{2}\]where \(\|\cdot\|_{2}\) is the Euclidean norm.
- Parameters:
prob_dist_p (ndarray or list) – discrete probability distribution \(p\).
prob_dist_q (ndarray or list) – discrete probability distribution \(q\).
validate (bool, optional) – If
True, checks if \(p\) and \(q\) are proper probability distributions. Defaults toFalse.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Hellinger distance \(H(p, q)\).
- Return type:
(float)
Hellinger fidelity#
- qibo.quantum_info.hellinger_fidelity(prob_dist_p, prob_dist_q, validate: bool = False, backend=None)[source]#
Calculates the Hellinger fidelity between two discrete probability distributions.
For probabilities \(p\) and \(q\), the fidelity is defined as
\[(1 - H^{2}(p, q))^{2} \, ,\]where \(H(p, q)\) is the
qibo.quantum_info.hellinger_distance().- Parameters:
prob_dist_p (ndarray or list) – discrete probability distribution \(p\).
prob_dist_q (ndarray or list) – discrete probability distribution \(q\).
validate (bool, optional) – if
True, checks if \(p\) and \(q\) are proper probability distributions. Defaults toFalse.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Hellinger fidelity.
- Return type:
Hellinger shot error#
- qibo.quantum_info.hellinger_shot_error(prob_dist_p, prob_dist_q, nshots: int, validate: bool = False, backend=None)[source]#
Calculates the Hellinger fidelity error between two discrete probability distributions estimated from finite statistics.
It is calculated propagating the probability error of each state of the system. The complete formula is:
\[\frac{1 - H^{2}(p, q)}{\sqrt{nshots}} \, \sum_{k} \, \left(\sqrt{p_{k} \, (1 - q_{k})} + \sqrt{q_{k} \, (1 - p_{k})}\right)\]where \(H(p, q)\) is the
qibo.quantum_info.hellinger_distance(), and \(1 - H^{2}(p, q)\) is the square root of theqibo.quantum_info.hellinger_fidelity().- Parameters:
prob_dist_p (ndarray or list) – discrete probability distribution \(p\).
prob_dist_q (ndarray or list) – discrete probability distribution \(q\).
nshots (int) – number of shots we used to run the circuit to obtain \(p\) and \(q\).
validate (bool, optional) – if
True, checks if \(p\) and \(q\) are proper probability distributions. Defaults toFalse.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Hellinger fidelity error.
- Return type:
Total variation distance#
- qibo.quantum_info.total_variation_distance(prob_dist_p, prob_dist_q, validate: bool = False, backend=None)[source]#
Calculate the total variation distance between two discrete probability distributions.
For probabilities \(p\) and \(q\), the total variation distance is defined as
\[\operatorname{TVD}(p, \, q) = \frac{1}{2} \, \|p - q\|_{1} = \frac{1}{2} \, \sum_{x} \, \left|p(x) - q(x)\right| \, ,\]where \(\|\cdot\|_{1}\) detones the \(\ell_{1}\)-norm.
- Parameters:
prob_dist_p (ndarray or list) – discrete probability distribution \(p\).
prob_dist_q (ndarray or list) – discrete probability distribution \(q\).
validate (bool, optional) – if
True, checks if \(p\) and \(q\) are proper probability distributions. Defaults toFalse.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Total variation distance measure.
- Return type:
Haar integral#
- qibo.quantum_info.haar_integral(nqubits: int, power_t: int, samples: int | None = None, backend=None)[source]#
Returns the integral over pure states over the Haar measure.
\[\int_{\text{Haar}} d\psi \, \left(|\psi\rangle\right.\left. \langle\psi|\right)^{\otimes t}\]- Parameters:
nqubits (int) – Number of qubits.
power_t (int) – power that defines the \(t\)-design.
samples (int, optional) – If
None, estimated the integral exactly. Otherwise, number of samples to estimate the integral via sampling. Defaults toNone.backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Estimation of the Haar integral.
- Return type:
array
Note
The
exact=Truemethod is implemented using Lemma 34 of Kliesch and Roth (2020).
Parameterized quantum circuit integral#
- qibo.quantum_info.pqc_integral(circuit, power_t: int, samples: int, backend=None)[source]#
Returns the integral over pure states generated by uniformly sampling in the parameter space described by a parameterized circuit.
\[\int_{\Theta} d\psi \, \left(|\psi_{\theta}\rangle\right.\left. \langle\psi_{\theta}|\right)^{\otimes t}\]- Parameters:
circuit (
qibo.models.Circuit) – Parametrized circuit.power_t (int) – power that defines the \(t\)-design.
samples (int) – number of samples to estimate the integral.
backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
Estimation of the integral.
- Return type:
ndarray
Decompose permutation into the fewest pairwise transpositions#
- qibo.quantum_info.decompose_permutation(sigma: List[int] | Tuple[int, ...], m: int, backend=None)[source]#
Given permutation
sigmaon \(\{0, \, 1, \, \dots, \, d-1\}\)and a power‑of‑two budget
m, this function factorssigmainto the fewest layers \(\sigma_{1}, \, \sigma_{2}, \, \cdots, \, \sigma_{t}\) such that:each layer has at most \(m\) disjoint transpositions
each layer moves a power‑of‑two number of indices.
- We do this as follows:
Cycle extraction – split sigma into disjoint cycles.
Star factorisation – a k‑cycle becomes (k-1) hub–spoke swaps.
Greedy packing – merge swaps into layers while keeping rules.
- Parameters:
- Returns:
\(t\) layers of pairwise transpositions.
- Return type:
Tomography#
Functions used to classically simulate tomography protocols.
Gate Set Tomography#
Gate Set Tomography (GST) is a powerful technique employed in quantum information processing to characterize the behavior of quantum gates on quantum hardware [1, 2, 3]. The primary objective of GST is to provide a robust framework for obtaining a representation of quantum gates within a predefined gate set when subjected to noise inherent to the quantum hardware.
By characterizing the impact of noise on quantum gates, GST enables the identification and quantification of errors, laying the groundwork for subsequent error mitigation strategies. The insights gained from GST are instrumental, for instance, in setting up the necessary parameters for Probabilistic Error Cancellation (PEC).
In practice, given a set of operators (or gates), \(\mathcal{O}=\{O_0, O_1, \dots, O_n\}\), a set of initial states \(\{\rho_k\}\), and a set of measurement bases \(\{M_j\}\), one performs GST on the \(l\)-th operator by choosing an initial state \(\rho_k\), applying the gate \(O_l \in \mathcal{O}\), measuring in the \(M_j\) basis in order to obtain the following matrix:
which provides an estimated representation of the operator \(O_l\) in the specific system.
This implementation makes use, in particular, of \(\rho_k \in \{ \ketbra{0}{0}, \ketbra{1}{1}, \ketbra{+}{+}, \ketbra{y+}{y+} \}^{\otimes n}\) and \(M_j \in \{ I, X, Y, Z\}^{\otimes n}\) [4], with \(n\in\{1,2\}\) being the number of qubits. However, \(\{\tilde{O}_l\}_{jk}\) is not yet given in the Pauli-Liouville representation (also known as Pauli Transfer Matrix). To obtain the Pauli-Liouville representation, one needs the two matrices, described below. The matrix \(\tilde{g}\) has its elements \(\tilde{g}_{jk}\) defined as
which is obtained by measuring the initial states \(\{\rho_k\}\) in each basis element \(\{M_j\}\) without any gates’ application. The gauge matrix \(T\) is given by
This is the matrix, in a common gauge, implementing a change of basis. Therefore, the Pauli-Liouville representation can be recovered as
- References:
1. R. Blume-Kohout et al. Robust, self-consistent, closed-form tomography of quantum logic gates on a trapped ion qubit (2013), arXiv:1310.4492.
2. D. Greenbaum, Introduction to quantum gate set tomography (2015), arXiv:1509.02921.
3. E. Nielsen et al., Gate set tomography (2021), Quantum 5, 557.
4. S. Endo, S. C. Benjamin, and Y. Li, Practical quantum error mitigation for near-future applications (2018), Physical Review X 8.3: 031027.
- qibo.tomography.gate_set_tomography.GST(gate_set: tuple | set | list, nshots=10000, noise_model=None, include_empty=False, pauli_liouville=False, gauge_matrix=None, backend=None, transpiler=None)[source]#
Run Gate Set Tomography on the input
gate_set.- Parameters:
gate_set (tuple or set or list) – set of
qibo.gates.Gateand parameters to run GST on. For instance,gate_set = [(gates.RX, [np.pi/3]), gates.Z, (gates.PRX, [np.pi/2, np.pi/3]), (gates.GPI, [np.pi/7]), gates.CNOT].nshots (int, optional) – number of shots used in Gate Set Tomography per gate. Defaults to \(10^{4}\).
noise_model (
qibo.noise.NoiseModel, optional) – noise model applied to simulate noisy computations.include_empty (bool, optional) – if
True, additionally performs gate set tomography for \(1\)- and \(2\)-qubit empty circuits, returning the corresponding empty matrices in the first and second position of the ouput list.pauli_liouville (bool, optional) – if
True, returns the matrices in the Pauli-Liouville representation. Defaults toFalse.gauge_matrix (ndarray, optional) –
gauge matrix transformation to the Pauli-Liouville representation. Defaults to
\[\begin{split}\begin{pmatrix} 1 & 1 & 1 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & -1 & 0 & 0 \\ \end{pmatrix}\end{split}\]backend (
qibo.backends.abstract.Backend, optional) – backend to be used in the execution. IfNone, it uses the current backend. Defaults toNone.
- Returns:
input
gate_setrepresented by matrices estimaded via GST.- Return type:
List(ndarray)
Parallelism#
We provide CPU multi-processing methods for circuit evaluation for multiple input states and multiple parameters for fixed input state.
When using the methods below the processes option controls the number of
processes used by the parallel algorithms through the multiprocessing
library. By default processes=None, in this case the total number of logical
cores are used. Make sure to select the appropriate number of processes for your
computer specification, taking in consideration memory and physical cores. In
order to obtain optimal results you can control the number of threads used by
each process with the qibo.set_threads method. For example, for small-medium
size circuits you may benefit from single thread per process, thus set
qibo.set_threads(1) before running the optimization.
Resources for parallel circuit evaluation.
- qibo.parallel.parallel_execution(circuit, states, processes: int | None = None, backend=None)[source]#
Execute circuit for multiple states.
Example
import qibo qibo.set_backend('qibojit') from qibo import models, set_threads from qibo.parallel import parallel_execution import numpy as np # create circuit nqubits = 22 circuit = models.QFT(nqubits) # create random states states = [ np.random.random(2**nqubits) for i in range(5)] # set threads to 1 per process (optional, requires tuning) set_threads(1) # execute in parallel results = parallel_execution(circuit, states, processes=2)
- qibo.parallel.parallel_circuits_execution(circuits, states=None, nshots=1000, processes=None, backend=None)[source]#
Execute multiple circuits
Example
import qibo qibo.set_backend('qibojit') from qibo import models, set_threads from qibo.parallel import parallel_circuits_execution import numpy as np # create different circuits circuits = [models.QFT(n) for n in range(5, 16)] # set threads to 1 per process (optional, requires tuning) set_threads(1) # execute in parallel results = parallel_circuits_execution(circuits, processes=2)
- Parameters:
circuits (list) – list of circuits to execute.
states (optional, list) – list of states to use as initial for each circuit. Must have the same length as
circuits. If one state is given it is used on all circuits. If not given the default initial state on all circuits.nshots (int) – Number of shots when performing measurements, same for all circuits.
processes (int) – number of processes for parallel evaluation.
- Returns:
Circuit evaluation for input states.
- qibo.parallel.parallel_parametrized_execution(circuit, parameters, initial_state=None, processes: int | None = None, backend=None)[source]#
Execute circuit for multiple parameters and fixed initial_state.
Example
import numpy as np from qibo import Circuit, gates, set_backend, set_threads from qibo.parallel import parallel_parametrized_execution set_backend('qibojit') # create circuit nqubits = 6 nlayers = 2 circuit = Circuit(nqubits) for l in range(nlayers): circuit.add((gates.RY(q, theta=0) for q in range(nqubits))) circuit.add((gates.CZ(q, q+1) for q in range(0, nqubits-1, 2))) circuit.add((gates.RY(q, theta=0) for q in range(nqubits))) circuit.add((gates.CZ(q, q+1) for q in range(1, nqubits-2, 2))) circuit.add(gates.CZ(0, nqubits-1)) circuit.add((gates.RY(q, theta=0) for q in range(nqubits))) # create random parameters size = len(circuit.get_parameters()) parameters = [ np.random.uniform(0, 2*np.pi, size) for _ in range(10) ] # set threads to 1 per process (optional, requires tuning) set_threads(1) # execute in parallel results = parallel_parametrized_execution(circuit, parameters, processes=2)
- Parameters:
circuit (
qibo.models.Circuit) – the input circuit.parameters (list) – list of parameters for the circuit evaluation.
initial_state (ndarray) – initial state for the circuit evaluation.
processes (int) – number of processes for parallel evaluation. This corresponds to the number of threads, if a single thread is used for each circuit evaluation. If more threads are used for each circuit evaluation then some tuning may be required to obtain optimal performance. Default is
Nonewhich corresponds to a single thread.
- Returns:
Circuit evaluation for input parameters.
Backends#
qibo.backends.abstract.Backend is the main calculation engine to execute circuits.
Qibo provides backends for quantum simulation on classical hardware, as well as quantum hardware management and control.
For a complete list of available backends, refer to the Packages section.
To create new backends, inherit from qibo.backends.abstract.Backend and implement
its abstract methods. This abstract class defines the required methods for circuit execution.
The user can set the backend using the qibo.set_backend() function.
import qibo
qibo.set_backend("qibojit")
# Switch to the numpy backend
qibo.set_backend("numpy")
If no backend is specified, the default backend is used.
The default backend is selected in the following order: qibojit, numpy, and qiboml.
The list of default backend candidates can be changed using the QIBO_BACKEND environment variable.
Some backends support different platforms. For example, the qibojit backend
provides two platforms (cupy and cuquantum) when used on GPU.
The platform can be specified using the platform parameter in the qibo.set_backend() function.
import qibo
qibo.set_backend("qibojit", platform="cuquantum")
# Switch to the cupy platform
qibo.set_backend("qibojit", platform="cupy")
- class qibo.backends.abstract.Backend[source]#
- abstract property qubits: list[Union[int, str]] | None#
Return the qubit names of the backend. If
SimulationBackend, return None.
- abstract property connectivity: list[tuple[Union[int, str], Union[int, str]]] | None#
Return the available qubit pairs of the backend. If
SimulationBackend, return None.
- abstract property natives: list[str] | None#
Return the native gates of the backend. If
SimulationBackend, return None.
- abstract set_dtype(dtype: str)[source]#
Set data type of arrays created using the backend.
Note
The data types
float32andfloat64are intended to be used when the circuits to be simulated only contain gates with real-valued matrix representations. Using one of the aforementioned data types with circuits that contain complex-valued matrices will raise a casting error.Note
List of gates that always admit a real-valued matrix representation:
qibo.gates.I,qibo.gates.X,qibo.gates.Z,qibo.gates.H,qibo.gates.Align,qibo.gates.RY,qibo.gates.CNOT,qibo.gates.CZ,qibo.gates.CRY,qibo.gates.SWAP,qibo.gates.FSWAP,qibo.gates.GIVENS,qibo.gates.RBS,qibo.gates.TOFFOLI,qibo.gates.CCZ, andqibo.gates.FanOut.Note
The following parametrized gates can have real-valued matrix representations depending on the values of their parameters:
qibo.gates.RX,qibo.gates.RZ,qibo.gates.U1,qibo.gates.U2,qibo.gates.U3,qibo.gates.CRX,qibo.gates.CRZ,qibo.gates.CU1,qibo.gates.CU2,qibo.gates.CU3,qibo.gates.fSim,qibo.gates.GeneralizedfSim,qibo.gates.RXX,qibo.gates.RYY,qibo.gates.RZZ,qibo.gates.RZX, andqibo.gates.GeneralizedRBS.- Parameters:
dtype (str) – the options are the following:
complex128,complex64,float64, andfloat32.
- abstract set_device(device: str)[source]#
Set simulation device.
- Parameters:
device (str) – Device such as ‘/CPU:0’, ‘/GPU:0’, etc.
- abstract set_threads(nthreads: int)[source]#
Set number of threads for CPU simulation.
- Parameters:
nthreads (int) – Number of threads.
- abstract cast(x, dtype=None, copy: bool = False)[source]#
Cast an object as the array type of the current backend.
- Parameters:
x – Object to cast to array.
dtype (str or type, optional) – data type of
xafter casting. Options are"complex128","complex64","float64", or"float32". IfNone, defaults toBackend.dtype. Defaults toNone.copy (bool, optional) – If
Truea copy of the object is created in memory. Defaults toFalse.
- abstract compile(func)[source]#
Compile the given method.
Available only for the tensorflow backend.
- abstract zero_state(nqubits: int)[source]#
Generate \(|000 \cdots 0 \rangle\) state vector as an array.
- abstract zero_density_matrix(nqubits: int)[source]#
Generate \(|000\cdots0\rangle\langle000\cdots0|\) density matrix as an array.
- abstract identity_density_matrix(nqubits: int, normalize: bool = True)[source]#
Generate density matrix
\[\rho = \frac{1}{2^\text{nqubits}} \, \sum_{k=0}^{2^\text{nqubits} - 1} \, |k \rangle \langle k|\]if
normalize=True. Ifnormalize=False, returns the unnormalized Identity matrix, which is equivalent tonumpy.eye().
- abstract plus_state(nqubits: int)[source]#
Generate \(|+++\cdots+\rangle\) state vector as an array.
- abstract plus_density_matrix(nqubits: int)[source]#
Generate \(|+++\cdots+\rangle\langle+++\cdots+|\) density matrix as an array.
- abstract matrix(gate: qibo.gates.abstract.Gate)[source]#
Convert a
qibo.gates.Gateto the corresponding matrix.
- abstract matrix_parametrized(gate: qibo.gates.abstract.Gate)[source]#
Equivalent to
qibo.backends.abstract.Backend.matrix()for parametrized gates.
- abstract apply_gate_density_matrix(gate, state, nqubits: int)[source]#
Apply a gate to density matrix.
- abstract apply_gate_half_density_matrix(gate, state, nqubits: int)[source]#
Apply a gate to one side of the density matrix.
- abstract apply_channel_density_matrix(channel, state, nqubits: int)[source]#
Apply a channel to density matrix.
- abstract collapse_state(state, qubits, shot, nqubits: int, normalize: bool = True)[source]#
Collapse state vector according to measurement shot.
- abstract collapse_density_matrix(state, qubits, shot, nqubits: int, normalize: bool = True)[source]#
Collapse density matrix according to measurement shot.
- abstract reset_error_density_matrix(gate, state, nqubits: int)[source]#
Apply reset error to density matrix.
- abstract thermal_error_density_matrix(gate, state, nqubits: int)[source]#
Apply thermal relaxation error to density matrix.
- abstract execute_circuit(circuit, initial_state=None, nshots: int = None)[source]#
Execute a
qibo.models.circuit.Circuit.
- abstract execute_circuits(circuits, initial_states=None, nshots: int = None)[source]#
Execute multiple
qibo.models.circuit.Circuitin parallel.
- abstract execute_circuit_repeated(circuit: qibo.models.circuit.Circuit, nshots: int, initial_state=None)[source]#
Execute a
qibo.models.circuit.Circuitmultiple times.Useful for noise simulation using state vectors or for simulating gates controlled by measurement outcomes.
- abstract execute_distributed_circuit(circuit, initial_state=None, nshots: int = None)[source]#
Execute a
qibo.models.circuit.Circuitusing multiple GPUs.
- expectation_observable_dense(circuit: Circuit, observable: ndarray)[source]#
Compute the expectation value of a generic dense hamiltonian starting from the state.
- expectation_diagonal_observable_dense_from_samples(circuit: Circuit, observable: ndarray, nqubits: int, nshots: int, qubit_map: Tuple[int, ...] | None = None) float[source]#
Compute the expectation value of a dense Hamiltonian diagonal in a defined basis starting from the samples (measured in the same basis).
- Parameters:
circuit (
qibo.models.circuit.Circuit) – the circuit to calculate the expectation value from.observable (ndarray) – the (diagonal) matrix corresponding to the observable.
nqubits (int) – the number of qubits of the observable.
nshots (int) – how many shots to execute the circuit with.
qubit_map (Tuple[int, ...], optional) – optional qubits reordering.
- Returns:
The calculated expectation value.
- Return type:
- expectation_diagonal_observable_symbolic_from_samples(circuit: Circuit, nqubits: int, terms_qubits: List[Tuple[int, ...]], terms_coefficients: List[float], nshots: int, qubit_map: Tuple[int, ...] | List[int] | None = None) float[source]#
Compute the expectation value of a symbolic observable diagonal in the computational basis, starting from the samples.
- Parameters:
circuit (
qibo.models.circuit.Circuit) – the circuit to calculate the expectation value from.nqubits (int) – number of qubits of the observable.
terms_qubits (List[Tuple[int, ...]]) – the qubits each term of the (diagonal) symbolic observable is acting on.
terms_coefficients (List[float]) – the coefficient of each term of the (diagonal) symbolic observable.
constant (float) – the constant term of the observable. Defaults to
0..nshots (int) – how many shots to execute the circuit with.
qubit_map (Tuple[int, ...]) – custom qubit ordering.
- Returns:
The calculated expectation value.
- Return type:
- expectation_observable_symbolic_from_samples(circuit, diagonal_terms_coefficients: List[List[float]], diagonal_terms_observables: List[List[str]], diagonal_terms_qubits: List[List[Tuple[int, ...]]], nqubits: int, constant: float, nshots: int) float[source]#
Compute the expectation value of a general symbolic observable defined by groups of terms that can be diagonalized simultaneously, starting from the samples.
- Parameters:
circuit (Circuit) – the circuit to calculate the expectation value from.
diagonal_terms_coefficients (List[float]) – the coefficients of each term of the (diagonal) symbolic observable.
diagonal_terms_observables (List[List[str]]) – the lists of strings defining the observables for each group of terms, e.g.
[['IXZ', 'YII'], ['IYZ', 'XIZ']].diagonal_terms_qubits (List[Tuple[int, ...]]) – the qubits each term of the groups is acting on, e.g.
[[(0,1,2), (1,3)], [(2,1,3), (2,4)]].nqubits (int) – number of qubits of the observable.
constant (float) – the constant term of the observable.
nshots (int) – how many shots to execute the circuit with.
- Returns:
The calculated expectation value.
- Return type:
- expectation_observable_symbolic(circuit: Circuit, terms: List[str], term_qubits: List[Tuple[int, ...]], term_coefficients: List[float], nqubits: int)[source]#
Compute the expectation value of a general symbolic observable that is a sum of terms.
In particular, each term of the observable is contracted with the corresponding subspace defined by the qubits it acts on.
- Parameters:
circuit (
qibo.models.circuit.Circuit) – the circuit to calculate the expectation value from.terms (List[str]) – the lists of strings defining the observables for each term, e.g.
['ZXZ', 'YI', 'IYZ', 'X'].term_coefficients (List[float]) – the coefficients of each term.
term_qubits (List[Tuple[int, ...]]) – the qubits each term is acting on, e.g.
[(0,1,2), (1,3), (2,1,3), (4,)].nqubits (int) – number of qubits of the observable.
- Returns:
The calculated expectation value.
- Return type:
- abstract calculate_symbolic(state, nqubits: int, decimals: int = 5, cutoff: float = 1e-10, max_terms: int = 20)[source]#
Dirac representation of a state vector.
- abstract calculate_symbolic_density_matrix(state, nqubits: int, decimals: int = 5, cutoff: float = 1e-10, max_terms: int = 20)[source]#
Dirac representation of a density matrix.
- abstract calculate_probabilities(state, qubits, nqubits: int)[source]#
Calculate probabilities given a state vector.
- abstract calculate_probabilities_density_matrix(state, qubits, nqubits: int)[source]#
Calculate probabilities given a density matrix.
- abstract sample_shots(probabilities, nshots: int)[source]#
Sample measurement shots according to a probability distribution.
- abstract samples_to_binary(samples, nqubits: int)[source]#
Convert samples from decimal representation to binary.
- abstract samples_to_decimal(samples, nqubits: int)[source]#
Convert samples from binary representation to decimal.
- abstract sample_frequencies(probabilities, nshots: int)[source]#
Sample measurement frequencies according to a probability distribution.
- abstract calculate_vector_norm(state, order: int | float | str = 2)[source]#
Calculate norm of an \(1\)-dimensional array.
For specifications on possible values of the parameter
orderfor thetensorflowbackend, please refer to tensorflow.norm. For all other backends, please refer to numpy.linalg.norm.
- abstract calculate_matrix_norm(state, order: int | float | str = 'nuc')[source]#
Calculate norm of a \(2\)-dimensional array.
Default is the
nuclearnorm. Iforder="nuc", it returns the nuclear norm ofstate, assumingstateis Hermitian (also known as trace norm). For specifications on the other possible values of the parameterorderfor thetensorflowbackend, please refer to tensorflow.norm. For all other backends, please refer to numpy.linalg.norm.
- abstract calculate_overlap_density_matrix(state1, state2)[source]#
Calculate overlap of two density matrices.
- abstract calculate_eigenvalues(matrix, k: int = 6, hermitian: bool = True)[source]#
Calculate eigenvalues of a matrix.
- abstract calculate_eigenvectors(matrix, k: int = 6, hermitian: bool = True)[source]#
Calculate eigenvectors of a matrix.
- abstract calculate_expectation_state(hamiltonian, state, normalize: bool)[source]#
Calculate expectation value of a state vector given the observable matrix.
- abstract calculate_expectation_density_matrix(hamiltonian, state, normalize: bool)[source]#
Calculate expectation value of a density matrix given the observable matrix.
- abstract calculate_matrix_exp(matrix, phase: float | int | complex = 1, eigenvectors=None, eigenvalues=None)[source]#
Calculate the exponential \(e^{\theta \, A}\) of a matrix \(A\) and
phase\(\theta\).If the eigenvectors and eigenvalues are given the matrix diagonalization is used for exponentiation.
- abstract calculate_matrix_log(matrix, base: float | int = 2, eigenvectors=None, eigenvalues=None)[source]#
Calculate the logarithm \(\log_{b}(A)\) with a
base\(b\) of a matrix \(A\).If the eigenvectors and eigenvalues are given the matrix diagonalization is used for exponentiation.
- abstract calculate_matrix_power(matrix, power: float | int, precision_singularity: float = 1e-14)[source]#
Calculate the (fractional)
power\(\alpha\) ofmatrix\(A\), i.e. \(A^{\alpha}\).Note
For the
pytorchbackend, this method relies on a copy of the original tensor. This may break the gradient flow. For the GPU backends (i.e.cupyandcuquantum), this method falls back to CPU wheneverpoweris not an integer.
- abstract calculate_matrix_sqrt(matrix, precision_singularity: float = 1e-14)[source]#
Calculate the square root of
matrix\(A\), i.e. \(A^{1/2}\).Note
For the
pytorchbackend, this method relies on a copy of the original tensor. This may break the gradient flow. For the GPU backends (i.e.cupyandcuquantum), this method falls back to CPU.
Clifford Simulation#
A special backend in qibo supports the simulation of Clifford circuits.
This qibo.backends.clifford.CliffordBackend backend implements the phase-space formalism
introduced in https://arxiv.org/abs/quant-ph/0406196 to efficiently simulate gate
application and measurements sampling in the stabilizers state representation.
The execution of a circuit through this backend creates a
qibo.quantum_info.clifford.Clifford object that gives access to the final measured
samples through the qibo.quantum_info.clifford.Clifford.samples() method,
similarly to qibo.result.CircuitResult.
The probabilities and frequencies are computed starting from the samples by the
qibo.quantum_info.clifford.Clifford.frequencies() and
qibo.quantum_info.clifford.Clifford.probabilities() methods.
It is also possible to recover the standard state representation with the
qibo.quantum_info.clifford.Clifford.state() method.
Note, however, that this process is inefficient as it involves the construction of all the
stabilizers starting from the generators encoded inside the symplectic matrix.
As for the other backends, the Clifford backend can be set with
import qibo
qibo.set_backend("clifford", platform="numpy")
by specifying the engine used for calculation, if not provided the current backend is used
import qibo
# setting numpy as the global backend
qibo.set_backend("numpy")
# the clifford backend will use the numpy backend as engine
backend = qibo.backends.CliffordBackend()
Alternatively, a Clifford circuit can also be executed starting from the qibo.quantum_info.clifford.Clifford object
from qibo.quantum_info import Clifford, random_clifford
nqubits = 2
circuit = random_clifford(nqubits)
result = Clifford.from_circuit(circuit)
- class qibo.backends.clifford.CliffordBackend(engine=None)[source]#
Backend for the simulation of Clifford circuits following Aaronson & Gottesman (2004).
:param
qibo.backends.abstract.Backend: Backend used for the calculation.- cast(x, dtype=None, copy: bool = False)[source]#
Cast an object as the array type of the current backend.
- Parameters:
x – Object to cast to array.
dtype (optional) – data type of the array or tensor. If
None, defaults to the default data type of the current backend. Defaults toNone.copy (bool, optional) – If
Truea copy of the object is created in memory. Defaults toFalse.
- zero_state(nqubits: int, i_phase=False)[source]#
Construct the zero state :math`ket{00…00}`.
- Parameters:
- Returns:
Symplectic matrix for the zero state.
- Return type:
ndarray
- apply_unitary(gate, symplectic_matrix, nqubits)[source]#
Apply a unitary gate to a symplectic matrix following Dehaene & Moor (2003).
- execute_circuit(circuit, initial_state=None, nshots: int = 1000)[source]#
Execute a Clifford circuits.
- Parameters:
circuit (
qibo.models.circuit.Circuit) – Input circuit.initial_state (ndarray, optional) – The
symplectic_matrixof the initial state. IfNone, defaults to the zero state. Defaults toNone.nshots (int, optional) – Number of shots to perform if
circuithas measurements. Defaults to \(10^{3}\).
- Returns:
Object storing to the final results.
- Return type:
- execute_circuit_repeated(circuit, nshots: int = 1000, initial_state=None)[source]#
Execute a Clifford circuits
nshotstimes.This is used for all the simulations that involve repeated execution. For instance when collapsing measurement or noise channels are present.
- Parameters:
circuit (
qibo.models.circuit.Circuit) – input circuit.initial_state (ndarray, optional) – Symplectic_matrix of the initial state. If
None, defaults toqibo.backends.clifford.CliffordBackend.zero_state(). Defaults toNone.nshots (int, optional) – Number of times to repeat the execution. Defaults to \(1000\).
- Returns:
Object storing to the final results.
- Return type:
- sample_shots(state, qubits: tuple | list, nqubits: int, nshots: int, collapse: bool = False)[source]#
Sample shots by measuring selected
qubitsin symplectic matrix of astate.- Parameters:
state (ndarray) – symplectic matrix from which to sample shots from.
qubits – (tuple or list): qubits to measure.
nqubits (int) – total number of qubits of the state.
nshots (int) – number of shots to sample.
collapse (bool, optional) – If
Truethe input state is going to be collapsed with the last shot. Defaults toFalse.
- Returns:
Samples shots.
- Return type:
(ndarray)
- symplectic_matrix_to_generators(symplectic_matrix, return_array: bool = False)[source]#
Extract the stabilizers and destabilizers generators from symplectic matrix.
- Parameters:
symplectic_matrix (ndarray) – The input symplectic_matrix.
return_array (bool, optional) – If
Truereturns the generators asndarrays. IfFalse, generators are returned as strings. Defaults toFalse.
- Returns:
Extracted generators and their corresponding phases, respectively.
- Return type:
Simulation of Hamming-weight-preserving circuits#
This specialised backend in qibo supports the fast simulation of
Hamming-weight-preserving circuits.
Given a quantum state that only contains non-zero amplitudes associated with computational basis
states of Hamming weight \(k\), the qibo.backends.hamming_weight.HammingWeightBackend works with
a compressed representation of quantum states that is restricted to the subspace
with fixed Hamming weight \(k\).
The dimension of this subspace is \(d = \binom{n}{k}\),
where \(n\) is the total number of qubits.
As for the other backends, the Hamming-weight backend can be set by specifying the engine used for calculation, i.e.
from qibo import set_backend
set_backend("hamming_weight", platform="numpy")
If not provided, the current global backend is used:
from qibo import set_backend
from qibo.backends import HammingWeightBackend
# setting numpy as the global backend
set_backend("numpy")
# the Hamming-weight backend will use the numpy backend as engine
backend = HammingWeightBackend()
A Hamming-weight-preserving circuit with Hamming weight \(k\) can be executed as the following example:
from qibo import Circuit, gates, set_backend
from qibo.backends import HammingWeightBackend
backend = HammingWeightBackend()
nqubits = 4
circuit = Circuit(nqubits)
circuit.add(gates.SWAP(0, 1))
result = backend.execute_circuit(circuit, weight=2)
# the above execution is equivalent to the following
# that uses the global backend and the ``weight`` kwarg
#
# set_backend("hamming_weight", platform="numpy")
# result = circuit(weight=2)
- class qibo.backends.hamming_weight.HammingWeightBackend(engine=None)[source]#
Dynamically create a HammingWeightBackend class based on the selected backend.
The results of execution of a circuit through this backend creates a
qibo.quantum_info.hamming_weight.HammingWeightResult
object that gives access to the final state through the
qibo.quantum_info.hamming_weight.HammingWeightResult.state() method.
The probabilities are computed by the
qibo.quantum_info.hamming_weight.HammingWeightResult.probabilities() method.
If there are no measurements in the circuit or the number of shots is \(0\),
they are calculated from the statevector.
Otherwise, they are calculated from the samples.
The final measured samples and frequencies are accessible, respectively, through the
qibo.quantum_info.hamming_weight.HammingWeightResult.samples() and the
qibo.quantum_info.hamming_weight.HammingWeightResult.frequencies() methods.
It is also possible to recover the standard state representation with the
qibo.quantum_info.hamming_weight.HammingWeightResult.full_state() method.
Note, however, that this process is inefficient as it involves the construction of
a statevector with size exponential in the number of qubits.
- class qibo.quantum_info.hamming_weight.HammingWeightResult(state, weight: int, nqubits: int, measurements=None, nshots: int = 1000, engine=None)[source]#
Object storing the results of a circuit execution with the
qibo.backends.hamming_weight.HammingWeightBackend.- Parameters:
state (ndarray) – statevector with a fixed Hamming weight. The dimension of the state is \(d = \binom{n}{k}\), where \(n\) is the number of qubits and \(k\) is the Hamming weight. The components of the state are ordered in lexicographical order.
weight (int) – Hamming weight of
state.nqubits (int) – number of qubits of
state.measurements (list, optional) – list of measurements gates
qibo.gates.M. Defaults toNone.nshots (int, optional) – number of shots used for sampling the measurements. Defaults to \(1000\).
engine (str, optional) – engine to use in the execution of the
qibo.backends.HammingWeightBackend. It accepts"numpy","numba","cupy", and"cuquantum". IfNone, defaults to the corresponding engine from the current backend. Defaults toNone.
- symbolic(decimals: int = 5, cutoff: float = 1e-10, max_terms: int = 20)[source]#
Dirac notation representation of the state in the computational basis.
- Parameters:
decimals (int, optional) – Number of decimals for the amplitudes. Defaults to \(5\).
cutoff (float, optional) – Amplitudes with absolute value smaller than the cutoff are ignored from the representation. Defaults to \(1e-10\).
max_terms (int, optional) – Maximum number of terms to print. If the state contains more terms they will be ignored. Defaults to \(20\).
- Returns:
String representing the state in the computational basis.
- Return type:
- full_state()[source]#
Tensor representation of
statein the entire computational basis.Note
This method is inefficient in runtime and memory for a large number of qubits.
- probabilities(qubits: list | set | None = None)[source]#
Calculate the probabilities of the measured qubits.
If the number of shots is \(0\) or no measurements were performed, the probabilities are calculated from the statevector. Otherwise, the probabilities are calculated from the samples.
- samples(binary: bool = True, registers: bool = False)[source]#
Returns raw measurement samples.
- Parameters:
- Returns:
- If
binaryisTrue samples are returned in binary form as a tensor of shape
(nshots, n_measured_qubits).- If
binaryisFalse samples are returned in decimal form as a tensor of shape
(nshots,).- If
registersisTrue samples are returned in a
dictwhere the keys are the register names and the values are the samples tensors for each register.- If
registersisFalse a single tensor is returned which contains samples from all the measured qubits, independently of their registers.
- If
- frequencies(binary: bool = True, registers: bool = False)[source]#
Return the frequencies of measured samples.
- Parameters:
- Returns:
A
collections.Counterwhere the keys are the observed values and the values the corresponding frequencies, that is the number of times each measured value/bitstring appears.- If
binaryisTrue the keys of the
collections.Counterare in binary form, as strings of \(0\) and :math`1`.- If
binaryisFalse the keys of the
collections.Counterare integers.- If
registersisTrue a dict of
collections.Counteris returned where keys are the name of each register.- If
registersisFalse a single
collections.Counteris returned which contains samples from all the measured qubits, independently of their registers.
- If
Cloud Backends#
Additional backends that support the remote execution of quantum circuits through cloud service providers, such as IBM and QRC-TII, are provided by the optional qibo plugin qibo-cloud-backends. For more information please refer to the official documentation.