Quantum Convolutional Neural Network Classifier

Code at: https://github.com/qiboteam/qibo/tree/master/examples/qcnn_classifier. Please note that scikit-learn is needed to visualize the results.

Problem overview

This tutorial implements a simple Quantum Convolutional Neural Network (QCNN), which is a translationally invariant algorithm analogous to the classical convolutional neural network. This example demonstrates the use of the QCNN as a quantum classifier, which attempts to classify ground states of a translationally invariant quantum system, the transverse field Ising model, based on whether they are in the ordered or disordered phase. The (randomized) statevector data provided are those of a 4-qubit system. Accompanying each state is a label: +1 (disordered phase) or -1 (ordered phase).

Through the sequential reduction of entanglement, this network is able to perform classification from the final measurement of a single qubit.

Workflow of QCNN model:

Schematic of QCNN model:

Convolutional layer for 4 qubits as an example:

Pooling layer for 4 qubits as an example:

where in the above, \(R(\theta_{i,j,k}) = RZ(\theta_k) RY(\theta_j) RX(\theta_i)\):

\(U_{q_a, q_b}(\theta_{i,j,k}) = RXX(\theta_k) RYY(\theta_j) RZZ(\theta_i)\) is a two-qubit gate acting on qubits \(q_a\) and \(q_b\):

and \(R^{\dagger}(\theta_{i,j,k}) = RX(-\theta_i) RY(-\theta_j) RZ(-\theta_k)\):

How to use the QCNN class

For more details on the QuantumCNN class, please refer to the documentation. Here we recall some of the necessary arguments when instantiating a QuantumCNN object: - nqubits (int): number of quantum bits. It should be larger than 2 for the model to make sense. - nlayers (int): number of layers of the QCNN variational ansatz. - nclasses (int): number of classes of the training set (default=2). - params: list to initialise the variational parameters (default=None).

After creating the object, one can proceed to train the model. For this, the QuantumCNN.minimize method can be used with the following arguments (refer to the documentation for more details)” - init_theta: list or numpy.array with the angles to be used in the circuit - data: the training data - labels: numpy.array containing the labels for the training data - nshots (int):number of runs of the circuit during the sampling process (default=10000) - method (string): str ‘classical optimizer for the minimization’. All methods from scipy.optimize.minmize are suported (default=‘Powell’).

QCNN Demo

Include necessary packages:

import numpy as np
import random
from sklearn import metrics

import qibo
from qibo.models.qcnn import QuantumCNN

qibo.set_backend("numpy")

[Qibo 0.1.13|INFO|2023-05-15 17:25:59]: Using numpy backend on /CPU:0

Load the provided data (ground states of 4-qubit TFIM in data folder) and labels:

data = np.load('nqubits_4_data_shuffled_no0.npy')
labels = np.load('nqubits_4_labels_shuffled_no0.npy')
labels = np.transpose(np.array([labels])) # restructure to required array format

Structure of data and labels are like:

data[-2:]

array([[0.52745364+0.j, 0.19856967+0.j, 0.19856967+0.j, 0.16507377+0.j,
        0.19856967+0.j, 0.09784837+0.j, 0.16507377+0.j, 0.19856967+0.j,
        0.19856967+0.j, 0.16507377+0.j, 0.09784837+0.j, 0.19856967+0.j,
        0.16507377+0.j, 0.19856967+0.j, 0.19856967+0.j, 0.52745364+0.j],
       [0.67109214+0.j, 0.10384038+0.j, 0.10384038+0.j, 0.05351362+0.j,
        0.10384038+0.j, 0.02786792+0.j, 0.05351362+0.j, 0.10384038+0.j,
        0.10384038+0.j, 0.05351362+0.j, 0.02786792+0.j, 0.10384038+0.j,
        0.05351362+0.j, 0.10384038+0.j, 0.10384038+0.j, 0.67109214+0.j]])

labels[-2:]

array([[ 1.],
       [-1.]])

Split the data into training/test set in the ratio 60:40

split_ind = int(len(data) * 0.6)
train_data = data[:split_ind]
test_data = data[split_ind:]

train_labels = labels[:split_ind]
test_labels = labels[split_ind:]

Initialize the QuantumCNN class:

test = QuantumCNN(nqubits=4, nlayers=1, nclasses=2)
testcircuit = test._circuit
testcircuit.draw()

q0:     ─RX─RY─RZ─RZZ─RYY─RXX─RX─RY─RZ──────────────────────────────────────── ...
q1:     ─RX─RY─RZ─RZZ─RYY─RXX─RX─RY─RZ─────────────RX─RY─RZ──────────RZZ─RYY─R ...
q2:     ──────────────────────RX─RY─RZ─RZZ─RYY─RXX─RX─RY─RZ─RX─RY─RZ─RZZ─RYY─R ...
q3:     ──────────────────────RX─RY─RZ─RZZ─RYY─RXX─RX─RY─RZ─────────────────── ...

q0: ... ───RX─RY─RZ─RZZ─RYY─RXX─RX─RY─RZ─RX─RY─RZ─o───────────────────────
q1: ... XX─RX─RY─RZ─|───|───|─────────────────────|─RX─RY─RZ─o────────────
q2: ... XX─RX─RY─RZ─|───|───|───RX─RY─RZ──────────X─RZ─RY─RX─|────────────
q3: ... ───RX─RY─RZ─RZZ─RYY─RXX─RX─RY─RZ────────────RX─RY─RZ─X─RZ─RY─RX─M─

draw() is used to visualize the pre-constructed circuit based on input parameters for class initialization.

Initialize model parameters:

testbias = np.zeros(test.measured_qubits)
testangles = [random.uniform(0,2*np.pi) for i in range(21*2)]
init_theta = np.concatenate((testbias, testangles))

Train model with optimize parameters (automatically updates model with optimized paramters at the end of training):

result = test.minimize(init_theta, data=train_data, labels=labels, nshots=10000, method='Powell')

Alternatively, update model with optimized parameters from previous training:

saved_result_60 = (0.2026119742575817, np.array([ -0.06559061,   3.62881221,   2.39850148,   3.02493711,
         0.91498683,   3.25517842,   0.0759049 ,   3.46049453,
         3.04395784,   1.55681424,   2.3665245 ,   0.40291846,
         5.67310744,   2.27615444,   5.23403537,   0.46053411,
         0.69228362,   2.2308165 ,   0.53323661,   4.52157388,
         5.31194656,  18.23511858,  -1.90754635,  14.30577217,
        10.75135972,  19.16001316,  12.27582746,   7.47476354,
        23.38129141,  60.29771502,  10.02946377,  17.83945879,
        15.22732248,  12.34666584,   1.52634649,   1.90621517,
        12.71554053, -13.56379057,  34.04591253, -11.56450878,
        10.95038782,   3.30640208,   9.67270071]))

test.set_circuit_params(angles=saved_result_60[1], has_bias=True)

Generate predictions from optimized model:

predictions = []
for n in range(len(test_data)):
    predictions.append(test.predict(test_data[n], nshots=10000)[0])

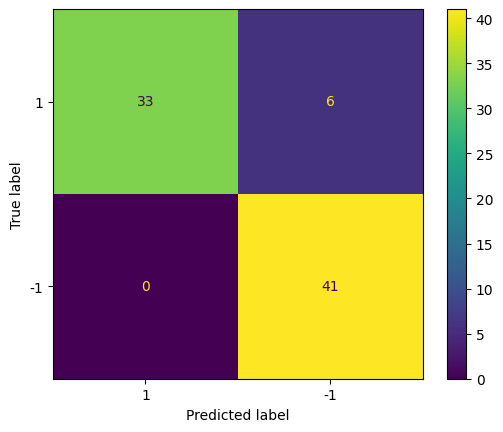
Visualize results via confusion matrix and accuracy:

actual = [np.sign(test_labels) for test_labels in test_labels]
predicted = [np.sign(prediction) for prediction in predictions]

confusion_matrix = metrics.confusion_matrix(actual, predicted)

cm_display = metrics.ConfusionMatrixDisplay(confusion_matrix = confusion_matrix, display_labels = [1, -1])

cm_display.plot()

<sklearn.metrics._plot.confusion_matrix.ConfusionMatrixDisplay at 0x7efd85b82200>

test.Accuracy(test_labels,predictions)

0.925