Quantum Fourier Iterative Amplitude Estimation#
Code at: https://github.com/qiboteam/qibo/tree/master/examples/qfiae.
Based on the paper arXiv:2305.01686
Problem overview#
This tutorial implements an example of the application of the Quantum Fourier Iterative Amplitude Estimation (QFIAE) method, which allows to perform Quantum Monte Carlo integration of any one-dimensional function \(f(x)\).
The QFIAE algorithm functioning is the following:
The function we want to integrate \(f(x)\), the probability distribution \(p(x)\) and the limits of the integral \(x_{min}\), \(x_{max}\) are defined
A Quantum Neural Network (QNN) is employed to fit the function \(f(x)\) using a linear ansatz of the following form:
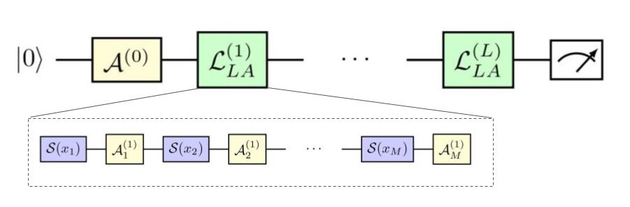
where \(\mathcal{L}^{(i)}\) is the i-th layer, that for the one-dimensional case is composed of the trainable gates:
and the encoding gate:
Now, as demonstrated in arXiv:2008.08605 the expectation value of this quantum model corresponds to a universal 1-D Fourier series:
The Fourier coefficients of the quantum circuit that fits the function \(f(x)\) are extracted using discrete Fourier transform
The Iterative Quantum Amplitude Estimation (IQAE) model of qibo, which corresponds with the following quantum circuit:
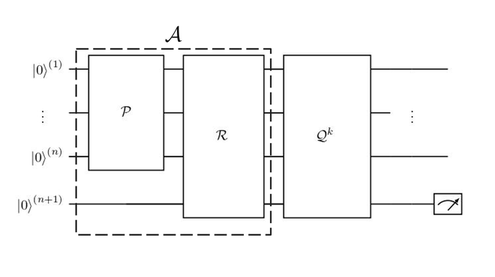
is used to estimate the integral of each trigonometric piece, \(\sin(\omega_i x)\) or \(\cos(\omega_j x)\), of the Fourier series.
The integrals obtained are summed with their corresponding coefficients to derive the final integral result.
A summary of the workflow of the algorithm is the following: 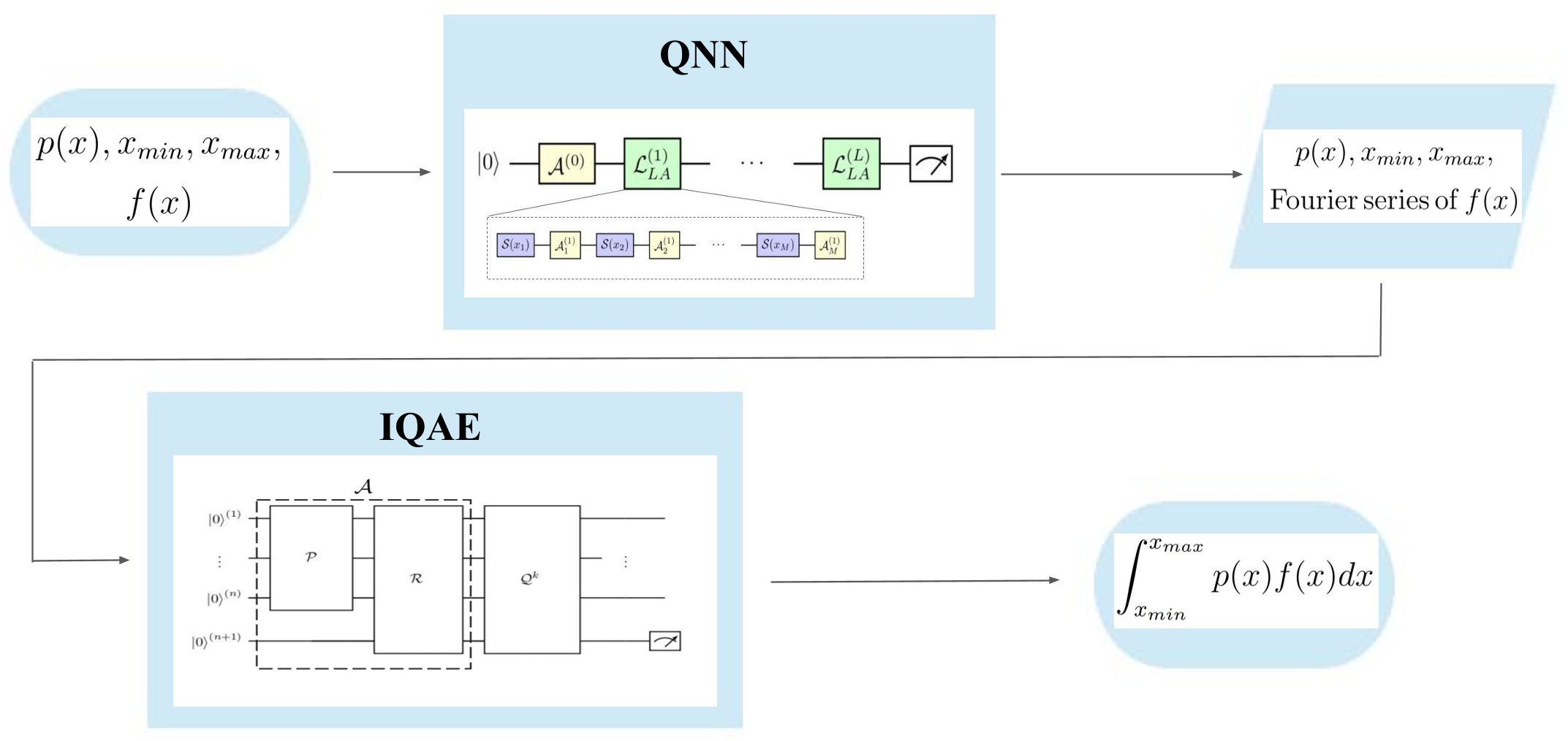
QFIAE Demo#
Let’s define the problem:
We are interested in computing the following example integral:
so the easiest way to define our problem variables would be:
\(x_{min}\): \(0\)
\(x_{max}\): \(1\)
\(p(x)\): \(dx\)
\(f(x)\): \(1+x^2\)
Code#
First, we must decide the variables for our problem.
Regarding the definition of the problem:
x_min_int: the lower limit of the problem integral.x_max_int: the upper limit of the problem integral.
Regarding the QNN:
nlayers: number of layers of the QNN.nepochs: number of epochs, i.e. iterations of the AdamDescent Optimizer.loss_treshold: value of the desired loss function’s treshold.learning_rate: learning rate of the AdamDescent Optimizer.nbatches: number of batches in which divide the dataset.ndata_points: number of data points to define \(f(x)\).x_max_fit: upper limit of the function we are going to fit.x_min_fit: lower limit of the function we are going to fit.
Regarding the IQAE:
nqubits: number of qubits decided to build the good state in the IQAE algorithm.alpha: confidence level, the target probability is 1 -alpha, has values between 0 and 1.epsilon: target precision for estimation target \(a\), has values between 0 and 0.5.nshots: number of shots used to perform IQAE.method_iqae: statistical method employed by IQAE. It will be chernoff or beta.
Regardind the results:
qfiae_integral: estimated value of the integral using QFIAE.iae_error: statistical uncertainty in the integral estimation due to IQAE.
Include necessary packages:
[1]:
import numpy as np
from qibo import Circuit, gates
from qibo.models.iqae import IQAE
1. Defining \(f(x)\), \(x_{min}\), \(x_{max}\)#
[2]:
def f(x):
"""Target function f(x) = 1 + x ^ 2"""
y = 1 + x ** 2
return y
x_min_int = 0
x_max_int = 1
2. Defining and training the QNN#
We import the QNN: vqregressor_linear_ansatz, which is a modified version of the vqregressor found at https://github.com/qiboteam/qibo/tree/master/examples/vqregressor. In our modified version, we replace the ansatz function used in the original implementation with the one we have previously defined.
[3]:
from vqregressor_linear_ansatz import VQRegressor_linear_ansatz
We define the parameters of the QNN
[4]:
# Note that the chosen number of layers is intentionally larger than necessary to fit the function.
# This configuration ensures high accuracy while keeping a reasonable number of epochs.
nlayers = 10
nepochs = 100
loss_treshold = 10^-4
learning_rate = 0.05
nbatches = 1
ndata_points = 200
# Note they can be different than x_min,x_max, but [x_max,x_min] ⊆ [x_max_fit,x_min_fit]
x_max_fit = 1
x_min_fit = -1
[5]:
np.random.seed(27)
vqr = VQRegressor_linear_ansatz(layers=nlayers,
ndata=ndata_points,
function=f, xmax=x_max_fit,
xmin=x_min_fit)
# With the selected configuration, the training usually takes around 30'
vqr.train_with_psr(
epochs=nepochs,
learning_rate=learning_rate,
batches=nbatches,
J_treshold=loss_treshold,
)
vqr.show_predictions("Predictions of the QNN after training", False)
[Qibo 0.1.16|INFO|2023-07-31 08:50:42]: Using qibojit (numba) backend on /CPU:0
Iteration 1 epoch 1 | loss: 0.7513285431118756
Iteration 2 epoch 2 | loss: 0.49078195900193
Iteration 3 epoch 3 | loss: 0.25449817735514246
Iteration 4 epoch 4 | loss: 0.1246609331106105
Iteration 5 epoch 5 | loss: 0.0656780490580047
Iteration 6 epoch 6 | loss: 0.033157170041590786
Iteration 7 epoch 7 | loss: 0.021080634318318345
Iteration 8 epoch 8 | loss: 0.02302933284076279
Iteration 9 epoch 9 | loss: 0.02804566383739096
Iteration 10 epoch 10 | loss: 0.02993298809989462
Iteration 11 epoch 11 | loss: 0.02809272996633005
Iteration 12 epoch 12 | loss: 0.024260018563301875
Iteration 13 epoch 13 | loss: 0.020466737677239978
Iteration 14 epoch 14 | loss: 0.017961154451515637
Iteration 15 epoch 15 | loss: 0.01635525503721851
Iteration 16 epoch 16 | loss: 0.013824870329752614
Iteration 17 epoch 17 | loss: 0.009480363571353416
Iteration 18 epoch 18 | loss: 0.005428317914456559
Iteration 19 epoch 19 | loss: 0.004747379983842302
Iteration 20 epoch 20 | loss: 0.007261736229780217
Iteration 21 epoch 21 | loss: 0.008972805823541971
Iteration 22 epoch 22 | loss: 0.006995705828705413
Iteration 23 epoch 23 | loss: 0.0031234835775331904
Iteration 24 epoch 24 | loss: 0.0010645149525778657
Iteration 25 epoch 25 | loss: 0.001660608449799947
Iteration 26 epoch 26 | loss: 0.0024468184819136764
Iteration 27 epoch 27 | loss: 0.0019337945857293712
Iteration 28 epoch 28 | loss: 0.0012357754610404163
Iteration 29 epoch 29 | loss: 0.0013015455646036862
Iteration 30 epoch 30 | loss: 0.0016682446926897167
Iteration 31 epoch 31 | loss: 0.0016495496176469587
Iteration 32 epoch 32 | loss: 0.0012520977035885572
Iteration 33 epoch 33 | loss: 0.0009722650541584987
Iteration 34 epoch 34 | loss: 0.0010738639185073821
Iteration 35 epoch 35 | loss: 0.001237623835436679
Iteration 36 epoch 36 | loss: 0.001079914927835038
Iteration 37 epoch 37 | loss: 0.0008087925855009583
Iteration 38 epoch 38 | loss: 0.0008412140573143836
Iteration 39 epoch 39 | loss: 0.0010243360494146807
Iteration 40 epoch 40 | loss: 0.0009260517614442422
Iteration 41 epoch 41 | loss: 0.0006083674444202678
Iteration 42 epoch 42 | loss: 0.00048552087540479593
Iteration 43 epoch 43 | loss: 0.0006110987021632932
Iteration 44 epoch 44 | loss: 0.0006559683517174265
Iteration 45 epoch 45 | loss: 0.0005150053878726019
Iteration 46 epoch 46 | loss: 0.0004114721142009153
Iteration 47 epoch 47 | loss: 0.0004471177670137205
Iteration 48 epoch 48 | loss: 0.0004770075457458069
Iteration 49 epoch 49 | loss: 0.00040857499834427296
Iteration 50 epoch 50 | loss: 0.00033020904524591827
Iteration 51 epoch 51 | loss: 0.0003179087176282798
Iteration 52 epoch 52 | loss: 0.00032425348191094495
Iteration 53 epoch 53 | loss: 0.0003081269055732997
Iteration 54 epoch 54 | loss: 0.00029739364175727137
Iteration 55 epoch 55 | loss: 0.0002972067254557964
Iteration 56 epoch 56 | loss: 0.0002790839752707141
Iteration 57 epoch 57 | loss: 0.000250994009314296
Iteration 58 epoch 58 | loss: 0.00024068099758678817
Iteration 59 epoch 59 | loss: 0.00024012049242896222
Iteration 60 epoch 60 | loss: 0.00023072309010057932
Iteration 61 epoch 61 | loss: 0.0002204255806400206
Iteration 62 epoch 62 | loss: 0.00021693211012467254
Iteration 63 epoch 63 | loss: 0.00021032053408251615
Iteration 64 epoch 64 | loss: 0.00019814302410227347
Iteration 65 epoch 65 | loss: 0.00018970104609909337
Iteration 66 epoch 66 | loss: 0.0001849409887409433
Iteration 67 epoch 67 | loss: 0.000178175085771177
Iteration 68 epoch 68 | loss: 0.00017235266528996997
Iteration 69 epoch 69 | loss: 0.00016920670127216307
Iteration 70 epoch 70 | loss: 0.00016352665275946328
Iteration 71 epoch 71 | loss: 0.0001558330982688153
Iteration 72 epoch 72 | loss: 0.00015122871287318634
Iteration 73 epoch 73 | loss: 0.0001481650541488665
Iteration 74 epoch 74 | loss: 0.0001435783238101642
Iteration 75 epoch 75 | loss: 0.000139808928386417
Iteration 76 epoch 76 | loss: 0.00013763074842478883
Iteration 77 epoch 77 | loss: 0.00013405673992693997
Iteration 78 epoch 78 | loss: 0.00012925759824435786
Iteration 79 epoch 79 | loss: 0.00012568131156775818
Iteration 80 epoch 80 | loss: 0.000122960138626043
Iteration 81 epoch 81 | loss: 0.00012002635696736961
Iteration 82 epoch 82 | loss: 0.00011738809629738198
Iteration 83 epoch 83 | loss: 0.00011504380983272437
Iteration 84 epoch 84 | loss: 0.00011252787350936655
Iteration 85 epoch 85 | loss: 0.00011014441030141236
Iteration 86 epoch 86 | loss: 0.00010794102346639878
Iteration 87 epoch 87 | loss: 0.00010557841843900766
Iteration 88 epoch 88 | loss: 0.00010325318195926471
Iteration 89 epoch 89 | loss: 0.00010112572290540777
Iteration 90 epoch 90 | loss: 9.901680049760298e-05
Iteration 91 epoch 91 | loss: 9.702508371139033e-05
Iteration 92 epoch 92 | loss: 9.525568074239291e-05
Iteration 93 epoch 93 | loss: 9.354329673964097e-05
Iteration 94 epoch 94 | loss: 9.188064428852769e-05
Iteration 95 epoch 95 | loss: 9.032782168927708e-05
Iteration 96 epoch 96 | loss: 8.881823164035069e-05
Iteration 97 epoch 97 | loss: 8.739132343365943e-05
Iteration 98 epoch 98 | loss: 8.607781395924396e-05
Iteration 99 epoch 99 | loss: 8.477887801842459e-05
Iteration 100 epoch 100 | loss: 8.350302085692635e-05
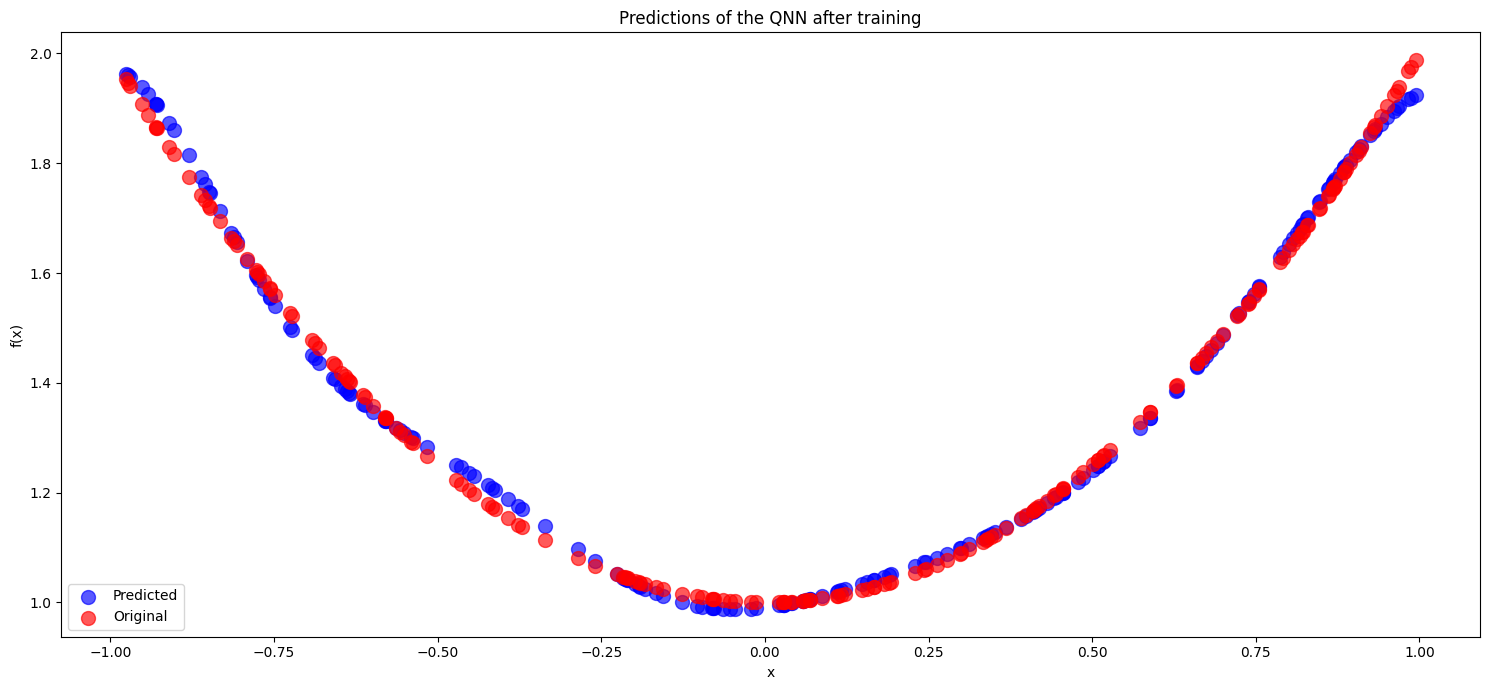
3. Obtaining the Fourier series from the QNN#
[6]:
# We import the qibo function that obtains the Fourier series out of a
# quantum circuit that returns an expectation value
from qibo.models.utils import fourier_coefficients
# We get the optimized quantum circuit and the normalized Fourier coefficients
quantum_circuit_optimized = vqr.one_prediction
normalized_coeffs = fourier_coefficients(quantum_circuit_optimized,
n_inputs=1, degree=nlayers, lowpass_filter=True)
# We obtain the non-normalized coeffs
coeffs = normalized_coeffs * vqr.norm
Let’s see how they look like
[7]:
print(coeffs)
[ 9.91228857e-01+0.j -9.14152432e-04-0.04336848j
3.40828521e-01-0.02305663j -1.77033953e-01+0.00110917j
-3.63049787e-01+0.12160816j 7.33018369e-02-0.05831041j
2.28576955e-01-0.1387953j -2.13031210e-03+0.16034618j
-1.57394048e-01-0.03133756j 5.23539080e-02-0.02270211j
5.30676569e-03-0.00145169j 5.30676569e-03+0.00145169j
5.23539080e-02+0.02270211j -1.57394048e-01+0.03133756j
-2.13031210e-03-0.16034618j 2.28576955e-01+0.1387953j
7.33018369e-02+0.05831041j -3.63049787e-01-0.12160816j
-1.77033953e-01-0.00110917j 3.40828521e-01+0.02305663j
-9.14152432e-04+0.04336848j]
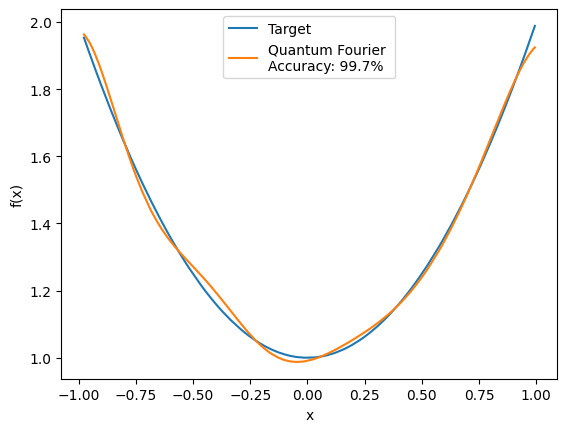
Now we check that Fourier series obtained it’s correct and also fits the function
[8]:
# We import some functions to obtain the Fourier series from the coefficients and to plot these results
from utils_qfiae import fourier_series, plot_data_fourier
# We plot the original function and the Fourier approximation
y_fourier = fourier_series(coeffs, vqr.features)
plot_fourier, accuracy_qnn = plot_data_fourier(vqr.labels * vqr.norm, vqr.features, y_fourier)
4. Integrating every trigonometric piece#
First we should rewrite the Fourier coefficients in a way that will be easy to integrate the trigonometric functions Sine and Cosine
[9]:
# We import some functions to convert exponential-like Fourier coefficients into trigonometric-like and to
# convert this trigonometric coeffs into an array that provides insight about if we get a Sine or a Cosine
from utils_qfiae import exp_fourier_to_trig, trig_to_final_array
trig_coeffs = exp_fourier_to_trig(coeffs)
fourier_array = trig_to_final_array(trig_coeffs)
Let’s visualize what we have and note that in the first columnn 0 stands for Cosine and 1 stands for Sine, in the second column we have the frequencies and in the third one the coefficients
[10]:
print(fourier_array)
[[ 0.00000000e+00 0.00000000e+00 9.91228857e-01]
[ 0.00000000e+00 1.00000000e+00 -1.82830486e-03]
[ 0.00000000e+00 2.00000000e+00 6.81657041e-01]
[ 0.00000000e+00 3.00000000e+00 -3.54067907e-01]
[ 0.00000000e+00 4.00000000e+00 -7.26099574e-01]
[ 0.00000000e+00 5.00000000e+00 1.46603674e-01]
[ 0.00000000e+00 6.00000000e+00 4.57153911e-01]
[ 0.00000000e+00 7.00000000e+00 -4.26062419e-03]
[ 0.00000000e+00 8.00000000e+00 -3.14788097e-01]
[ 0.00000000e+00 9.00000000e+00 1.04707816e-01]
[ 0.00000000e+00 1.00000000e+01 1.06135314e-02]
[ 1.00000000e+00 1.00000000e+00 8.67369616e-02]
[ 1.00000000e+00 2.00000000e+00 4.61132575e-02]
[ 1.00000000e+00 3.00000000e+00 -2.21834947e-03]
[ 1.00000000e+00 4.00000000e+00 -2.43216317e-01]
[ 1.00000000e+00 5.00000000e+00 1.16620823e-01]
[ 1.00000000e+00 6.00000000e+00 2.77590597e-01]
[ 1.00000000e+00 7.00000000e+00 -3.20692363e-01]
[ 1.00000000e+00 8.00000000e+00 6.26751169e-02]
[ 1.00000000e+00 9.00000000e+00 4.54042108e-02]
[ 1.00000000e+00 1.00000000e+01 2.90337531e-03]]
Before implementeing the IQAE model, we should define the quantum circuits \(\mathcal{A}\) and \(\mathcal{Q}\).
The circuit \(\mathcal{A}\) is defined as:
where \(a\in[0,1]\) is the parameter to be estimated, while \(|\tilde{\psi}_1\rangle\) and \(|\tilde{\psi}_0\rangle\) are the \(n\)-qubit good and bad states, respectively.
From a more practical point of view, this circuit can be decomposed in two pieces:
where \(\mathcal{I}_1\) is the identity matrix acting over the last qubit.
So, to get \(\mathcal{A}\) we have to define the operator \(\mathcal{P}\), which encodes the probability distribution \(p(x)\), and the operator \(\mathcal{R}\), which encodes the function we are going to integrate, \(\sin(x)^2\), into the interval \([b_{min},b_{max}]\)
[11]:
def operator_p(circ, list_of_qubits):
"""Generating the uniform probability distribution p(x)=1/2^n"""
for qubit in list_of_qubits:
circ.add(gates.H(q=qubit))
def operator_r(circ, list_of_qubits, qubit_to_measure, b_max, b_min):
"""Encoding the function Sin(x)^2 to be integrated in the interval [b_min,b_max]"""
number_of_qubits = qubit_to_measure
circ.add(
gates.RY(q=qubit_to_measure, theta=(b_max - b_min) / 2 ** number_of_qubits + 2 * b_min)
)
for qubit in list_of_qubits:
circ.add(
gates.CRY(qubit, qubit_to_measure,
(b_max - b_min) / 2 ** (number_of_qubits-qubit-1))
)
Then, the circuit \(\mathcal{A}\) will be:
[12]:
def create_circuit_a(n_qubits, b_max, b_min):
"""Creation of circuit A"""
circuit_a = Circuit(n_qubits + 1)
list_of_qubits = list(range(n_qubits))
operator_p(circuit_a, list_of_qubits)
operator_r(circuit_a, list_of_qubits, n_qubits, b_max, b_min)
return circuit_a
Let’s see how the circuit A looks like for \(n_{qubits}\)=4
[13]:
circuit_a_prob = create_circuit_a(n_qubits = 4,b_max = x_max_int, b_min = x_min_int)
circuit_a_prob.draw()
q0: ─H──o───────────
q1: ─H──|──o────────
q2: ─H──|──|──o─────
q3: ─H──|──|──|──o──
q4: ─RY─RY─RY─RY─RY─
On the other hand, the circuit \(\mathcal{Q}\) is defined as:
where the operator \(S_0\) tags with a negative sign the \(|0\rangle_{n+1}\) state and does nothing to the other states, and the operator \(S_\chi\) changes the sign to the good state, i.e. \(S_\chi |\tilde{\psi}_1\rangle|1\rangle=-|\tilde{\psi}_1\rangle|1\rangle\).
So, let’s define \(S_0\) and \(S_\chi\) to get \(\mathcal{Q}\):
[14]:
def operator_s_0(circ, qubit_to_measure):
"""Tagging with a negative sign any state different to |0>_{n+1}. Note that this is
the opposite of what S_0 is supposed to do. The explanation is that the operator
here defined has absorbed the minus sign in \mathcal{Q}."""
circ.add(gates.Z(q = qubit_to_measure))
def operator_s_chi(circ, qubit_to_measure):
"""Computing reflection operator (I - 2|0><0|)"""
number_of_qubits = qubit_to_measure
list_of_qubits = list(range(number_of_qubits))
for qubit in list_of_qubits:
circ.add(gates.X(q = qubit))
circ.add(gates.X(q=qubit_to_measure))
circ.add(gates.Z(qubit_to_measure).controlled_by(*range(0,qubit_to_measure)))
circ.add(gates.X(q=qubit_to_measure))
for qubit in list_of_qubits:
circ.add(gates.X(q = qubit))
Then the circuit \(\mathcal{Q}\) will be:
[15]:
def create_circuit_q(n_qubits, circuit_a):
"""Creation of circuit Q"""
circuit_q = Circuit(n_qubits + 1)
operator_s_0(circuit_q, n_qubits)
circuit_q.add(circuit_a.invert().on_qubits(
*range(0, n_qubits + 1, 1)))
operator_s_chi(circuit_q, n_qubits)
circuit_q.add(circuit_a.on_qubits(
*range(0, n_qubits + 1, 1)))
return circuit_q
Let’s see how the circuit Q looks like for \(n_{qubits}\)=4
[16]:
create_circuit_q(n_qubits=4,circuit_a=circuit_a_prob).draw()
q0: ────────────o──H──X─o─X─H──o───────────
q1: ─────────o──|──H──X─o─X─H──|──o────────
q2: ──────o──|──|──H──X─o─X─H──|──|──o─────
q3: ───o──|──|──|──H──X─o─X─H──|──|──|──o──
q4: ─Z─RY─RY─RY─RY─RY─X─Z─X─RY─RY─RY─RY─RY─
Since we already have the circuits \(\mathcal{A}\) and \(\mathcal{Q}\), we can proceed to execute the IQAE model.
But first let’s do the last transformation of the Fourier coefficients
[17]:
from utils_qfiae import coeffs_array_to_class
coeffs_class = coeffs_array_to_class(fourier_array)
Then, we will create the following function that will integrate each sine and cosine and then sum every term to obtain the final Monte Carlo integral.
To create this integrator we will use the following mathematical properties:
\begin{equation} \frac{1}{x_{min}-x_{min}}\int_{x_{min}}^{x_{max}}dx\sin(x \omega/2)^2=\frac{1}{b_{max}-b_{min}} \int_{b_{min}}^{b_{max}}dx\sin(x)^2, \tag{1} \end{equation}
if \(b_{max}=x_{max}\omega / 2\) and \(b_{min}=x_{min} \omega / 2\).
\begin{equation} \sin(x) = \cos (x - \pi/2) \tag{2} \end{equation}
\begin{equation} \cos(x) = 1 - 2 \sin(x/2) ^ 2 \tag{3} \end{equation}
[18]:
def qfiae_integrator(coeffs_f, x_max, x_min, nbit, shots, alpha, epsilon, method):
"""Takes the Fourier coefficients of the desired function and calculates the integral of the function
in the specified interval."""
mc_integral = 0
error_iqae = 0
if coeffs_f[0].angle == 0:
mc_integral += coeffs_f[0].coeff * (x_max - x_min)
for n in range(1,len(coeffs_f)):
angle = coeffs_f[n].angle
if coeffs_f[n].function == 0: # cosine
# Here we use Eq.(1)
a_circuit = create_circuit_a(n_qubits=nbit,
b_max=x_max * angle / 2,
b_min=x_min * angle / 2)
if coeffs_f[n].function == 1: # sine
# Here we use Eq.(2)
a_circuit = create_circuit_a(n_qubits=nbit,
b_max=x_max * angle / 2 - np.pi / 4,
b_min=x_min * angle / 2 - np.pi / 4)
q_circuit = create_circuit_q(n_qubits=nbit, circuit_a=a_circuit)
result = IQAE(a_circuit, q_circuit, alpha, epsilon, n_shots=shots, method=method).execute()
a_estimated = result.estimation
# This `a_estimated` corresponds to the integral of the right part of Eq.(1)
error = result.epsilon_estimated
# Here we use Eq.(3) and multiply the result by (x_max - x_min) to get rid of the normalization
mc_integral += (1 - 2 * a_estimated) * coeffs_f[n].coeff * (x_max - x_min)
error_iqae += (2 * abs(coeffs_f[n].coeff) * error * (x_max - x_min))**2
return mc_integral , np.sqrt(error_iqae)
Finally, we define the parameters for the IQAE model and execute the qfiae_integrator function
[19]:
nqubits = 4
nshots = 1024
alpha = 0.05
epsilon = 0.005
method_iqae = "chernoff"
qfiae_integral, iae_error = qfiae_integrator(coeffs_class, x_max=x_max_int, x_min=x_min_int,
nbit=nqubits, shots=nshots, alpha=alpha,
epsilon=epsilon, method=method_iqae)
Once the QFIAE algorithm has been performed we can visualize and compare the results with the ones obtained by classical calculation
[20]:
from scipy.integrate import quad
classical_integral, classical_error = quad(f, x_min_int, x_max_int)
print("The result obtained with QFIAE is", qfiae_integral,
" ± ", iae_error)
print("The result obtained with classical numerical integration is",
classical_integral, " ± ", classical_error)
The result obtained with QFIAE is 1.3368772283309165 ± 0.00781780414187758
The result obtained with classical numerical integration is 1.3333333333333333 ± 1.4802973661668752e-14