Variational Quantum Classifier#
Code at: https://github.com/qiboteam/qibo/tree/master/examples/variational_classifier.
Problem overview#
We want to perform a supervised classification task with a variational quantum classifer. The classifier is trained to minimize a local loss function given by the quadratic deviation of the classifier’s predictions from the actual labels of the examples in the training set. A variational quantum circuit is employed to perform the classification.
Implementing the solution#
The standard iris data set is chosen for the classification task. It consists of 150 4-dimensional data vectors containing the length and widht of the sepals and petals of individuals from three different species of plants (Iris setosa, Iris versicolor, Iris virginica). We associate one computational-basis state to each of the classes (|00>, |01>, |10>) in the subspace of measured qubits, and we employ the following architecture for the ansatz:
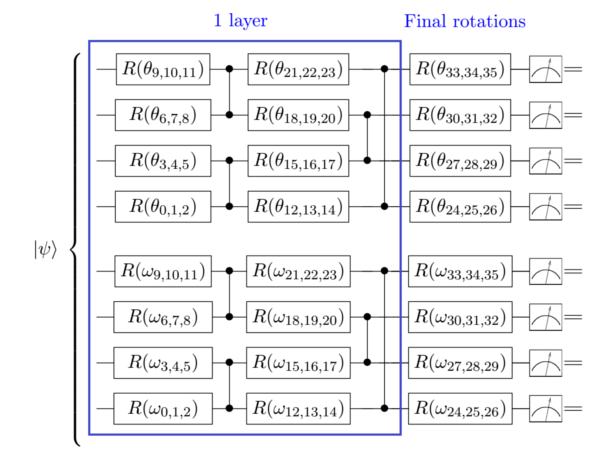
where R stands for Ry rotations (if RxRzRx=False) or RxRzRx rotations.
How to run an example#
To run a particular instance of the problem, we have to set up the initial arguments:
nclases(int): number of classes of the training set (default=3)nqubits(int): number of quantum bits. It must be larger than 1 (default=4)nlayers(int): number of ansatz layers. (default=5)nshots(int): number of shots used when sampling the circuit. (default=100000)training(flag): if True, actual training occurs. If False, pre-computed optimal values are employed, with default nqubits and nlayers. (default=False)RxRzRx(flag): if True, RxRzRx rotations are used in the ansatz. If False, Ry are employed instead. (default=False)method(string): classical optimization method, supported by scipy.optimize.minimize. (default=’Powell’)
To run an example with the optimal values obtained for 4 qubits and 5 layers, you should execute the following command:
python main.py
To run an example with different values, and actually train the classifier, type for example:
python main.py --nqubits 4 --nlayers 5 --nshots 100000 --training
Note that nclases must be 3 and cannot be changed in this example, because we are classifing the Iris data set.
Results#
The classification accuracy for the training and test sets is found to be around 70% and 73%, respectively.