Frequency vs flux experiments#

In this section we show how to run experiments to study the flux dependence.

Flux-tunable transmons#

It can be shown for flux-tunable transmons that applying an external flux \(\Phi\) induces to a detuning on the transmon frequency [13]. By applying short flux pulses it is possible to tune the transmon frequency in order of GHz, which leads to several applications including quantum logical gates.

The transmon frequency as a function of the external flux can be expressed as [1]

(1)#\[f_q(\Phi) = \Bigg( f_q^{\text{max}} + \frac{E_C}{h} \Bigg) \sqrt[4]{d^2 + (1-d^2)\cos^2\Big( \pi \frac{\Phi}{\Phi_0}\Big)} - \frac{E_C}{h} \,\]

where \(f_{\text{max}} = ( \sqrt{8 E_C E_J} - E_C) / h\) is the maximum qubit frequency, \(d\) is the junctions asymmetry, \(E_C\) is the charging energy, \(E_J\) is the Josephson energy and \(\Phi_0 = h / (2e)\) is the flux quanta.

The resonator detuning in the transmon regime \(E_J \gg E_C\) can be computed as

\[f_r(\Phi) = f_r^{\text{bare}} + g_0^2 \frac{\sqrt[4]{d^2 + (1-d^2)\cos^2\Big( \pi \frac{\Phi}{\Phi_0}\Big)}}{f_r^{\text{bare}} - f_q(\Phi)} \,\]

where \(f_r^{\text{bare}}\) is the bare frequency of the resonator and \(g_0^2\) is the coupling between the transmon and the resonator.

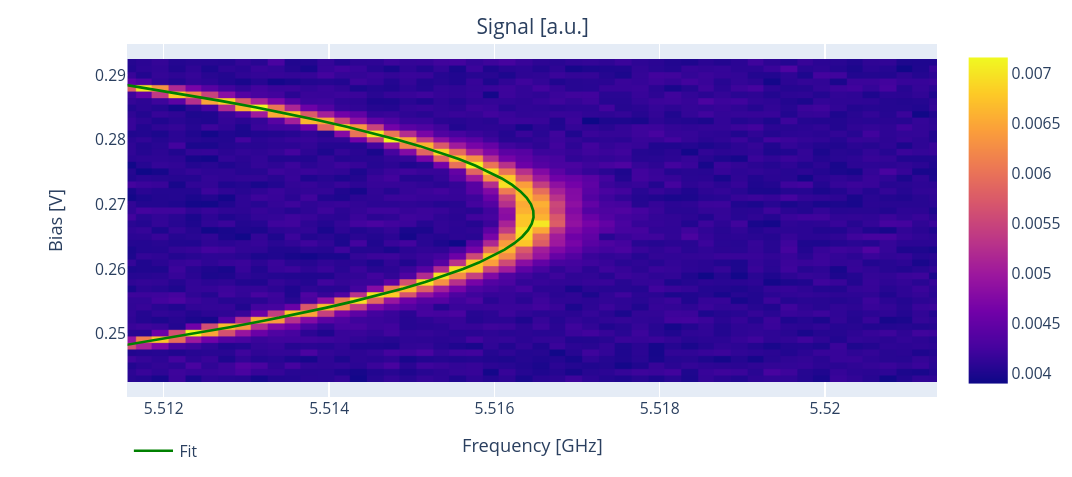
In Qibocal we provide two experiments to measure and fit the curves described by the two equations above. To measure the qubit detuning a 2D sweep is performed probing the systems at different drive frequencies and at different flux (bias) offset values. For the resonator we perform the same experiment by sweeping the readout frequency instead of the drive frequency.

Qubit flux dependence#

Parameters#

class qibocal.protocols.flux_dependence.qubit_flux_dependence.QubitFluxParameters(freq_width: int, freq_step: int, bias_width: Optional[float] = None, bias_step: Optional[float] = None, drive_amplitude: Optional[float] = None, drive_duration: int = 2000)[source]

QubitFlux runcard inputs.

drive_amplitude: Optional[float] = None: Drive amplitude (optional). If defined, same amplitude will be used in all qubits. Otherwise the default amplitude defined on the platform runcard will be used

drive_duration: int = 2000: Duration of the drive pulse.

bias_step: Optional[float] = None: Bias step for sweep [a.u.].

bias_width: Optional[float] = None: Width for bias sweep [V].

hardware_average: bool = False: By default hardware average will be performed.

freq_width: int: Width for frequency sweep relative to the readout frequency [Hz].

freq_step: int: Frequency step for sweep [Hz].

nshots: int: Number of executions on hardware.

relaxation_time: float: Wait time for the qubit to decohere back to the gnd state.

Example#

A possible runcard to assess how the qubit frequency changes by varying flux is the following:

- id: qubit flux dependence
  operation: qubit_flux
  parameters:
    bias_step: 0.001
    bias_width: 0.05
    drive_amplitude: 0.002
    drive_duration: 4000
    freq_step: 200000
    freq_width: 10000000
    nshots: 1024
    relaxation_time: 20000

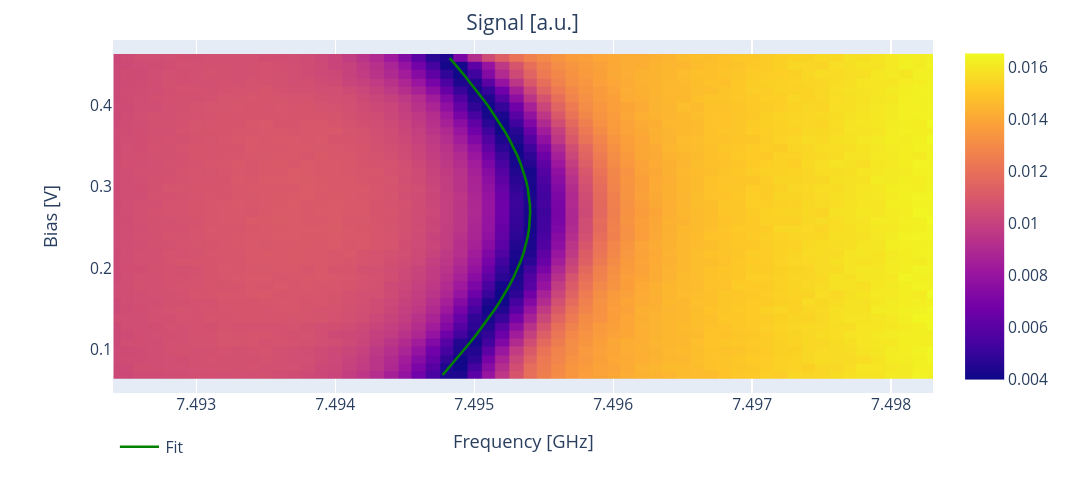
The expected output is the following:

From the acquired data this protocol estimates the flux insensitive point “sweetspot”, which corresponds to the flux value where the frequency is maximed, as well as the drive frequency and the diagonal crosstalk coefficient \(V_{ii}\).

Note

From the cosinusoidal term in the transmon equation (1), it is clear that the sweetspot is not unique. In this protocol, Qibocal returns the sweetspot that is closest to the bias that is in the middle of the swept interval.

Both the sweetspot and the \(C_{ii}\) can be understood by writing the full expression for the flux felt by qubit \(i\) [1]:

\[\Phi_i = \sum_{j} C_{ij} V_j + \Phi_i^{\text{offset}} \,\]

where \(C_{ij}\) is known in the literature as the crosstalk matrix, while \(V_{i}\) is the applied voltage.

Requirements#

Qubit spectroscopies

Resonator flux dependence#

Parameters#

class qibocal.protocols.flux_dependence.resonator_flux_dependence.ResonatorFluxParameters(freq_width: int, freq_step: int, bias_width: Optional[float] = None, bias_step: Optional[float] = None)[source]

ResonatorFlux runcard inputs.

freq_width: int: Width for frequency sweep relative to the readout frequency [Hz].

freq_step: int: Frequency step for sweep [Hz].

bias_width: Optional[float] = None: Width for bias sweep [V].

bias_step: Optional[float] = None: Bias step for sweep [a.u.].

hardware_average: bool = False: By default hardware average will be performed.

nshots: int: Number of executions on hardware.

relaxation_time: float: Wait time for the qubit to decohere back to the gnd state.

Example#

A possible runcard to assess how the resonator frequency changes by varying flux is the following:

- id: resonator flux dependence
  operation: resonator_flux
  parameters:
    bias_step: 0.01
    bias_width: 0.4
    freq_step: 100000
    freq_width: 6000000
    nshots: 2000
    relaxation_time: 1000