Cryoscope experiment#

In this section we show how to run a cryoscope experiment using Qibocal.

The goal of the Cryoscope experiment is to reconstruct the shape of the flux pulse sent to the qubit in order to determine correction for signal distortions. To do this we exploit the dependence of the transition frequency of a transmon qubit on the magnetic flux

(1)#\[f_Q(\Phi_Q)\approx \frac{1}{h} \left( \sqrt{8E_J E_C \left| \cos\left(\pi\frac{\Phi_Q}{\Phi_0}\right) \right|} - E_C \right)\]

where \(E_C\) is the charging energy, \(E_J\) is the sum of the Jospehson energies and \(\Phi_0\) is the flux quantum. The routine implementation follows the description given in [20]:

Cryoscope#

The cryoscope experiment consists of a Ramsey-like experiment where a flux pulse is embedded between the two \(\pi/2\) pulses separated by a fixed time interval \(T\). The first \(\pi /2\) rotation around the \(Y\) axis change the qubit state from \(\ket{0}\) to \(\frac{\ket{0}+\ket{1}}{\sqrt{2}}\); then the flux pulse transforms the qubit state to \(\frac{\ket{0}+e^{i\phi_\tau}\ket{1}}{\sqrt{2}}\) where

(2)#\[\frac{\phi_\tau}{2\pi} = \int_0^T \Delta f_Q(\Phi_{Q,\tau}(t))dt\]

Then the experiment is completed with a \(\pi/2\) rotation either around the \(y\) axis or around the \(x\) axis in order to obtain, respectively the \(\langle Y \rangle\) or \(\langle X \rangle\) component of the Bloch vector. From the \(\langle X \rangle\) and \(\langle Y \rangle\) components of the Bloch vector we can derive the relative phase \(\phi_\tau\) which in turn can be used to computed

\[\Delta f_R \equiv \frac{\phi{\tau+\Delta\tau} - \phi_{\tau}}{2\pi \Delta\tau}\]

and then we can extract an estimate of the effective flux pulse \(\Phi_Q(t)\) on the qubit by inverting (1).

Flux amplitude frequency#

In Qibocal implementation of Cryoscope is necessary to run a flux amplitude-frequency experiment before performing a cryoscope experiment. This auxiliary routine is used determine the coefficients of the quadratic relationship between the qubit frequency and the flux pulse amplitude in the vicinity of the sweetspot.

Parameters#

class qibocal.protocols.flux_amplitude_frequency.FluxAmplitudeFrequencyParameters(amplitude_min: int, amplitude_max: int, amplitude_step: int, duration: float)[source]

FluxAmplitudeFrequency runcard inputs.

amplitude_min: int: Minimum flux pulse amplitude.

amplitude_max: int: Maximum flux amplitude.

amplitude_step: int: Flux pulse amplitude step.

duration: float: Flux pulse duration.

hardware_average: bool = False: By default hardware average will be performed.

nshots: int: Number of executions on hardware.

relaxation_time: float: Wait time for the qubit to decohere back to the gnd state.

Example#

The following is an example of runcard that can be used to acquire the coefficients for the amplitude-frequency relation for the flux pulse

- id: flux amplitude frequency

  operation: flux_amplitude_frequency
  parameters:
    amplitude_max: 0.7
    amplitude_min: 0.0
    amplitude_step: 0.001
    duration: 60
    relaxation_time: 50000

The expected output is the following:

../../_images/flux_amplitude_frequency.png

Parameters#

class qibocal.protocols.two_qubit_interaction.cryoscope.CryoscopeParameters(duration_min: int, duration_max: int, duration_step: int, flux_pulse_amplitude: float, fir: int = 20, unrolling: bool = True)[source]

Cryoscope runcard inputs.

duration_min: int: Minimum flux pulse duration.

duration_max: int: Maximum flux duration start.

duration_step: int: Flux pulse duration step.

flux_pulse_amplitude: float: Flux pulse amplitude.

fir: int = 20: Number of feedforward taps to be optimized after IIR.

unrolling: bool = True

hardware_average: bool = False: By default hardware average will be performed.

nshots: int: Number of executions on hardware.

relaxation_time: float: Wait time for the qubit to decohere back to the gnd state.

Example#

A possible runcard to launch a Cryoscope experiment could be the following:

- id: cryoscope

  operation: cryoscope
  parameters:
    duration_max: 80
    duration_min: 1
    duration_step: 1
    flux_pulse_amplitude: 0.7
    relaxation_time: 50000

The expected output is the following:

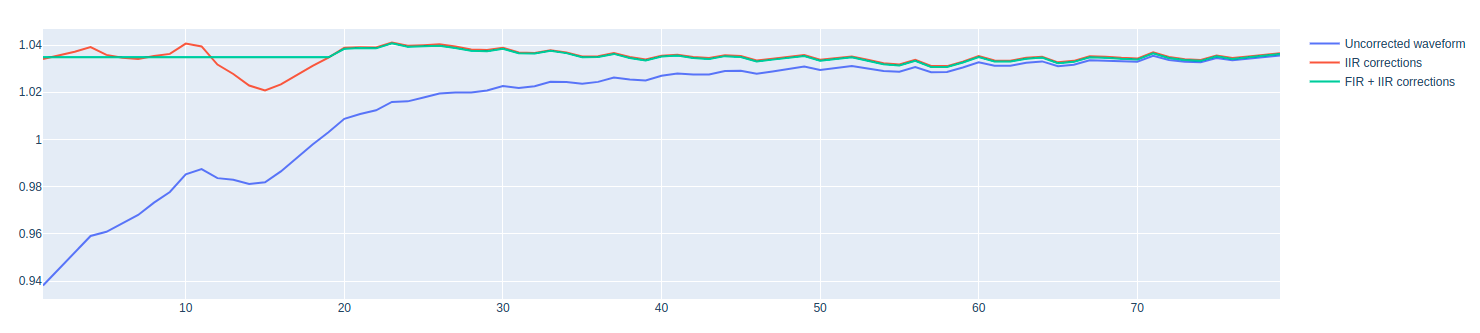
Note

In the case where there are no filters the protocol will compute the FIR and the IIR filters. If the filters are already present the computation of the filters will be skipped and only the reconstructed waveform will be shown.

Requirements#

Single Shot Experiments