Resonator spectroscopy

When calibrating the readout pulse, the first thing to do is finding the resonator frequency. At this frequency we will be able to observe a clear difference in the transmitted signal: if the resonator is a 3D cavity we will observe an amplified signal, while for a 2D resonator we will observe a higher absorption. In both cases, we expect to see a Lorentzian peak (positive for 3D cavity or negative for 2D resonators).

In the experiment, we send a readout pulse with fixed duration and amplitude and, after waiting for the time of flight, we acquire a waveform that we average, obtaining a single point. This experiment is extremely dependent on the amplitude of the pulse.

Since the objective of this experiment is to find the resonator frequency, without any readout optimization (something that we will have to do afterwards), we can fix the duration of the pulse in the order of magnitude of µs. For the amplitude the discussion is slightly more complex and there are several elements to take into consideration:

• higher amplitudes usually correspond to better signal to noise ratio;

• at high amplitudes the signal breaks superconductivity, therefore resonator is not effectively not coupled to the qubit (we talk of bare resonator frequency);

• at intermediate amplitudes the peak could completely disappear and is, in general, not Lorentzian;

• very high amplitudes could damage the components.

The bare resonator frequency can be found setting a large value for the amplitude, e.g.:

Parameters

class qibocal.protocols.resonator_spectroscopy.ResonatorSpectroscopyParameters(freq_width: int, freq_step: int, power_level: Union[PowerLevel, str], amplitude: Optional[float] = None, attenuation: Optional[int] = None, hardware_average: bool = True)

ResonatorSpectroscopy runcard inputs.

freq_width: int

Width for frequency sweep relative to the readout frequency [Hz].

freq_step: int

Frequency step for sweep [Hz].

power_level: Union[PowerLevel, str]

Power regime (low or high). If low the readout frequency will be updated. If high both the readout frequency and the bare resonator frequency will be updated.

amplitude: Optional[float] = None

Readout amplitude (optional). If defined, same amplitude will be used in all qubits. Otherwise the default amplitude defined on the platform runcard will be used

attenuation: Optional[int] = None

Readout attenuation (optional). If defined, same attenuation will be used in all qubits. Otherwise the default attenuation defined on the platform runcard will be used

hardware_average: bool = True

By default hardware average will be performed.

nshots: int

Number of executions on hardware

relaxation_time: float

Wait time for the qubit to decohere back to the gnd state

Example

- id: resonator_spectroscopy high power

  operation: resonator_spectroscopy
  parameters:
      freq_width: 60_000_000
      freq_step: 200_000
      amplitude: 0.6
      power_level: high
      nshots: 1024
      relaxation_time: 100000

Note

The resonator spectroscopy experiment will be performed by computing the average on hardware. If the user wants to retrieve all the shots and perform the average afterwards it can be done by specifying the entry hardware_average: false in the experiment parameters. In this case the fitting procedure will take into account errors and error bands will be included in the plot.

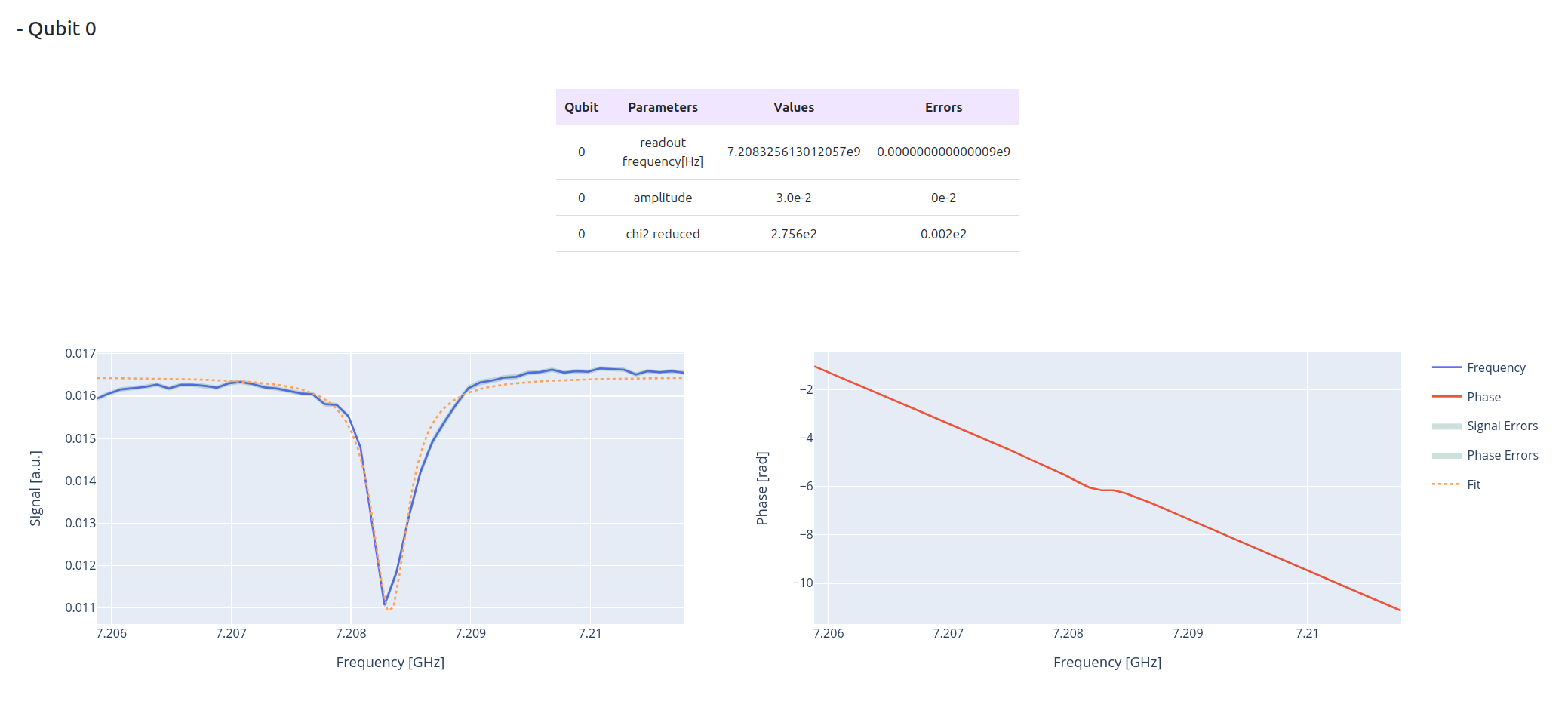
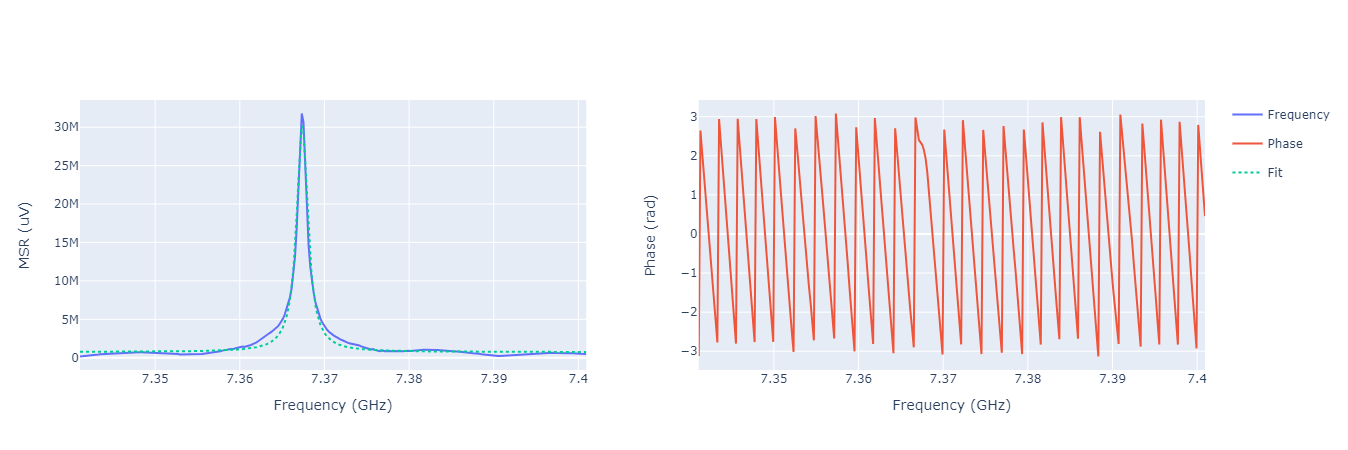
Lowering the amplitude we can see a shift in the peak, e.g.:

Example

- id: resonator_spectroscopy low power

  operation: resonator_spectroscopy
  parameters:
      freq_width: 60_000_000
      freq_step: 200_000
      amplitude: 0.03
      power_level: low
      nshots: 1024
      relaxation_time: 100000

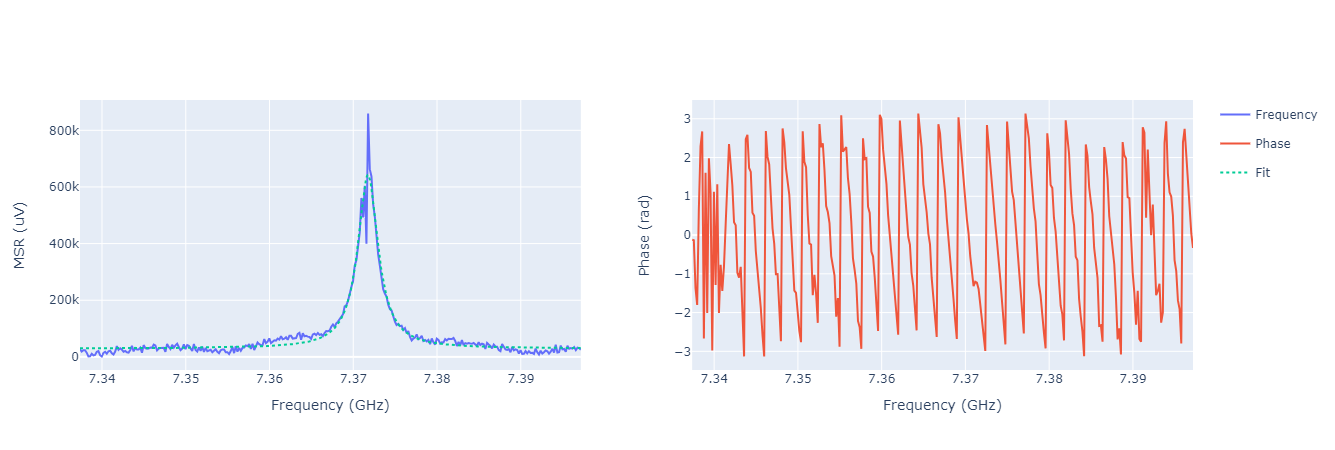
Running the qibocal routines above produces outputs in the reports like the ones shown above. The peaks are Lorentzian. As we can see, at low power the resonator fequency shifts. This is due to the Hamiltonian of the system [3, 11]. Therefore, the dressed resonator frequency is larger than the bare resonator frequency.

Lowering the amplitude value also reduces the height of the peak and increases the noise.

Another parameter connected to the amplitude, is also the relaxation time (in some literature also referred to as repetition duration) and the number of shots. The number of shots represents the number of repetitions of the same experiment (at the same frequency), while the relaxation time is the waiting time between repetitions. A higher number of shots will increase the S/N ratio by averaging the noise, but will also slow down the acquisition. As per the relaxation time, for this experiment in particular we can leave it at zero: since we are not exciting the qubit we do not particularly care about it. However note that, for 3D cavities, we could end up damaging the qubit if we send too much energy over a small period of time so it could be worth to increase the relaxation time. However, some electronics do not support zero relaxation times, therefore a relaxation time greater than zero is a safer choice.

Last but not least, we have to choose which frequencies are probed during the scan: a very wide scan can be useful if nothing is known about the studied resonator, but in general we have at least the design parameters. These are often not exact, but can give an idea of the region to scan (for standard cavities around 7 GHz). Also, a very small step between two subsequent frequency points is not needed and could really slow down the experiment (from seconds to tens of minutes) if chosen incorrectly. Usually, a step of 200 MHz is fine enough.

The resonator frequencies can be then inserted into the platform runcards (in qibolab_platforms_qrc). For example, if we are reading qubit 0:

native_gates:
    single_qubit:
        0: # qubit number
            RX:
                duration: 40
                amplitude: <high_power_amplitude>
                frequency: <high_power_resonator_frequency>
                shape: Gaussian(5)
                type: qd # qubit drive
                relative_start: 0
                phase: 0
            MZ:
                duration: 2000
                amplitude: <low_power_amplitude>
                frequency: <low_power_resonator_frequency>
                shape: Rectangular()
                type: ro # readout
                relative_start: 0
                phase: 0

and also here:

characterization:
    single_qubit:
        0:
            bare_resonator_frequency: <high_power_resonator_frequency>
            readout_frequency: <low_power_resonator_frequency>

Requirements

• Time Of Flight (Readout)