Building your first Quantum Model#
In order to build a Quantum Model you need to define two fundamental ingredients:
the
circuit_structure: a general quantum circuit can be composed of encoding Unitaries and trainable Unitaries. In practice, in Qiboml, we use theEncoderclass to build the encoding layers of our quantum circuits (namely, the operations where we encode external input data), while we leave the user the freedom of constructing any trainable layer using Qibo’sCircuitinterface or by defining custom functions of independent parameters that are combined to produce aCircuit. The set of elements composing the circuit structure can then be provided as a list to the Qiboml quantum models.a
Decoderin charge of decoding the quantum information contained in the final state we get once executing the whole circuit structure.
In the following picture, we showcase a full quantum machine learning pipeline: after defining a custom quantum circuit structure, this is executed on the chosen Qibo backend both for computing predictions and gradients during the optimization.
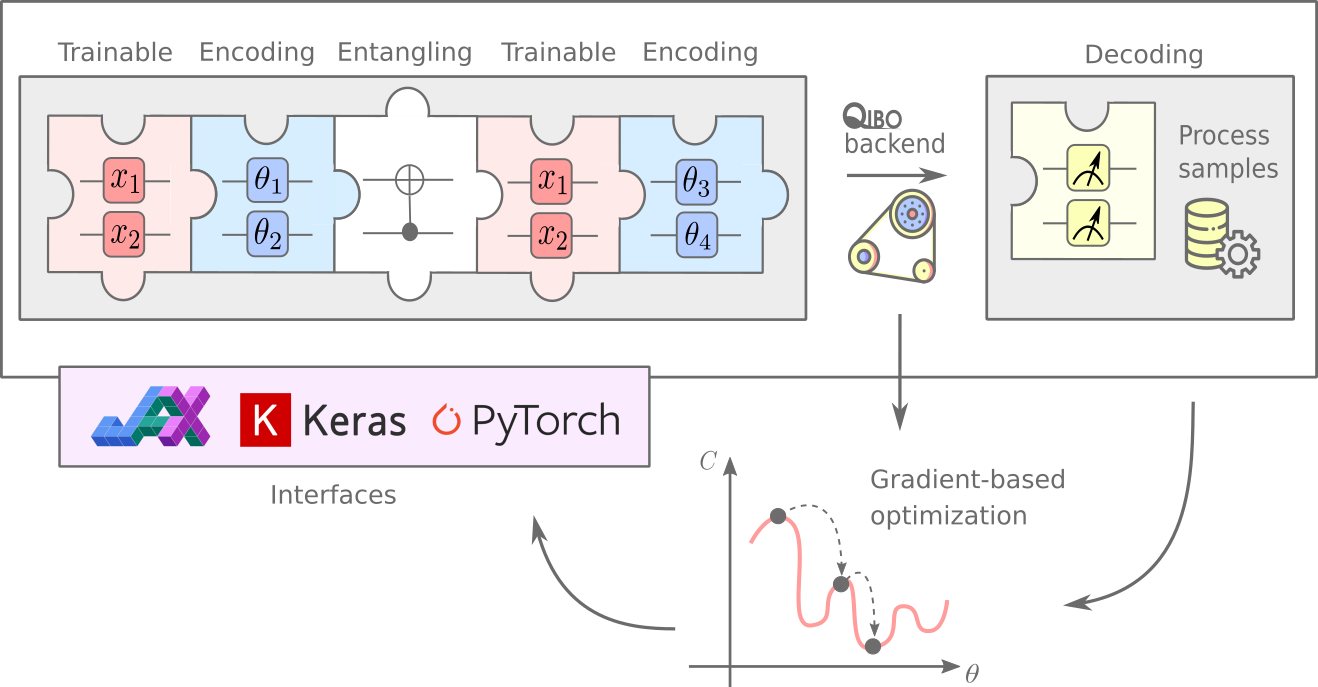
Following this structure, every single evaluation of the model, divided in the steps Encoding -> Circuit Composition -> Execution -> Decoding, takes as input classical data and outputs classical data once again.
In qiboml we provide some standard pre-defined encoding and decoding layers, whereas the trainable part can be delegated to any qibo circuit (some standard quantum circuit ansaetze are available as well). The different pieces can be joined together through a qiboml interface, which exposes a QuantumModel object in one of the popular ML frameworks (such as torch and keras).
Note
We are planning to support trainable encodings, but for now the structure has to be defined by explicitly separating encoding and trainable layers.
Therefore, building a qiboml model is rather immediate. For instance using the torch interface:
import torch
from qibo import Circuit, gates, hamiltonians
from qiboml.models.encoding import PhaseEncoding
from qiboml.models.decoding import Expectation
from qiboml.interfaces.pytorch import QuantumModel
# define the encoding
encoding = PhaseEncoding(nqubits=3)
# define the decoding given an observable
observable = hamiltonians.Z(nqubits=3)
decoding = Expectation(nqubits=3, observable=observable)
# build the computation circuit
circuit = Circuit(3)
circuit.add((gates.RY(i, theta=0.4) for i in range(3)))
circuit.add((gates.RZ(i, theta=0.2) for i in range(3)))
circuit.add((gates.H(i) for i in range(3)))
circuit.add((gates.CNOT(0,1), gates.CNOT(0,2)))
circuit.draw()
# join everything together through the torch interface
quantum_model = QuantumModel(
circuit_structure=[encoding, circuit],
decoding=decoding,
)
# run on some data
data = torch.randn(3)
outputs = quantum_model(data)
Note that the qiboml.interfaces.pytorch.QuantumModel object is a torch.nn.Module, it is thus fully compatible and integrable with the standard torch API. For instance, it can be concatenated to other torch layers through torch.nn.Sequential:
linear = torch.nn.Linear(8, 3)
activation = torch.nn.Tanh()
model = torch.nn.Sequential(
linear,
activation,
quantum_model,
)
outputs = model(torch.randn(8))
and it can be trained using a torch.optim optimizer:
optimizer = torch.optim.Adam(model.parameters())
data = torch.randn(8)
for i in range(10):
target = torch.tensor([[0.5]])
optimizer.zero_grad()
outputs = model(data)
loss = torch.nn.functional.mse_loss(outputs, target)
loss.backward()
optimizer.step()